阶梯水平井产能预测方法
李 苗,李晓平,郭 平
(1.中国石油化工股份有限公司石油勘探开发研究院,北京 100083;2.西南石油大学研究生部,四川 成都 610500;3.西南石油大学油气藏地质及开发工程国家重点实验室,四川 成都 610500)
阶梯水平井产能预测方法
李 苗1,2,李晓平3,郭 平3
(1.中国石油化工股份有限公司石油勘探开发研究院,北京 100083;2.西南石油大学研究生部,四川 成都 610500;3.西南石油大学油气藏地质及开发工程国家重点实验室,四川 成都 610500)
摘要:根据质量守恒原理和动量守恒原理,建立了双台阶水平井筒沿程压降模型。通过比产能指数将井筒中的流动与油藏渗流进行了耦合。模型中油藏渗流计算采用JOSHI稳态流动模型,水平井筒摩擦压降计算考虑了壁面流入的影响。并为所建的模型编制了程序,通过实例计算分析双台阶水平井相关参数对产能的影响,认为对于大井眼、小产能水平井加速度压降可忽略,摩擦压降较小,由水平倾角引起的重力压降对产能有较大影响。本文为油藏工程分析和采油工艺分析建立了一种简单、快捷、有效的阶梯水平井产能预测方法。
关键词:裸眼完井;耦合模型;阶梯水平井;产能预测
阶梯水平井是指在一个井眼中连续完成具有一定高度差的两个或者多个水平井段,形成具有两个或多个台阶的井眼轨迹,用一个井眼开采或者勘探两个或多个层叠状油藏、断块油藏的水平井井型。利用阶梯水平井连续在这两个油层中水平延伸一定长度,节约了重复钻井的投资,增加了单井产量,可取得最佳的开发效果。常用于阶梯式水平井开发的区块具有以下特点:①层叠式或不整合薄油藏;②断块油藏;③上部油层断失或尖灭,存在下部可供开采的油藏[1~3]。
国内外油田关于阶梯水平井钻、完井工艺报道较多,常规水平井势的分布也已有诸多研究。但是阶梯水平井的开发理论研究较少,目前现场应用时仅将阶梯水平井考虑为两个水平井[4]。因此本文在对阶梯水平井生产段进行数学描述的基础上,建立一种快捷、有效的阶梯水平井产能预测方法,可用于钻完井设计、油藏工程分析和采油工艺设计。
1 水平井筒内单相变质量流特性
水平井水平段井筒内的流动具有如下特征:1)存在主流与径向入流两种流动。主流即水平井筒内从指端到根端的轴向流动;径向入流即油藏流体向水平井筒的入流;从水平井筒指端到跟端,流体质量流量逐渐增加,其流动为变质量流。所以加速度压降不再等于零,其影响不能忽略;2)水平井筒内的流动存在压力损失,导致沿井筒的压力分布不均。压力损失包括摩擦损失、加速损失、流体混合损失以及势能损失。3)水平井筒内的流动与油藏渗流存在流动耦合。径向流入的流量大小会影响水平井筒内压力分布及压降大小,而井筒内的压力分布会反过来影响从油藏径向流入井筒的流量大小,因而油藏内的渗流与水平井筒内的流动还是耦合的[5]。故建立水平井筒内压降计算模型必须考虑这些流动特性。
2 阶梯水平井生产段空间特征
将阶梯水平井生产段划分为3段(图1):上部水平段Ⅰ,下部水平段Ⅱ和连接段Ⅲ。并对模型做以下基本假设:
1)薄层油藏为均质、各向同性地层;
2)水平段均采用裸眼完井方式,且连接段Ⅲ对产能没有贡献;
3)阶梯水平井所钻遇的薄层油藏为边界封闭(包括定压封闭)油藏;
4)上部水平段和下部水平段都于所钻遇的油藏平行,且都位于油层中心。
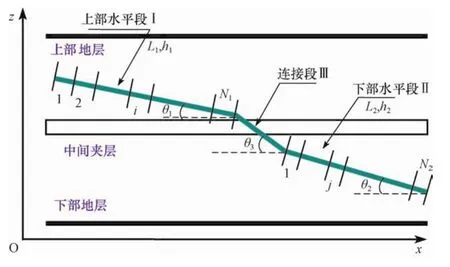
图1 阶梯水平井xoz平面投影及分段示意图Fig.1 Projection and segmentation in xoz plane for stepped horizontal well
将生产段划分为若干微元段:上部水平段Ⅰ等分为N1段,下部水平段Ⅱ等分为N2段,连接段Ⅲ单独一段。设阶梯水平井上部油藏地层倾角为θ1,下部油藏水平井地层倾角为θ2,连接段与水平方向的交角为θ3;上部生产段长度为L1,下部生产段长度为L2,连接段长度为L3;上部油藏厚度为h1,下部油藏厚度为h2,中间夹层厚度为h3。
3 水平井油藏渗流模型
水平井油藏渗流模型可分两种情况:稳定渗流和拟稳定渗流。
稳定渗流模型:采用Joshi[6],Giger[7]等产能公式描述。
拟稳定渗流模型:采用Babu-Odeh公式[8],Helmy-Wattenbarger[9]三维拟稳态流动模型等描述。
当已知油藏和流体的相关参数时,用上述产能方程计算出每段的比产能指数。
4 阶梯水平井沿程压降计算模型
假定水平井筒内为单相不可压缩液体作等温流动。取阶梯水平井上部生产段第i微元段进行分析(图2)。设:各微元段的轴向流量为:qup11,qup12,…,qup1N1;各微元段的单位长度径向流量为:qupr1,qupr2,…,quprN1;各微元段井筒流压为:pupwf1,pupwf2,…,pupwfN1;第i微元段上游端的轴向流量为qup1i1,下游端的轴向流量为qup1i2。
根据质量守恒定理和动量定理得到微元段i井筒压降损失为:
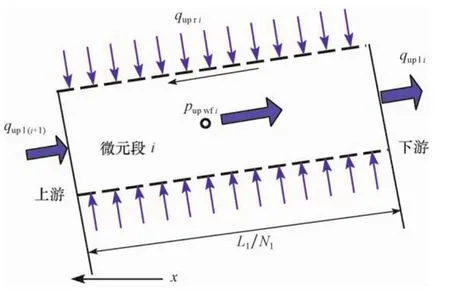
图2 上部水平段第i微元段井筒流体流动示意图[10,11]Fig.2 Diagram showing the flow of fluid in section I of the upper part of the well bore
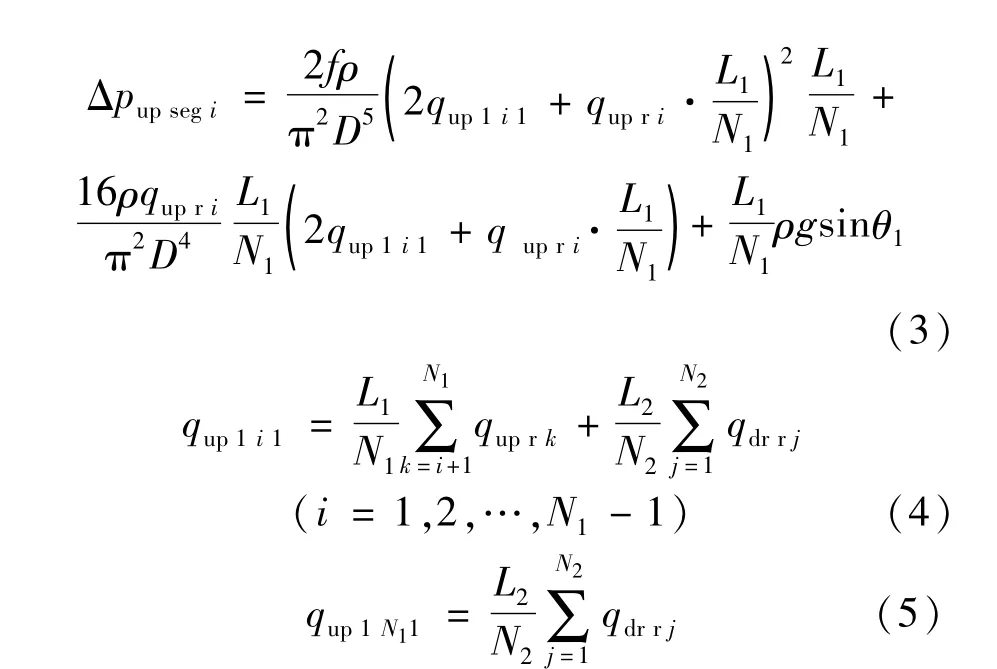
上部水平段第1段下游端的轴向流量即为井筒总流量为:
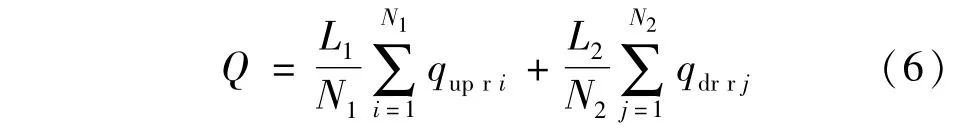
同理,可以得到下部水平段Ⅱ第j微元段井筒压降损失计算模型:
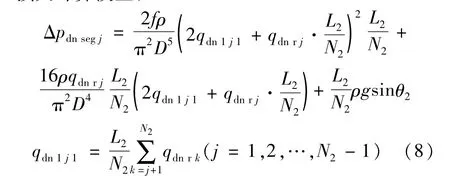
假定下部生产段趾端流量为0,即:
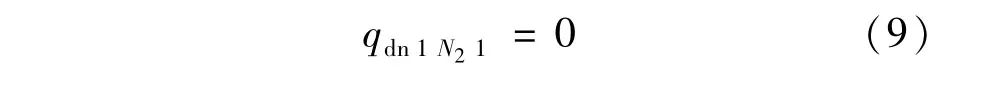
对于连接段Ⅲ仅考虑该段的沿程压降损失,忽略油藏径向流入井筒的流量,可认为连接段内流体的流速大小保持不变,在两端的弯道处只认为改变了流体的流速方向。则该段的压降为:
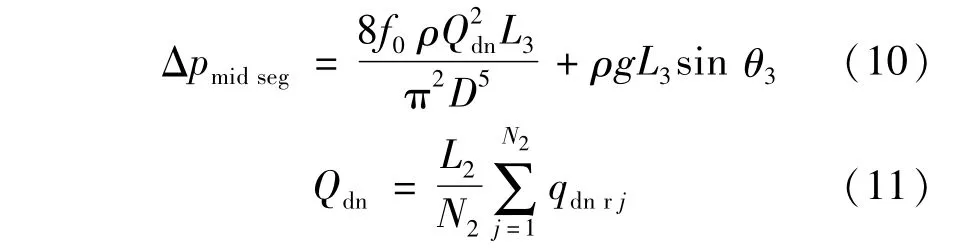
当考虑管壁粗糙度和流体混合产生的摩阻,通过修正摩阻系数f进行校正。
对层流,摩擦系数为:
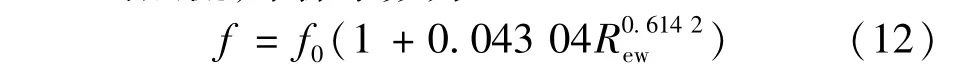
对湍流,根据Liang-Biao Ouyang等的研究结果[7,10],摩擦系数为
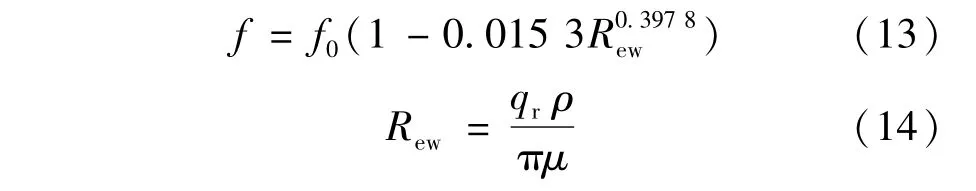
5 阶梯水平井产能预测的耦合模型
将阶梯水平井分成若干小段,由于每一段长度较短,故可假设从油藏流入微元段的流量为均匀分布,但各段流量不相等。设双台阶水平井跟端流压为pwf,则生产段各微元段井筒流压之间的关系为:
上部水平段
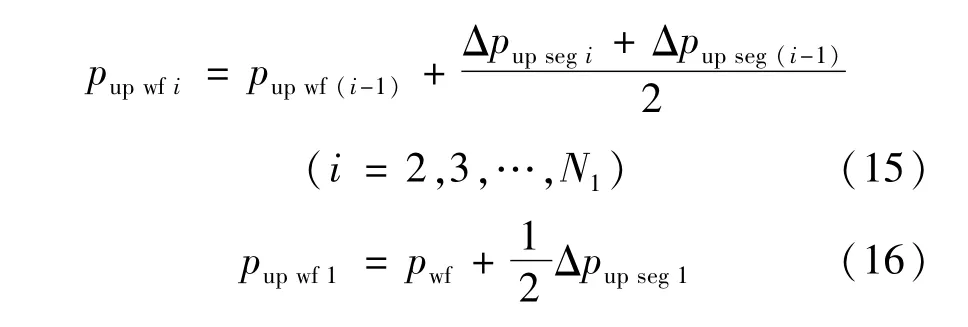
连接段Ⅲ
上端点(与上部生产段的交点)
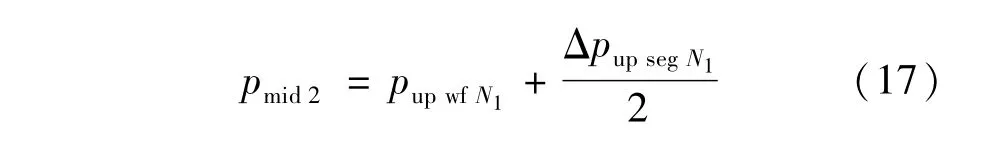
下端点(与下部生产段的交点)
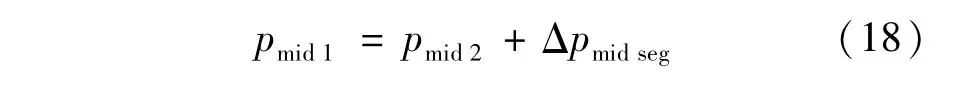
下部水平段
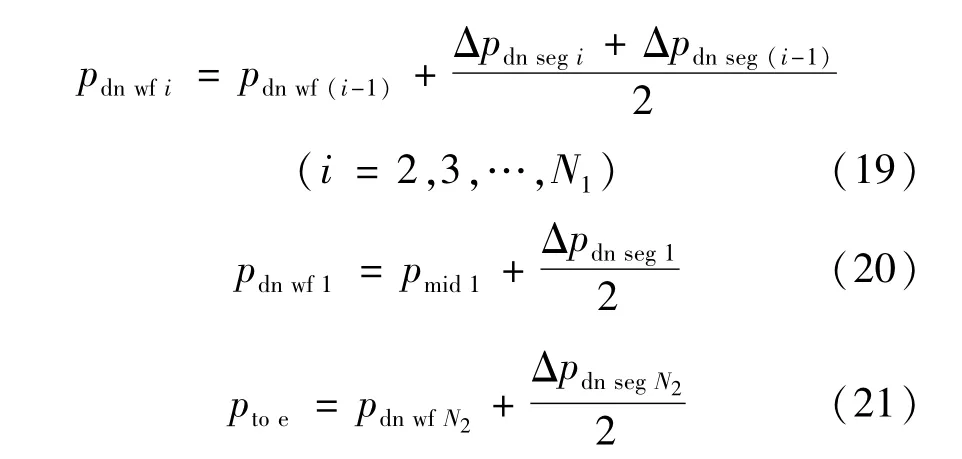
则油藏渗流与井筒耦合的关系为:
上部水平段Ⅰ
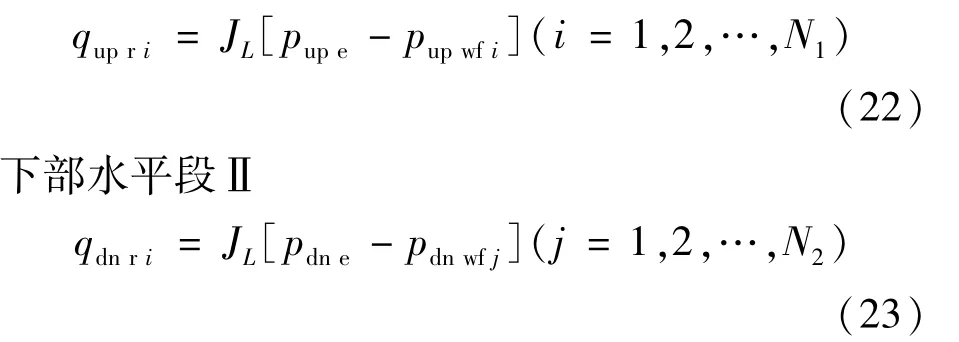
6 阶梯水平井产能计算方法
在上述耦合模型中qupri,qdnri,pupwfi和pdnwfi均为未知数,可采取迭代法求解。先用方程(1)或(2)计算比采油指数,再假设一组pupwfi,pdnwfi值,计算时可假定都等于给定的pwf,用方程(22),(23)解出qupri,qdnri,然后将其代入压降方程(3)—(21)中更新pupwfi,pdnwfi,由此完成一次迭代,如此反复,直到qupri,qdnri,pupwfi和pdnwfi达到一定计算精度为止。最后由式(6)求得全井产量。
7 应用计算
采用文献[11]中提供的一口阶梯水平井的地层参数和钻完井数据对本文建立的模型进行了应用计算,其中比产能指数采用JOSHI公式确定。为了对比分析,采用JOSHI产能公式计算两口分别钻遇薄层油层的水平井产能之和(表1,表2)。从表2中的结果可以看出,因为井筒直径较大,两段水平井筒长度较短,而且井筒截面平均单位长度上流量较小[0.598 4 m3/(d·m-1)不考虑连接段长度],沿程加速度压降可以忽略。主要压降损失产生在连接段,为重力压降损失。在这种情况下,采用JOSHI公式进行简单估算是可行的。
为了说明相关参数对水平井产能的影响,本文计算了其他几种情况(改变上例中的一种参数,其他参数保持不变)(表3)。从表3可以看出,井斜角对双台阶水平井的产能影响较大,也就是说重力引起的压降比摩擦压降和加速度压降都大,占井筒压降的主要部分。因此,设计和钻进双台阶水平井时应使水平段尽量水平,以减少重力压降对产量的影响。
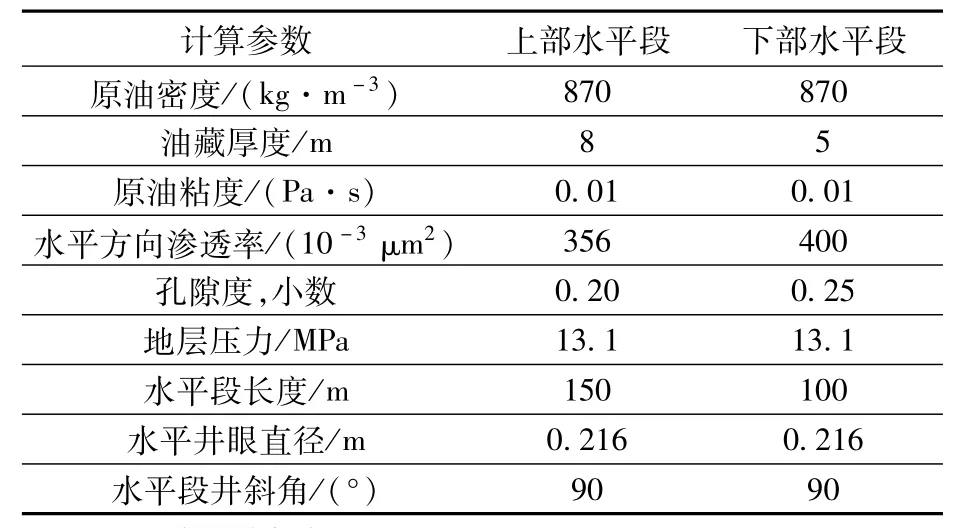
表1 阶梯水平井产能计算参数Table 1 Parameters for calculating productivity of stepped horizontal wells
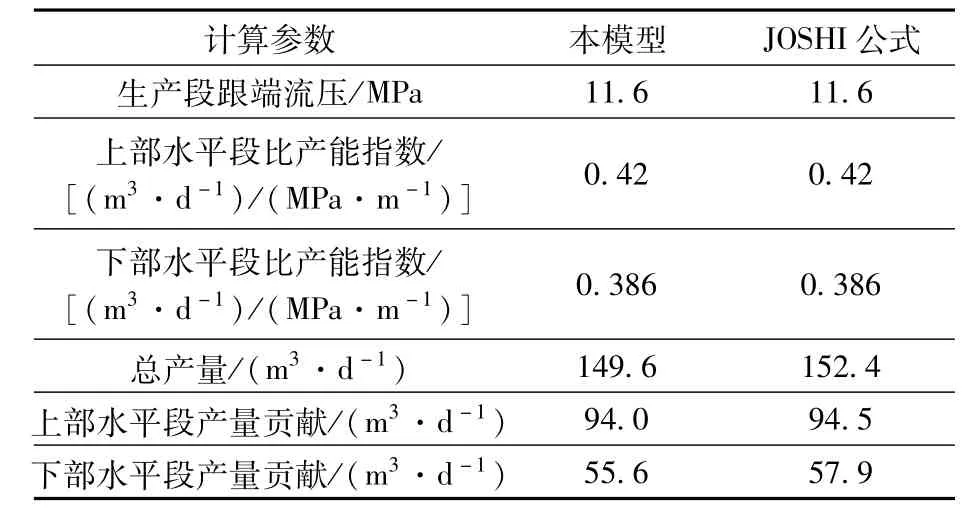
表2 阶梯水平井计算结果Table 2 Calculation results of stepped horizontal wells
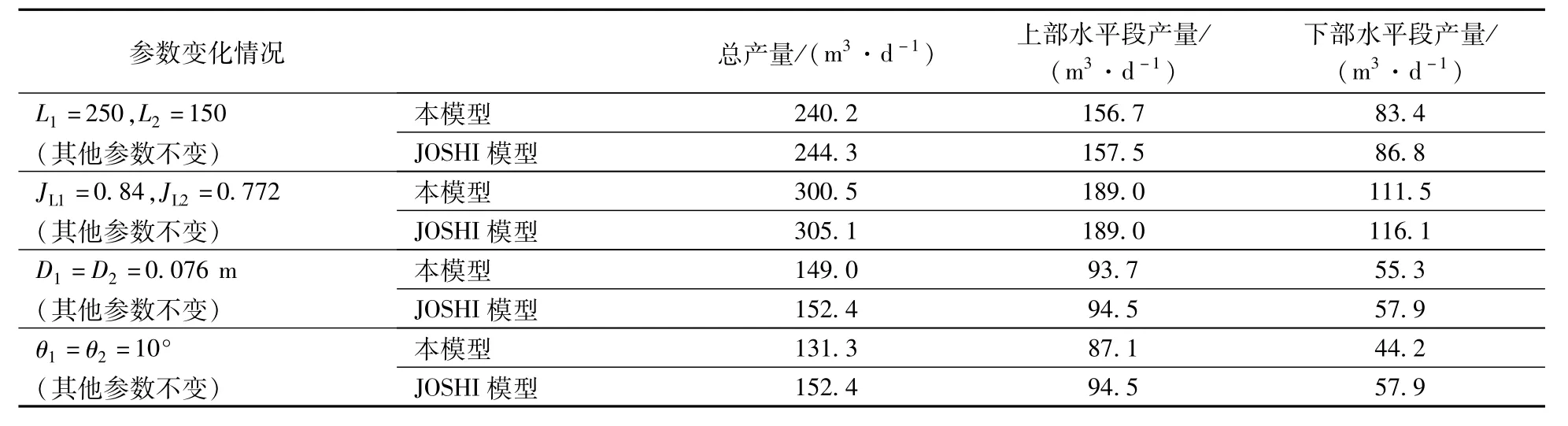
表3 其他参数对水平井产能的影响Table 3 Influences of other parameters on deliverability of horizontalwells
符号注释
D——井筒直径,m;
f0——没有井壁流入时的摩擦系数,无因次;
f——考虑壁面流入时的摩擦系数,无因次;
h1——上部油藏厚度,m;
h2——下部油藏厚度,m;
h3——中间夹层厚度,m;
JL——比产能指数,(m3·d-1)/(MPa·m-1)
L1——上部生产段长度,m;
L2——下部生产段长度,m;
L3——中间连接段长度,m;
pdne——下部油藏地层压力,Pa;
pdnwfj——下部生产段第j微元段的井筒流压,Pa;
pmid1——连接段与下部生产段交点处的井筒流压,Pa;
pmid2——连接段与上部生产段交点处的井筒流压,Pa;
ptoe——双台阶水平井趾端流压,Pa;
pupe——上部油藏地层压力,Pa;
pupwfi——上部生产段第i微元段的井筒流压,Pa;
pwf——双台阶水平井跟端流压,Pa;
qdn1j1——下部生产段第j微元段上游端的轴向流量,m3/s;
qdn1j——下部生产段第j微元段的轴向流量,m3/s;
qdn1N21——下部生产段第N2微元段上游端的轴向流量即趾端流量,m3/s;
qdnrj——下部生产段第j微元段的单位长度径向流量,m3/(s·m);
Qdn——下部生产段总流量,m3/s;
qr——单位长度壁面流入量,m3/(s·m);
qup1i1——上部生产段第i微元段上游端的轴向流量,m3/s;
qup1i2——上部生产段第i微元段下游端的轴向流量,m3/s;
qup1i——上部生产段第i微元段的轴向流量,m3/s;
qup1N11——上部生产段第N1微元段上游端的轴向流量,m3/s;
qupri——上部生产段第i微元段的单位长度径向流量,m3/(s·m);
Q——井筒总流量,m3/s;
Rew——壁面流入雷诺数;
ΔPdnsegj——下部生产段第j微元段井筒内压降损失,Pa;
ΔPmidseg——连接段井筒内压降损失,Pa;
ΔPupsegi——上部生产段第i微元段井筒内压降损失,Pa;
θ1——阶梯水平井上部油藏地层倾角,(。);
θ2——阶梯水平井下部油藏地层倾角,(。);
θ3——连接段与水平方向的交角,(。);
μ——原油粘度,Pa·s;
ρ——原油密度,kg/m3;
公式中下标符号说明:
up——上部生产段;dn——下部生产段;l——轴向;r——径向;mid——中间连接段;i,j,k——微元段序号;1——微元段上游端;2——微元段下游端。
参 考 文 献
1 冯志明.阶梯水平井钻井技术[J].石油钻采工艺,2000,22(5):22~26
2 郭肖,伍勇.启动压力梯度和应力敏感效应对低渗透气藏水平井产能的影响[J].石油与天然气地质,2007,28(4):539~543
3 鹿洪友,陈小宏,黄捍东.水平井负压钻井渗透率剖面计算模型影响[J].石油与天然气地质,2009,30(3):388~392
4 黄世军,程林松,赵凤兰,等,薄互层油藏中阶梯水平井产能评价模型研究[J].西南石油大学学报,2007,29(3):60~65
5 刘想平,张兆顺,刘翔鹗,等.水平井筒内与渗流耦合的流动压降计算模型[J].西南石油学院学报,2000,22(2):36~39
6 Joshi SD.水平井工艺技术[M].北京:石油工业出版社,1991.72
7 高海红,王新民,王志伟.水平井产能公式研究综述[J].新疆石油地质,2005,26(6):723~726
8 Babu D K,Odeh A S.Productivity of a horizontal well[J].SPE 18298,1989
9 陈卫东,Hill A D.多分支井产能预测方法[J].中国海上油气,2006,18(6):394~398
10 陈要辉,阎铁,刘颖,等.裸眼完井分支水平井井筒压力分布理论研究[J].钻采工艺,2004,27(1):1~3
11 黄世军,程林松,赵凤兰,等.阶梯水平井生产段油藏渗流与井筒变质量管流的耦合模型[J].水动力学研究与进展,2005,20(4):464~471
(编辑高岩)
中图分类号:TE243
文献标识码:A
文章编号:0253-9985(2010)04-0499-06
收稿日期:2009-05-22;修改日期:2010-07-10。
第一作者简介:李苗(1982—),博士研究生,油藏工程。
Deliverability prediction for stepped horizontal wells
LiMiao1,2,Li Xiaoping3and Guo Ping3
(1.SINOPEC Petroleum Exploration&Production Research Institute,Beijing 100083,China;2.Graduate School of Southwest Petroleum University,Chengdu,Sichuan 610500,China;3.State Key Laboratory of Oil/Gas Geology and Exploration Engineering of Southwest Petroleum University,Chengdu,Sichuan 610500,China)
Abstract:Based on the principle of themass conservation law and themomentum conservation principle,we established amathematicmodel of drawdown along the horizontalwellbore and coupled the in-flow in thewellborewith seepage flow in the reservoirs by using specific productivity index.Reservoir filtration calculation in themodel is expressed by the steady-state flow model of JOSHI,and calculation of frictional drawdown in wellbore takes into account the impact of the radial inflow.We also wrote program for themathematic model,so as to calculate and analysis the effect of relevant parameters of the well upon its deliverability.The results show that acceleration drawdown is negligible and frictional pressure-drop is insignificant in bigger borehole with lower deliverability,while that gravitational drawdown caused by inclination of wellbores has a bigger impact upon the deliverability.The article provides a simple,easy and effective way for predicting the deliverability of steeped horizontalwells.
Keywords:open hole completion,coupled model,stepped horizontal well,deliverability prediction

