基于神经网络的生活垃圾低位热值计算模型的研究与应用

张瑛华，张友富，王 洪

（1.中国恩菲工程技术有限公司，北京市，100038；2.国家电网公司直流建设分公司，北京市，100052；3.中国电力科学研究院，北京市，100055）

0 引言

近几年，城市垃圾焚烧发电作为环保和新能源项目得到了快速发展。生活垃圾发电具有能源回收利用和减少环境污染的优点，在欧美及东南亚地区都得到很好的应用和发展[1-6]。如荷兰、法国、德国等国垃圾焚烧率2005年之前就接近1/3，瑞士、新加坡、丹麦、瑞典达到了50%左右，日本更超过了70%。而我国的垃圾焚烧发电处于刚开始发展的阶段。我国焚烧处理的城市生活垃圾仅占10%，完工和在建的城市垃圾发电厂约50座，随着我国经济进一步发展和垃圾无害化处理率不断提高，垃圾焚烧发电产业前景广阔。

生活垃圾低位热值的选取对垃圾焚烧发电厂的设计起着关键性作用，直接影响了垃圾焚烧发电厂的设备选型、投资及运营期效益。目前，工程中常采用实验室测定和经验公式两种方法确定垃圾热值。根据CJ/T 3039—95《城市生活垃圾采用和物理分析方法》中规定，实验室测定法一般采用氧弹式热量计测定，工程中通常采用经验公式法。由于垃圾成分复杂，很难准确计算其热值与各成分之间的关系。同时，在不具备采样测定的条件下，工程中经常会采用经验公式法计算垃圾热值。目前，关于垃圾热值计算的经验公式很多，与实验室测定热值差异也不一样。

本文在总结各城市垃圾热值的基础上，建立了基于神经网络的生活垃圾热值计算模型，一定程度上可以有效预测城市生活垃圾的热值大小。

1 低位热值的计算方法

根据工程经验，要保证焚烧炉稳定燃烧并保证850℃以上烟气滞留时间不小于2 s，炉渣热灼减率小于5%，垃圾平均低位热值应达到4 200 kJ/kg以上[7]。

低位热值是焚烧炉选择的重要依据，其计算主要有3种分析方法，即物理成分分析法、元素分析法和近似分析法。运用最广泛的为Khan物理成分模型[2]和Dulong元素分析模型[8]。

Khan物理成分模型为

式中：H1为低位热值，kJ/kg；F为食物类含量；Pa为纸类含量；Pl为塑料类含量；W为水分含量。

Dulong模型为

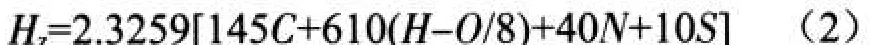
式中：Hz为低位热值，kJ/kg；C为碳含量；H为氢含量；O为氧含量；S为硫含量；N为氮含量。

由于垃圾成分的复杂性，以及成分间的相互作用，使得公式计算结果与实际热值之间有较大的误差。而神经网络能进行联想和记忆推理，因而具有很大的容错性，对于不精确的、矛盾和错误的数据，它都能进行推理并得出很好的结果。神经网络的知识处理系统不存在知识获取的瓶颈问题，具有很强的容错、信息的分布式表示、学习和自组织能力，多层神经网络系统更具有强大的解算能力和处理实际问题的能力[9-10]，因而是热值计算和预测的理想工具。本文以以往各城市生活垃圾物理成分为样本训练，建立基于神经网络的生活垃圾热值计算模型。

2 神经网络模型的选择

神经网络是具有快速信息处理能力、分布式信息存储记忆的能力、很高的自适应和自学习能力、较强的容错能力的一类大规模非线性系统，因此它非常适用于生活垃圾热值计算分析这样的非线性和非确定性领域。

神经网络的知识获取并不需要知识工程师从领域专家的经验中提取，它只是对大量热值试验数据进行学习，自动从试验结果中提取知识，获得的知识隐含地分布储存在神经网络中。

在选择神经网络模型时，采用前向多层神经网络模型，即BP（back propagation）模型，其在训练网络时采用误差逆向传播算法。理论上现已证实，在网络隐含层节点根据需要设定的前提下，3层BP神经网络可以实现以任意精度逼近任意连续函数的功能。因此，采用3层网络的拓扑结构形式，组成输入层、隐含层与输出层3部分，如图1所示。

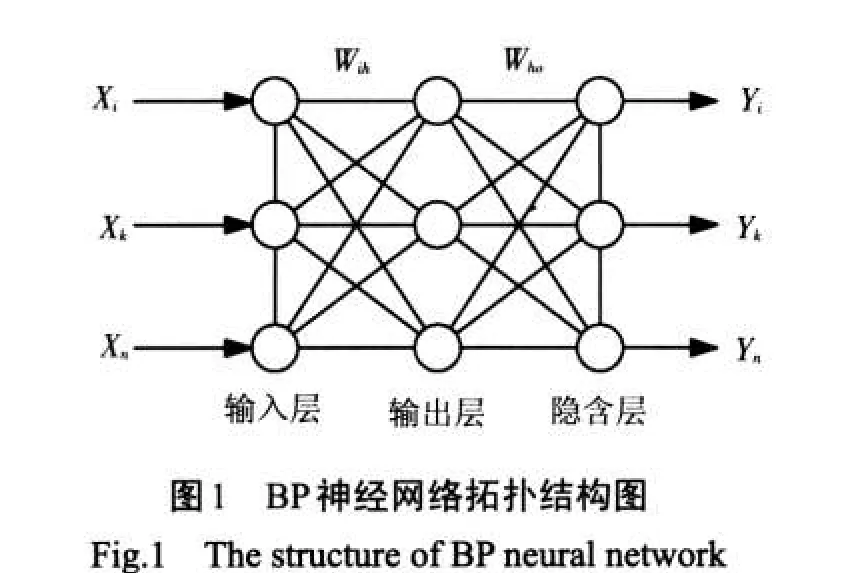
网络知识获取算法的基本思路是：对于给定的输入值[X X]，通过网络特性函数计算输出层的输出值[Y Y]，并与预先的设定值对比，得到误差。然后将输出层节点的误差逐层向输入层逆向传播，分配给各连接节点，从而计算出各连接节点的参考误差，并据此对各个连接节点的连接权[W W]进行相应调整，得到适应要求的网络映射关系，使最终的输出层误差限符合要求的最小值。

3 神经网络分析模型的研究

3.1 神经网络系统的结构设计

隐含层神经元数目采用式（3）确定

式中：Nh为隐含层神经元数；Ni为输入层神经元数；No为输出层神经元数；r为0～10间的整数[9]。

网络特性函数采用Sigmoid函数，见式（4）。

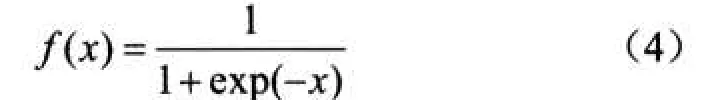
输出层的神经元的实际输出值只能趋近0或1。因此，在设置训练样本时，输入样本及处理输出结果均采用线性比例的导入、导出规则，将输入数据预处理成（0，1）区间的数值，最后将（0，1）区间的输出值转变回原来的表达形式。

3.2 神经网络的训练

神经网络输入参数为9个，分别为各垃圾成分的比例含量：塑料橡胶、纸张、纺织物、木竹、瓜果皮厨余、金属、玻璃、灰土、水分。输出参数1个，为低位热值大小。训练样本选用14个城市生活垃圾的组成百分比和热值大小，如表1[11]所示。BP神经网络系统对14个样本训练情况见图2。当迭代44 651次时，误差小于10-5，表明收敛较好。

4 应用实例分析

训练后的BP网络系统分别对我国3个城市的垃圾热值进行分析。公式法、试验测量法以及BP神经网络法对各工程计算结果如表2所示。

表1 各个城市的生活垃圾组分及热值Tab.Tab.1 1 The solid waste composition and calorific value of various cities

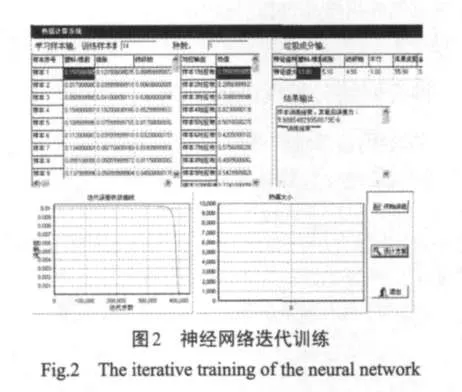
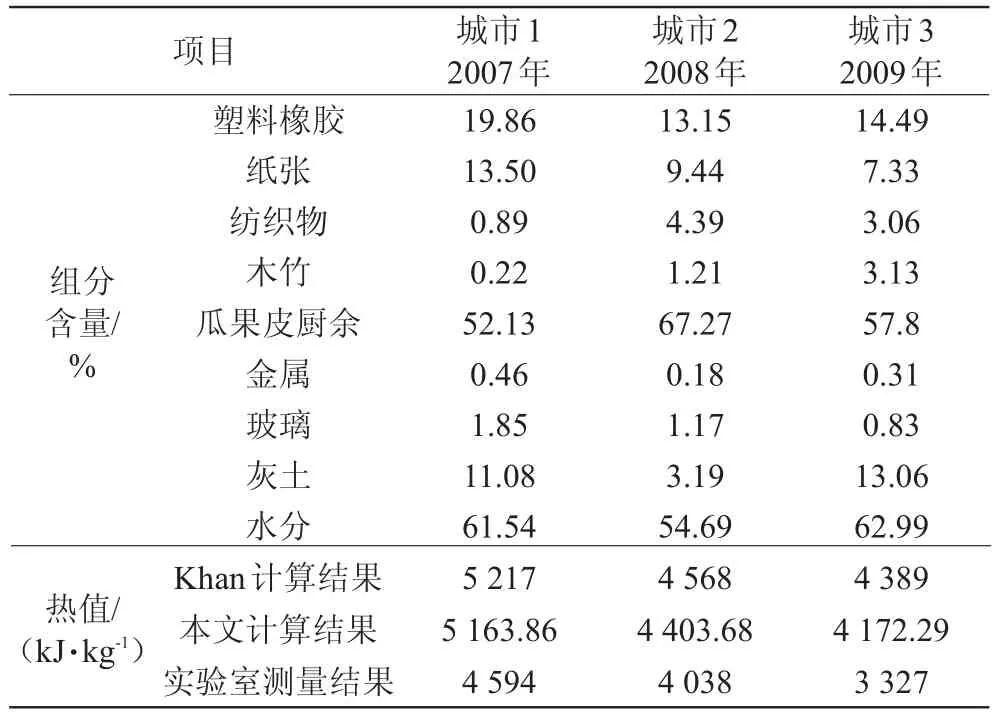
表2 各个城市的生活垃圾组分及热值Tab.2 The solid waste composition and calorific value of various cities

从表2的计算结果对比分析可以看出，本文采用的计算模型比Khan物理成分模型计算结果更接近实验室测量结果，偏差在8.30%～11.03%之间。但城市3垃圾的实验测量结果为3 327 kJ/kg，明显低于公式计算及本文计算结果。考虑到垃圾成分分析单位采用各成分样测定热值后加权平均，由于各成分样取样少，实验室测定结果产生偶然性误差的可能性较大。

另外，进一步分析还可以发现，Khan物理成分模型及神经网络模型的计算结果均高于实际测量值。这里主要原因是Khan物理成分计算模型中的各部分为理想成分，实际垃圾中组分受到灰土及水分的腐蚀和污染等影响，热值有一定降低。而神经网络分析模型中的各物理成分因垃圾采样分析时的人工分类存在差异，并且各组分受到灰土及水分等腐蚀和污染等影响不一，热值不同。因此，在应用神经网络模型进行分析时，要根据训练样本情况对结果进行适当修正。

5 结论

本文利用BP神经网络，结合已有的城市垃圾热值数据，建立了基于神经网络的城市垃圾热值计算模型。该模型对几个城市垃圾焚烧工程项目进行分析，结果表明该系统能准确计算热值的大小，满足工程设计的要求。因此，将神经网络引入垃圾焚烧热值的预测计算，有利于准确计算城市生活垃圾的焚烧热值大小，优化设备选型，为垃圾焚烧发电厂的设计、建设和运营提供依据。

[1]Vollebergh H.Environmental externalities and social optimality in biomass markets:waste-to-energy in the Netherlands and biofuels in France[J].Energy Policy，1997，25（6）：605-621.

[2]Abu-Qudais，Moh'd，Abu-Qdais，et al.Energy content of municipal solid waste in Jordan and its potential utilization[J].Energy Conversion&Management，2000，41：983-991.

[3]Murphy J D，McKeogh E.Technical，economic and environmental analysis of energy production from municipal solid waste[J].Renewable Energy，2004，29（7）：1043-1057.

[4]Sufian M A，Bala B K.Modelling of electrical energy recovery from urban solid waste system:The case of Dhaka city[J].Renewable Energy，2006，31（10）：1573-1580.

[5]袁 克，萧惠平，李晓东.中国城市生活垃圾焚烧处理现状及发展分析[J].能源与环境，2008（5）：43-46.

[6]黄生琪，周菊华.谈城市生活垃圾焚烧发电技术现状及发展[J].应用能源技术，2007（3）：42-45.

[7] 许先壁.垃圾焚烧发电技术概要[J].锅炉技术，1999，30（7）：29-32.

[8]Kathirvale S，Yunus M，Sopian K，et al.Energy potential from municipal solid waste in Malaysia[J].Renewable Energy，2003，29（4）：559-567.

[9]李学桥，马 莉.神经网络工程应用[M].重庆：重庆大学出版社，1996.

[10]戴 葵.神经网络实现技术[M].长沙：国防科技大学出版社，1998.

[11]李晓东，陆胜勇.中国部分城市生活垃圾热值的分析[J].中国环境科学，2001，21（2）：156-160.