水位和覆土厚度变化对过江隧道稳定性影响的数值分析
胡俊强,熊启东,何品祥
(1重庆市建筑科学研究院重庆4000202重庆市渝北区公路工程质监站重庆401120)
水位和覆土厚度变化对过江隧道稳定性影响的数值分析
胡俊强1,熊启东1,何品祥2
(1重庆市建筑科学研究院重庆4000202重庆市渝北区公路工程质监站重庆401120)
对于过江地下隧道,研究重点一般放在对围岩承载能力的研究上。本文对过江隧道围岩稳定性分析是结合现有的工程实例,根据实际勘察数据,通过建立模拟过江隧道开挖的有限元模型,分析过江隧道在不同覆盖层厚度以及不同水位高度下的管片衬砌应力与隧道拱顶位移变化规律,可为过江隧道结构设计提供借鉴。
过江隧道;水位变化;覆土厚度;稳定性
1 国内过江隧道建设概况
当今,随着经济及基本建设的加速发展,城市规模的不断扩大,导致人类有限的生存空间越来越小,尤其是因日益紧张的交通压力引发的各种社会及经济问题越来越突出。目前,各类用途的地下空间正引起人们的极大关注,并已经获得广泛的开发,如地铁、地下停车场、地下街道、地下商场。大城市立体交通的发展,特别是沿江(河)城市更是要建立穿江(河)隧道以缓解桥梁的交通压力。我国上海、广州、南京、武汉等地的交通、建设部门相继将注意力转向了水下过江隧道。
自20世纪70年代开始,我国有很多已建或在建的过江隧道[1]。盾构法施工具有安全高效等诸多优势[2-3],尤其在高水压大断面软土越江隧道和城市建筑密集的地铁隧道施工中优势明显。本文主要针对盾构法过江隧道进行研究。在我国,采用盾构法施工先后建成了上海黄浦江底几条隧道[4]:上海打浦路越江隧道(2.761km)、上海延安东路隧道北线(2.261km)、上海延安东路隧道南线(2.437km)、上海大连路隧道(1.27km)、上海明珠线第二期越江隧道(1.16km)、上海复兴东路越江隧道(1.21km)以及四川金堂清江北河隧道过江输气管道工程(0.4km)、三江口过江隧道(1.992km)、重庆长江主航道第一条江底输气隧道(1.062km)、第二条江底输气隧道(0.96km)、重庆忠县长江隧道(1.66km)、重庆主城区排水过江隧道(0.925km)、上海崇明越江隧道(8.95km)、南京纬七路过江隧道(6.16 km)、武汉长江公路过江隧道、杭州市钱塘江过江隧道;此外,南京已经开建了第二条过江隧道(纬三路过江隧道),广州还计划修建洛溪岛至大学城过江隧道和新造至大学城过江隧道,重庆计划修建的朝天门两江隧道等。为了更好地方便城市之间的交通,我国过江隧道工程会越来越多。
2 有限元模型的建立
对于过江地下隧道,研究重点一般放在对围岩承载能力的研究上。本文对过江隧道围岩稳定性分析是根据实际勘察、施工数据,通过建立模拟隧道开挖的有限元模型,计算分析过江隧道在不同覆盖层厚度以及不同水位高度条件下的衬砌应力与围岩位移变化规律,将过江地下隧道围岩承载能力以及围岩和衬砌的实际应力水平作为隧道围岩安全稳定性的判据。
2.1 过江隧道工程概况及参数选择
模型选取以已建的武汉长江隧道工程为工程背景,取对结构最不利的断面,利用大型有限元软件ANSYS进行数值模拟分析,研究不同的水位和覆土层厚度对过江隧道的衬砌稳定性的影响。
武汉长江隧道工程是万里长江首条跨江公路交通隧道。隧道设计为双孔四车道,盾构隧道段长度为2550m,管片外径11.0m,内径10.0m,厚度0.5m。隧道所处地层砾砂和卵石层为主,盾构到达段最小埋深6.9m;江中段隧道最大埋深21.3 m。隧址区长江段水下地层上部由第四系全新统新近沉积松散粉细砂,中粗砂组成,隧道穿过地层位于中部粉细砂层。具体工程地质情况参见文献[5]。各砂石层材料参数见表1。盾构衬砌管片支护参数见表2。
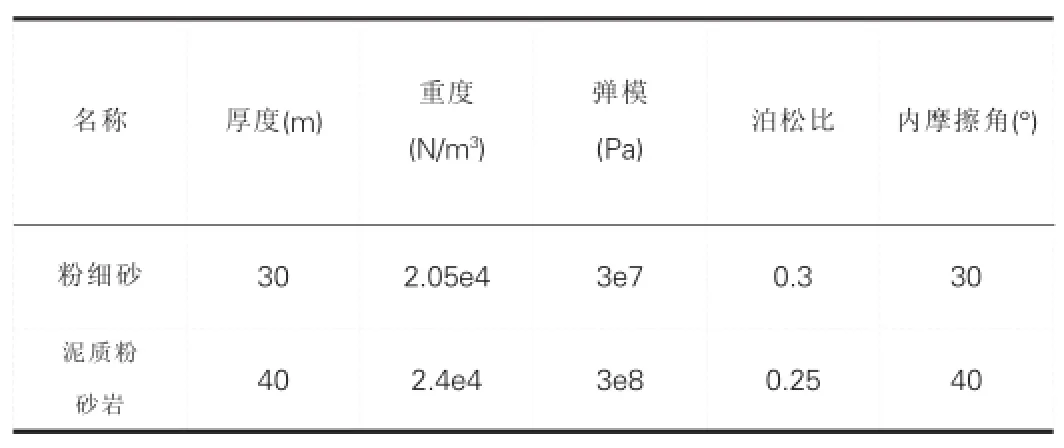
表1 围岩力学参数

表2 衬砌管片材料参数
2.2 过江隧道模型建立
根据武汉长江隧道设计参数,围岩与衬砌管片参数采用表1、表2中参数。隧道围岩模拟采用平面plane42实体单元,衬砌管片采用平面beam3梁单元。计算时围岩使用弹塑性本构关系,屈服准则为DP(Drucke-Prager)准则。隧道左右计算范围取5倍的洞径,下面取4倍的洞径,隧道边界采用法向约束,上边界为自由边界,不做约束处理。
隧道开挖采用盾构机一次开挖,有限元分析过程中通过一次性“杀死”(ekill)需要开挖的岩(土)体单元来实现隧道的全断面开挖。同时激活周边的梁单元来模拟隧道衬砌管片。为了考虑不同水深和覆土厚度条件下的隧道稳定性,本次数值模型分多组情况进行:水深分20m,30m,40m,50m,60m五种,覆土厚度取5m,10m,15m,20m,25m五种。依据不同的水深与覆土厚度分别建模进行计算,最后对计算结果进行对比分析(图1)。
图1 隧道埋深15m时隧道计算模型图
3 计算结果及分析
3.1 围岩内力变化规律研究
过江隧道围应力随着水位高度与覆土厚度的变化而变化,承受的内力主要是压应力,局部会产生拉应力,但数值相对较小。图2、图3所示为5m,10m,15m,20m,25m五种覆土厚度情况下,隧道最大主应力和最小主应力随着水位变化的曲线。
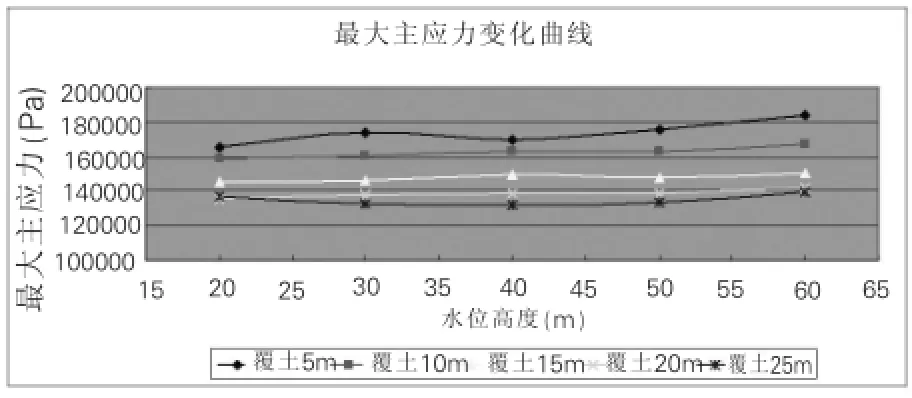
图2 隧道最大主应力变化曲线
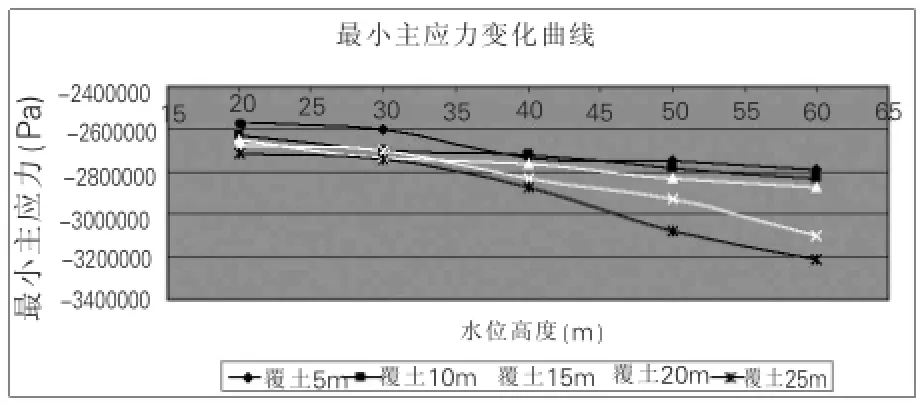
图3 隧道最小主应力变化曲线
由于分析工况较多,限于篇幅,本文仅列出埋深25m、水位高度60m时计算得到的最大、最小主应力云图作为参考,如图4、图5所示。
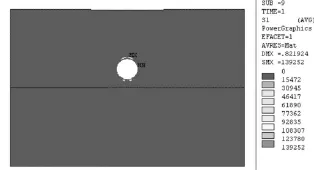
图4 隧道埋深25m、水位高度60m最大主应力云图
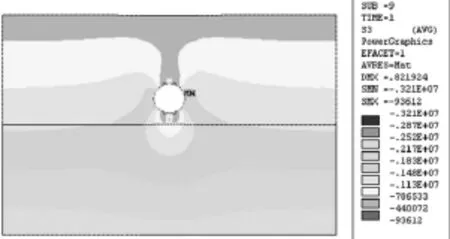
图5 隧道埋深25m、水位高度60m最小主应力云图
经分析对比可知:
(1)同一覆土厚度下,隧道最大主应力和隧道最小主应力(压应力)均随着水位高度的升高有逐渐增大的趋势;同一水位高度下,隧道最大主应力和最小主应力均随着覆土厚度的增加而逐渐增大。
(2)最大主应力的最大值出现在埋深5m、水位高度60m处,其值为0.184Mpa;最小主应力的最大值出现在埋深5m、水位高度20m处,其绝对值最大值出现在埋深25m、水位高度60m处,其值为3.210MPa。
(3)隧道最大主应力为拉应力,最大值出现在圆形隧道的拱顶,拱底处也存在拉应力,但数值较拱顶处偏小,呈左右对称分布,其余部位均未出现拉应力,如图4所示。隧道最小主应力为压应力,其最大值出现在隧道两侧拱腰部位,最小值出现在拱顶和拱底两侧,呈左右对称分布,如图5所示。
3.2 衬砌内力变化规律研究
图6~图8所示为5m、10m、15m、20m、25m五种覆土厚度情况下,衬砌内力随着水位高度变化曲线。
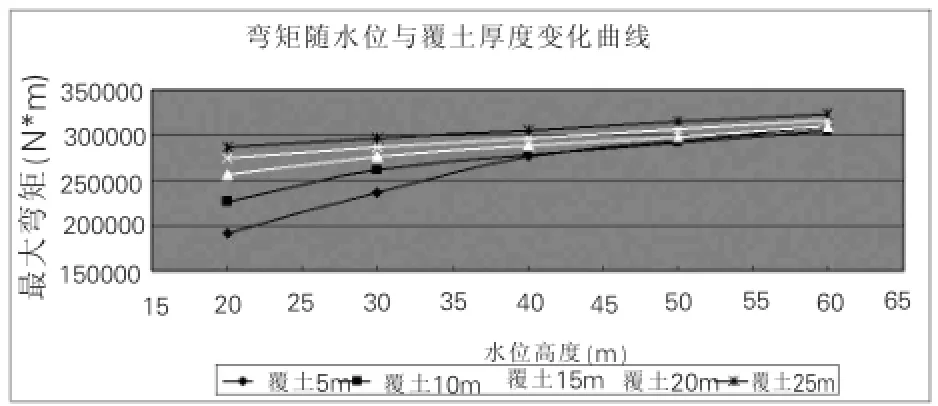
图6 衬砌弯矩变化
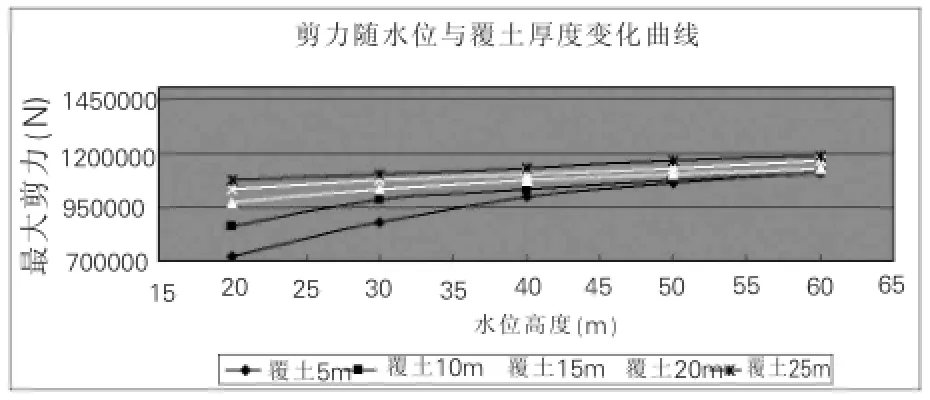
图7 衬砌剪力变化曲线
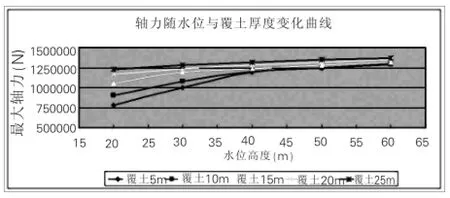
图8 轴力变化曲线
限于篇幅,此仅取埋深25m、水位高度60m时计算得出的衬砌内力图,如图9、图10所示。
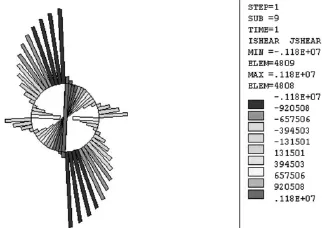
图9 埋深25m、水位高度60m衬砌剪力图

图10 埋深25m、水位高度60m衬砌轴力图
(1)同一覆土厚度条件下,随着水位高度不断增大,衬砌受到的水压力不断加大,管片衬砌结构最大弯矩值、剪力值和轴力均有所增长,弯矩、剪力和轴力值的增幅却随着覆土厚度的增加而变小。如:当水压力从20m变化到60m,埋深5m时的衬砌结构最大弯矩值从191kN·m增大到310kN·m,增幅为62.3%,埋深25m时的衬砌结构最大弯矩值从286kN·m增大到324kN·m,增幅为13.3%,增幅随覆土厚度增大而减小。
(2)同一水位下,衬砌弯矩、剪力和轴力均随着覆土层厚度的增加而增大;弯矩和剪力分布均呈中心对称分布,弯矩、剪力最大值均出现在拱顶与拱底;随着覆土厚度的增加,衬砌轴力随之增大,且增幅较大,轴力基本上呈轴对称分布,最大轴力出现在上拱腰和下拱腰处。
3.3 围岩与衬砌位移与变形规律
图11、图12所示分别为5m,10m,15m,20m,25m四种覆土厚度情况下,隧道X、Y方向最大位移Ux、Uy随着水位高度的变化曲线。

图11 Ux变化曲线图
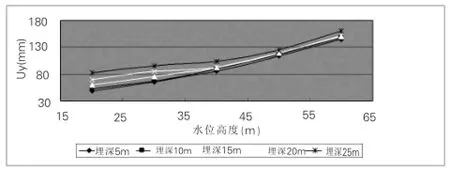
图12 Uy变化曲线图
经过分析对比研究,可以看出:
(1)同一覆土厚度下,隧道X、Y方向的最大位移Ux、Uy均随着水位高度的升高而增大;同一水位高度下,Ux、Uy均随着覆土厚度的增大而增大,但增幅随覆土厚度增加而有所减缓;Ux、Uy的最大值均出现在埋深25m、水位高度60m处,其值分别为0.043m和0.159m。
(2)Ux、Uy均呈左右对称分布,Ux最大值出现在圆形隧道的拱腰部位,呈椭圆形向外依次减小,大约2~3倍直径范围以外的区域Ux=0。Uy最大值出现在拱顶的地表处。隧道影响范围以外的区域(大约2~3倍直径范围)位移均匀层状分布,影响范围以内区域隧道开挖引起洞顶上部下沉,拱底下部反弹,从而产生较大的Y方向位移。
(3)从隧道开挖变形方面来说,当水位高度60m、埋深25m时,隧道变形最大。隧道开挖之后,隧道洞顶对应地表处向下沉降深度最大,向两侧依次减小。与之对应的隧道洞顶处围岩沉降变形最大,极端情况下会有拉裂纹产生,可能由此产生破坏。
4 水位和覆土厚度对过江隧道内力影响理论分析
对于过江隧道,考虑到过江隧道江中部分水位通常很高,江岸部分地下水位通常也不会低于隧道拱顶,故分析时隧道最低水位取为隧道拱顶,即内力计算时采用已有修正惯用法侧向水平荷载为标准梯形形式。水位假定在隧道断面上方,荷载分布于整个管片断面高度范围内,可分解为矩形荷载和满跨三角形荷载进行求解,如图13所示。

图13 修正常用设计法荷载图
其中,P附为附加荷载,Pe、qe为土压力,Pw、qw为水压力,Hw为水位高度。具体公式图形参见文献[7]。
由前文可知:隧道最小埋深6.9m,江中段最大埋深21.3m。理论分析时覆土厚度取实际最小和最大覆土厚度之间的4种工况,分别为6.9m,12.0m,17.0m,21.3m,水位高度从管片拱顶至实际最高水位依次变化,管片弹性模量为36.0GPa,据文献[7]:取刚度折减系数:η=0.8,接头弯矩增大系数:ζ=0.3。据《日本隧道盾构新技术》中已有修正惯用法理论,分别求得内力解析解[6]。
则6.9m,12.0m,17.0m,21.3m,4种覆土厚度下管片最大内力随水位升高的变化趋势分别如图14-图16所示[6]。
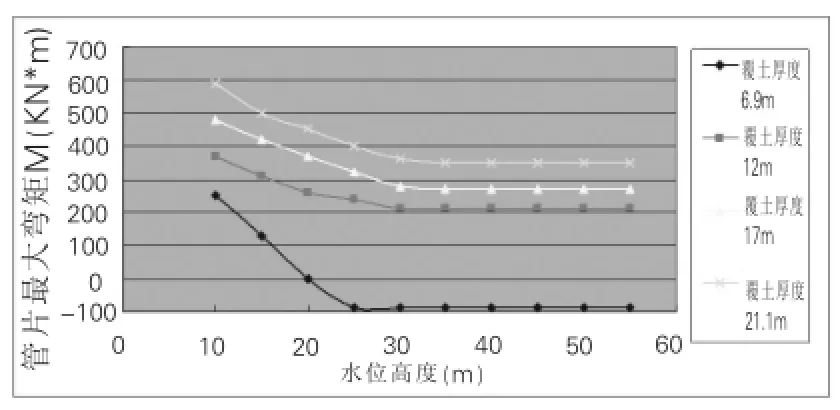
图14 隧道管片最大弯矩变化曲线
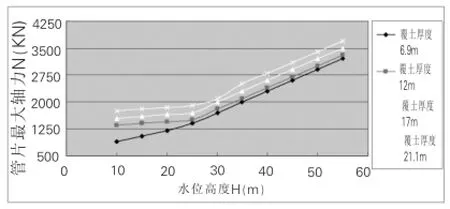
图15 隧道管片最大轴力变化曲线
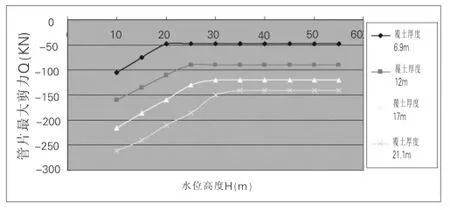
图16 隧道管片最大剪力变化曲线
由图中可以看出:
(1)管片最大轴力随水位上升而增大,呈线性变化的趋势。管片最大弯矩拱顶和拱底处均随水位升高而趋于稳定。通常情况下,拱顶弯矩大于拱底弯矩。管片最大剪力随水位升高而减小(绝对值减小)后趋于稳定而变化不大。
(2)当水位相对较低时,管片最大轴力出现在拱腰,随水位上升,管片最大轴力位置由拱腰向拱底转移,覆土越浅,最大轴力出现在拱底所需的水位越低。
5 结论
本文通过对不同水位和不同覆土厚度条件下盾构隧道的数值模型进行计算分析,得出如下结论:
(1)由以上分析可知,隧道最大压应力出现在两侧拱腰部位,在隧道运营过程中可能会因压应力过大产生破坏,隧道失稳。因此,拱腰部位的衬砌需做特别抗压加强处理。这已在实际工程中得到了验证。
(2)从不同工况计算结果可以看出,Ux、Uy的最大值均出现在埋深最深,水位最高处,其值分别为0.043m和0.159m。由于数值模型考虑上覆土层为粉细砂层,导致竖向变形过大,因此,遇到类似地质条件时,需先要做好防水,止水带,加强衬砌以防止围岩变形过大而造成隧道失稳;而水平位移主要发生在管片腰部,左右向内收敛,变形较小。
(3)衬砌在较大水土压力作用下,在洞顶和洞底处会产生较大拉应力,拱腰产生较大压应力,引起隧道由圆形变为椭圆形。因此,在进行过江隧道规划设计时,仅从围岩变形方面来讲,椭圆形比圆形隧道受力形式更为科学。
(4)通过数值分析与理论分析的对比,可以看出:隧道管片衬砌的最大轴力随水位上升而增大,基本上呈现线性变化的趋势。
(5)由于本文模拟水位情况与文献[6]考虑隧道受力模型情况有所不同,这导致有限元模拟计算得出的内力值整体上略小于理论值;在约25m之前水位变化趋势有所相悖,但剪力和弯矩值变化趋势都是随着水位的变化而最终趋于稳定。
本文仅考虑水位为某一特定值,没有考虑水位随时间的变化的情况,对于其他情况,可以根据本文的计算方法作进一步的探讨。
[1]杨红禹,周建民.论我国过江隧道的发展[J].地下空间,2000,20.
[2]刘建航,侯学渊.盾构法隧道[M].北京:中国铁道出版社,1991.
[3]土木学会.隧道标准规范(盾构篇)及解说[M].朱伟,译.北京:中国建筑工业出版社,2001.
[4]姜天华,刘玲丽.武汉过江新通道探讨[J].武汉交通管理干部学院学报,2002,4.
[5]何川,张建刚,杨征.层状复合地层条件下管片衬砌结构力学特征模型试验研究[J].岩土工程学报,2008,10.
[6]黄清飞,袁大军,王梦恕.水位对盾构隧道管片结构内力影响研究[J].岩土工程学报,2008,8.
[7]尹旅超,朱振宏,李玉珍,等.日本隧道盾构新技术[M].武汉:华中理工大学出版社,1999.
[8]钟祖良,刘新荣,王婷.重庆朝天门两江隧道工程可行性探讨[J].现代隧道技术,2007,06.
责任编辑:余咏梅
Numerical Analysis of Influence of Water Level and Soil Thickness Changes on Stability of Underwater Tunnels
In the aspects of underwater tunnel studies,the research is generally focused on the carrying capacity of the surrounding rock.But in this paper,analysis of the rock stability is performed through a combination of the following elements:the current engineering practice,the establishment of modeling tunnel excavation in finite element model of river-crossing tunnel based on actual survey data;and analysis of arch stress and displacement variation of the segment lining at different heights and different water levels.The writers hope this can provide a reference for the designs of underwater tunnel structures.
underwater tunnel;water level changes;soil thickness;stability
U456
A
1671-9107(2010)11-0006-05
重庆市建设科技项目(城科字2005第(29)号)
10.3969/j.issn.1671-9107.2010.11.006
2010-7-2
胡俊强(1984-),男,工程师,主要从事特种工程施工等方面的设计和施工。

