不同雷诺数下90°弯管内流动特性的数值研究

孙业志, 胡寿根, 赵 军, 仲志刚

(上海理工大学能源与动力工程学院,上海 200093)

流体在弯管内的流动是管道流动的常见现象, 广泛的应用于气体钻井、石油钻探、水利工程、给排水工程、食品加工、煤气和天然气输送工程等工业流程中,特别是90°弯管应用尤其广泛.自1927年圆形截面弯曲管道内存在二次流动首次被提出以来,众多研究者对此格外关注[1-4].T aylor[5]采用激光多谱勒测速仪对90°弯管内发展的层流和湍流进行测量,得到了诸如时均速度、脉动速度分布,以及弯曲段壁面的压力分布等重要物理参量的实验数据.Sudok等[2]采用旋转探针技术对弯管的半径比为2的90°圆形截面弯管内的紊流场进行了实验研究,并给出了若干个轴向截面的速度等值图、矢量图以及雷诺应力等值图等.马材芬等[6]使用激光多普勒测速仪测量了弯管的半径比为1.69,截面为矩形的弯道内正在发展的紊流平均流动和脉动流动,发现在弯道内存在的二次流动比充分发展的紊流条件下要强烈,并且受二次流的影响,湍流存在强烈的各向异性,导致沿程脉动流和平均流之间的能量交换更加强烈.桂绍波等[7]利用基于SMAC方法和交错网格技术,发展了一种在贴体坐标系下求解三维不可压缩流动的数值算法,并应用该方法求解以逆变速度和压力为未知变量的Navier-Stokes方程,对三维90°方形截面弯管内部不可压缩流场进行了数值模拟.江山等[8]对圆管内部流场进行了三维数值模拟,对二次流的产生原因和变化情况进行分析,得出了二次流影响管道内壁压力速度大小的分布规律.本文利用FLUENT软件中RNG k-ε模型,模拟了不同Re下空气在90°圆形截面弯管内的流动.对管内不同部位的压力分布、二次流动以及壁面上压力系数变化等方面进行了分析.此外,针对以往研究较少的低Re时对流场结构及流动特性的影响,本文进行了对比分析,以期为进一步研究流场重要参量在不同Re数下的分布情况奠定基础.

1 数学模型

1.1 控制方程

所用流体介质为常温空气,密度ρ为1.225 kg/ m3,运动黏度μ为1.789 4×10-5kg/(m·s).假设空气以不同的流速连续稳定地流经弯管,大小分别为0.2,1.0和5.0 m/s.由于流速小,可认为是不可压流体.通过对连续方程和瞬时Navier-Stokes方程时均化,得到直角坐标系下绝热、定常、不可压缩流体流动遵循的控制方程.

连续性方程

运动方程

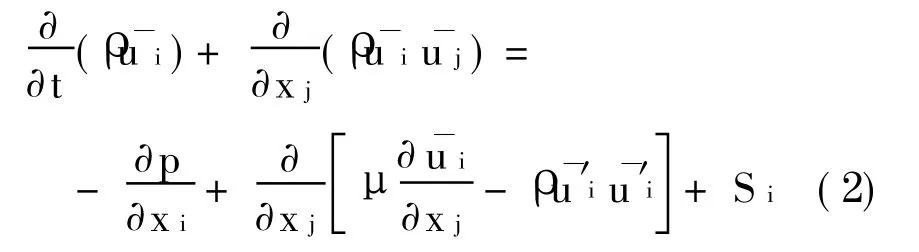
1.2 RNG k-ε湍流模型

RNG k-ε模型由Yakhot和Orzag应用重整化群方法提出,该模型中通过在大尺度运动和修正后的黏度项体现小尺度的影响,而使这些小尺度运动有系统地从控制方程中去除[9].RNG k-ε模型既适应高Re情况,也适应低Re下的湍流流动,即提供了一个微分形式的有效黏性系数表达式,以说明低Re流动效应.

湍动能k

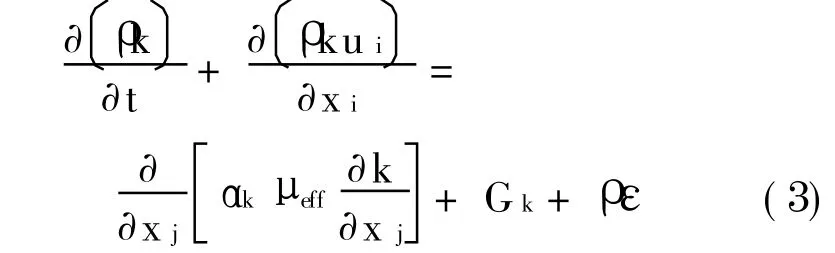
湍动耗散率

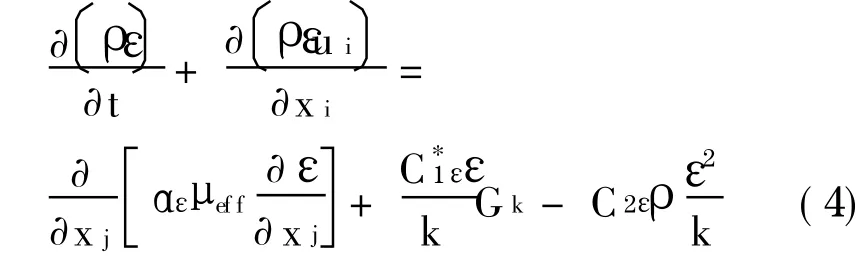
其中

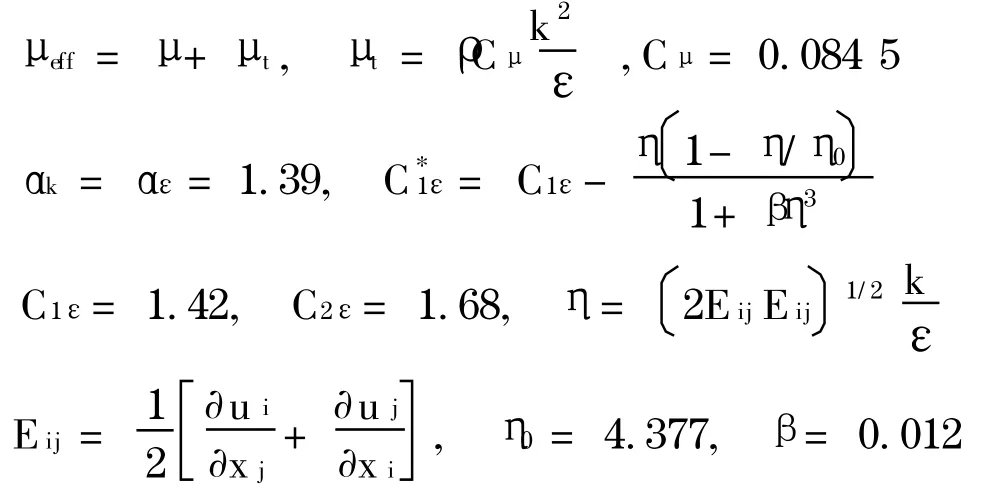
RNG k-ε模型通过修正湍动黏度,考虑了平均流动中的旋转及旋流流动情况;在ε方程中增加了一项,从而反映了主流的时均应变率Eij,这样RNG k-ε模型中产生项不仅与流动情况有关,而且在同一问题中也还是空间坐标的函数.从而, RNG k-ε模型可以更好地处理高应变率及流线弯曲程度较大的流动.文献[10]中对标准k-ε、Rea-l izable k-ε和RNG k-ε模型进行了比较,认为RNG k-ε模型结合两层壁面模型的处理,能更好地数值模拟强曲率影响的弯管内湍流流动问题.

2 计算方法

2.1 模型建立及其网格划分

物理模型为90°弯曲管道,其几何尺寸如图1所示.为便于分析,将管道分成上游直管段、弯曲段和下游直管段3部分.管内径D为0.06 m,弯管的半径比Rc/D为=11.92,上下游的直管段长度均为0.6 m;原点O位于弯管曲率的回转中心;θ为极角,并定义弯曲段的主流入口截面处θ为0°,弯曲段出口截面处θ为90°.

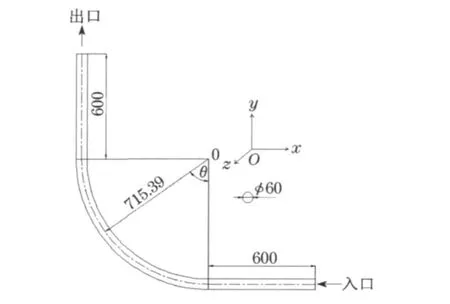
图1 弯管的结构示意图Fig.1 Schematic diagram of bend

利用GAMBIT软件生成计算区域几何体并划分网格,生成的网格为六面体结构网格.

2.2 边界条件

计算中,在入口处采用速度入口边界条件,入口速度为均匀分布,方向垂直于弯管的入口截面即y -z平面;出口采用自由出流条件;壁面上采用无滑移边界条件,采用标准壁面函数法处理.RNG k-ε模型针对充分发展的湍流有效,即适用于高Re的湍流计算模型,只能用于湍流核心区的流动,对壁区内的流动则不适用.解决这一问题有两种方法,即采用壁面函数法或低Re的k-ε模型.壁面函数法因为计算效率高,工程实用性强,对各种壁面流动都非常有效[9],所以采用标准壁面函数法作近壁面处理.

2.3 计算方法及参数设置

数值求解采用SIMPLE算法求解压力-速度耦合问题,时间项采用二阶精度的全隐差分格式,对流项采用QUICK差分格式,扩散项采用中心差分格式.进口空气流速设定为0.2,1.0和5.0 m/s,Re分别为821.5,4 107.5和20 537.6,流动分别为层流、过渡流和湍流.

3 计算结果与分析

3.1 压力分布与二次流图像

3.1.1 管道压力分布

空气由入口流入,经过弯管后从出口处流出.图2所示为进口流速为5 m/s时(Re=20 537.6,湍流),管道对称中心面(z=0)上压力分布图.在直管段到弯管的进口(θ= 0°)处,截面上压力均匀分布,如图3所示,等压线呈同心圆状.从图2中可以清晰看到,在弯管内,沿径向的压力梯度很大,呈现出靠近内壁面区域的压力值小,而外壁面附近区域压力值较大的分布情况.产生这一现象的主要原因是流体在流动过程中受到弯管曲率的影响,因离心作用向曲率半径较大的外壁面附近移动,导致众多流体推挤外侧壁面所致.流体的压力分布在流出弯管后重新达到均匀.此外,弯管下游直管段处的压力值小于上游直管段处的压力值,这主要是由于分子黏性导致流体沿管道壁面产生沿程损失和二次流损失所引起的.在过渡流(u=1 m/s)和层流(u=0.2 m/s)情况下压力分布情况相似,这里不再赘述.

图2 管道中心截面压力分布Fig.2 Pressure distribution of pipe center section

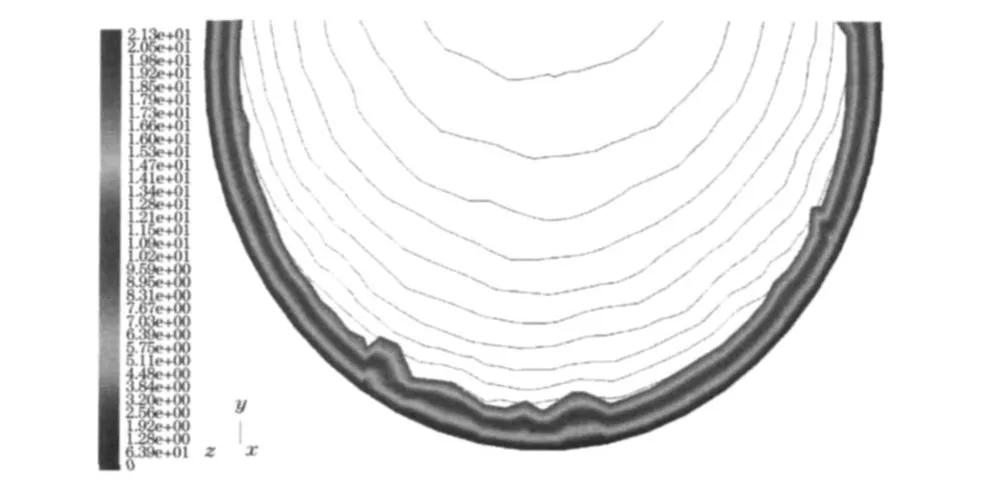
图3 θ=0°截面压力分布Fig.3 Pressure distribution of θ=0°section

3.1.2 二次流图像

流体在大曲率的弯管中运动,由于受到黏性和流场逆压梯度的影响,横截面上会产生二次旋流.二次流导致了弯管内横截面方向上的动能和能量交换,既改变了主流方向的平均速度,又减少了流场的总压.横截面上二次流速度矢量图在Re不同时相似,以Re=20 537.6为例进行说明,见图4.图中上部为外壁面位置,下部为内壁面位置.

从图4中可以清楚地看到二次流的形成与发展过程:在θ=0°的进口截面,气流径向速度都指向内壁,这是由于此处有较大的径向压力梯度所致.进入弯曲段后,流场由于流体惯性和分子黏性的相互作用,各个截面上出现关于z=0对称的二次流涡对.在θ=30°截面可清晰地看到一对二次流旋涡,这种二次流旋涡卷吸附面层内的低能流体并随主流向下游不断发展,在θ=60°截面处达到最大,之后二次流强度有所减弱.由于不可压缩流体的流动具有强椭圆型特征,所以直至弯管出口直管段,弯管曲率对流场的影响仍然十分强烈,二次流依然清晰可见,这与文献[11]的观测结果一致.

图4 弯管段不同截面二次流图像Fig.4 Secondary flow images of different crosssection in pipe segments

3.1.3 弯管段壁面上压力分布

图5所示分别为层流(Re=821.5)、过渡流(Re=4 107.5)和湍流(Re=20 537.6)状态下弯管的中心对称面(z=0)内外两侧壁面上压力分布曲线图.从图中可发现,随着Re的增大,空气对管壁的压力p越来越大.Re越大,管壁压力开始衰减的位置在延后,对于外壁面格外突出.在Re=20 537.6时外壁面上压力几乎不再衰减.分析其原因在于随Re增大,流体湍流脉动在增大,加上二次流的影响使弯管内横截面方向上的动能和能量交换增大,改变了主流方向的平均速度,导致外壁面压力分布趋于稳定.

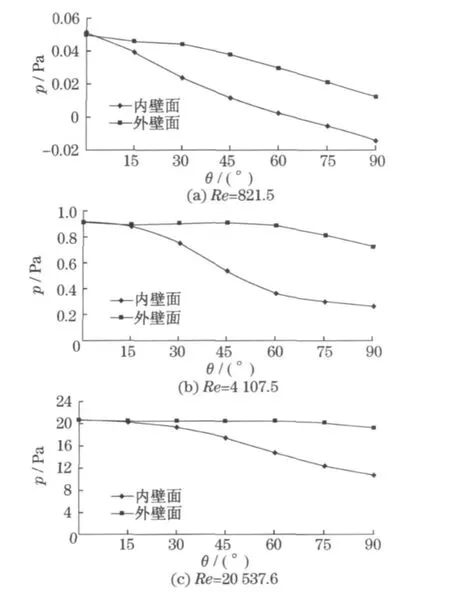
图5 弯管壁面上压力曲线Fig.5 Pressure curve of bend surface

3.2 Re不同时壁面压力系数分布

图6给出了不同Re下展向z=0的对称面上内壁和外壁上压力系数沿弯管中心线的分布情况.定义压力系数Cp=(p-pref)/(1/2ρ u2),其中p为监测点压力,u为进口流速.参考压力pref定义为弯曲段进口θ=0°截面中心点处的压力值.

由图6可看出,弯管及之后的竖直管段内Cp都为负值,说明管内压力小于入口处压力.Re不同时,管道壁面压力系数Cp的大小差别不大.Re越大,管道内同一位置处压力系数的绝对值越小,外侧壁面变化尤其明显.分析其原因,虽然流体受到曲率影响产生的惯性应力在增大,但更主要是随Re增大,流体的湍流脉动增强,湍动能交换强烈,使得流场出现强烈的各向异性.

层流时,在弯管段内外侧壁面上压力系数变化趋势一致,且曲率的影响在之后的竖直管段内5倍管径处已经很小.而湍流时,压力系数沿程变化在弯管段特别明显,随角度的增大在迅速增大且内壁面压力系数变化明显强烈于外壁面处,曲率的影响一直持续到10倍管径处仍很强烈.这主要是由于流体介质沿弯管流动时所受惯性离心力作用所致.此外,由于流场发生分离现象,加上流动过程中附面层变化引起的损失,使得湍流时弯管段管道内外侧壁面上的压力系数变化出现明显不同.

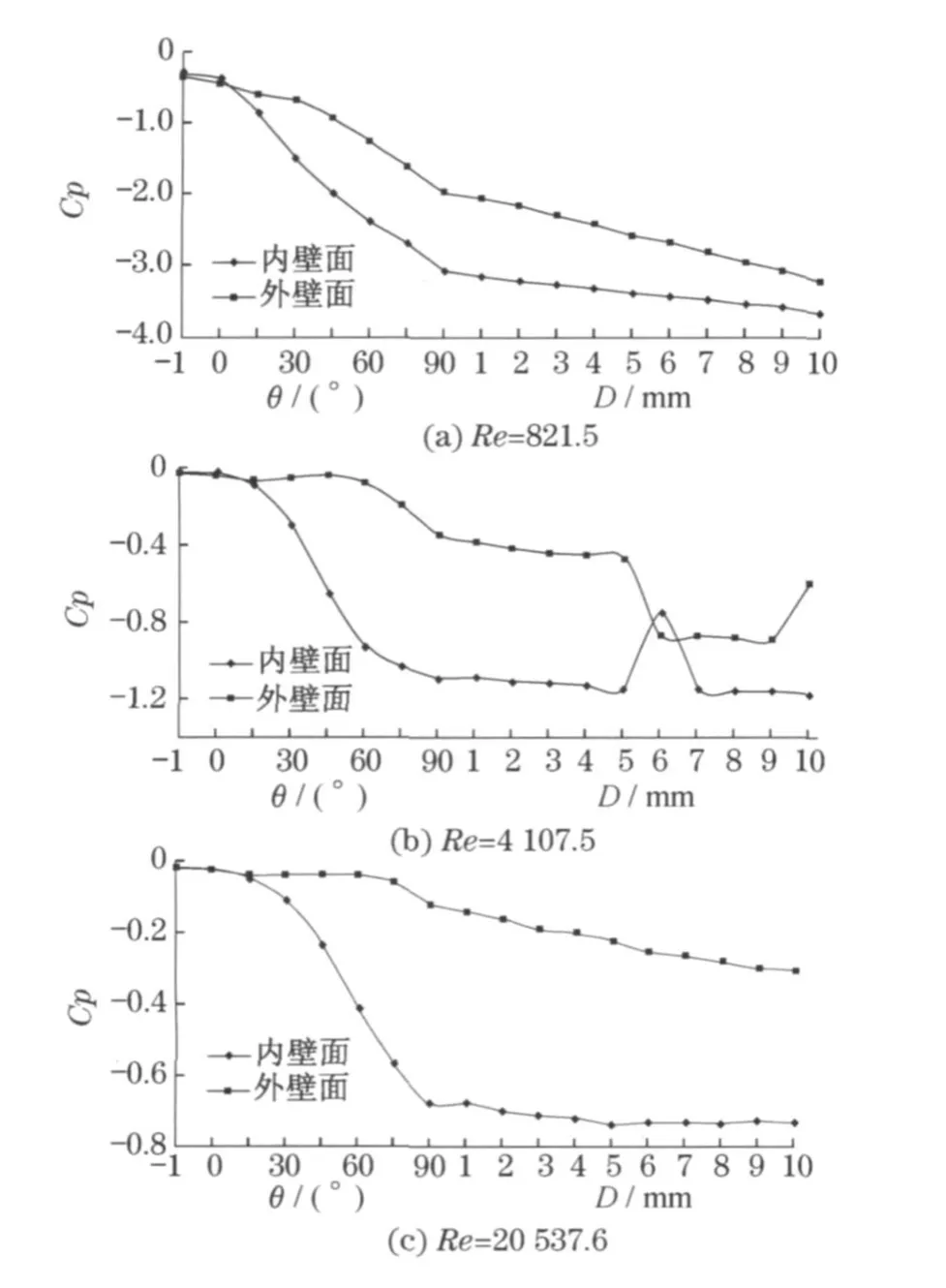
图6 弯管壁面上压力系数分布曲线Fig.6 Pressure coefficient distribution curve on the wall

4 结 论

a.在弯管前后直管段内压力均匀分布;弯管段内空气沿径向的压力梯度很大,呈现出靠近内壁面区域的压力值小,而外壁面附近区域压力值较大的分布情况.

b.在气流进入弯管段后,流场由于流体惯性和分子黏性的相互作用,各个截面上出现对称的二次流涡对.二次流导致了弯管内横截面方向上的动能和能量交换,既改变了主流方向的平均速度,又减少了流场的总压.

c.随Re增大,流体对管道壁面的压力增大,管内压力损失也在增大.原因是流体受到曲率影响产生了惯性应力,流体向外侧堆积导致此处压力增大,随着流体湍流脉动的增大,加上二次流的影响导致了弯管内横截面方向上的动能和能量交换增大.

d.管道壁面上的压力系数随Re的不同差别不大,由于有压力损失,管内Cp均为负值.Re越大, Cp越小,并且外壁面变化比内壁面更加明显.原因在于随Re增大,流体的湍流脉动增强,湍动能交换强烈,使得流场出现强烈的各向异性,使得管内压力分布趋于平均.

e.在层流和湍流时压力系数的变化有很大的不同,湍流时压力系数沿程变化比层流明显很多,曲率的影响也要强于层流.这主要是由于流体介质沿弯管流动时受到惯性离心力作用以及流场发生分离现象导致附面层变化引起的损失,使得湍流时壁面上的压力系数变化与层流明显不同.

[1] DEAN W R.Note on the motion of fluid in a curved pipe[J].Phil Mag,1927,4(2):223-238.

[2] SUDO K,SUMIDA M,HIBARA H.Experimental inves-tigation on turbulent flow in a circular-sectioned 90-degree bend[J].Experiments in Fluids,1998(25): 42-49.

[3] AZZOLA J.Developing turbulent flow in a U-bend of circular cross-section[J].Measurement and Computation Trans ASME,J of Fluids Eng,1986,108:214-221.

[4] 吴望一,谭文长,李娟,等.弯曲圆管内旋涡结构分叉现象的理论研究[J].应用数学和力学,2000,21(12): 1215-1226.

[5] TAYLOR A M K P,WHITELAW J H,YIANNESKIS M.Curved ducts with strong secondary motion:velocity measurements of developing laminar and turbulent flow[J].Journal of Fluids Engineering,1982(104):350-359.

[6] 马材芬,史峰,徐忠.90°弯道内紊流的试验研究[J].工程热物理学报,1990,2(11):37-39.

[7] 桂绍波,曹树良.基于SMAC方法的90°弯管内部流场数值模拟[J].江苏大学学报,2008,29(6):507-511.

[8] 江山,张京伟,吴崇健,等.基于FLUENT的90°圆形弯管内部流场分析[J].中国舰船研究,2008,3(1): 37-41.

[9] 王福军.计算流体动力学分析[M].北京:清华大学出版社,2004.

[10] 丁珏,翁培奋.三种湍流模式数值模拟直角弯管内三维分离流动的比较[J].计算物理,2003,20(5): 386-390.

[11] 樊洪明,张达明,赵耀华,等.90°弯曲圆管内流动数值模拟[J].北京工业大学学报,2007,33(2):174-177.