一种城市公交车发车频率的优化模型

刘安业,徐兆宇,陈 闯

(黑龙江省收费公路管理局)

1 问题分析

行车时刻表的制定是城市公共交通企业管理的重要基础工作之一。如何经济、合理地使用车辆,解决运量和运能的矛盾,挖掘车辆潜力,缓解客流拥挤,是制定行车计划的目标。

1.1 乘客需求分析

乘客乘坐公交车最为关注的是车内拥挤度及等车时间,而车内拥挤度、等车时间主要和公交调度相关,可以从安排车辆运营角度考虑乘客需求,减少拥挤和等待,这就要求车辆足够多。但无论从企业运作、经济效益考虑,还是考虑道路条件限制,都不可能达到理想要求。因此,行车计划只能在一定程度上满足乘客需求。

1.2 公交企业效益需求分析

公共交通是劳动密集型行业,决定了企业运作的成本是非常高的。企业每年要承担车辆的投入、维修、保养、人员工资、企业管理费用等一系列费用,而主要收益只来自乘客的票款收入。公交是一种面向工薪阶层的大众交通方式,其票价是按低标准确定的。要提高企业的效益,只能通过降低成本,主要是减少车辆、人员的投入,但又是以牺牲一定的乘客利益为代价的。

综上所述,乘客需求和公交企业需求是一对矛盾,满足乘客需求会牺牲企业利益,以企业利益为重又会损失乘客利益。因此,找到二者的平衡点,制定相应的行车计划,是调度优化的关键。

2 发车频率优化模型

2.1 模型假设

(1)考虑单行方向。

(2)公交车在线路上匀速行驶,不存在堵车现象,准点到达各个站点。

(3)我们把一天(24h)平均分成若干个时段,不失一般性,以 1h为一个时段,且任意一个时段内发车间隔相等。

(4)公交车经过各站会将候车乘客全部带走,无乘客滞留现象。

(5)各站客流在时段内服从均匀分布。

(6)车辆满载率不超过 120%,乘客的等车时间在早晚高峰期不超过5min,在平峰期不超过10min。

(7)全程票价统一。

2.2 模型的变量定义

对模型中涉及到的变量作如下的说明:

l为将全线客流划分为 l个时段;r为线路上的站点数量;xij为在第i时段第j个站点等待上车的人数;yij为在第i时段第j个站点等待下车的人数;mp为公交车额定载客量; hr为乘客能够接受的公交车最大满载率;li为 i时段的时段配车数,则 60/li为i时段的发车时间间隔。

2.3 模型的建立

(1)各时段最大客流断面通过量的确定。

由变量定义知,在第 i时段第j个站点等待上车的人数为xij,在第i时段第j个站点等待下车的人数为yij,则在第i时段内,在站k至k+1之间的断面客流通过量为(xijyij),如果 k取遍 1～r内的所有自然数,就可以计算得到各个站点之间在i时段内的断面客流通过量,则在 i时段内各个站点间的最大客流断面通过量可以表示为

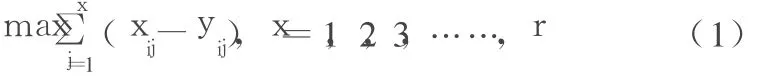
(2)调度模型的约束条件。

①乘客无滞留约束条件。为了保证公交车能够将各个站台的乘客全部带走,则必须保证公交车的车内最大载客量大于等于各时段的最大客流断面通过量。由变量定义知,i时段内的发车时间间隔为 60/li,依据各时段内客流均匀分布的假设,可以推出时段内各发车间隔内最大客流断面通过量为

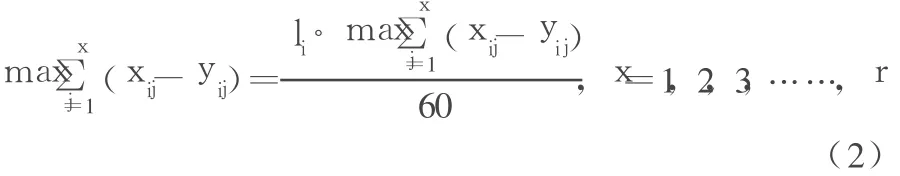
要保证各站无乘客滞留现象,就要保证各发车间隔内最大客流断面通过量小于等于公交车的最大载客量,用数学公式可表示为

②乘客最大等车时间约束条件。由于公交车在全程是匀速行驶的,因此可以近似的认为,公交车在各个时段的发车间隔即为乘客在各个时段的最大等车时间,为满足乘客在早晚高峰期等车时间小于等于 5min,平峰期等车时间小于等于10min的要求,则要保证

(3)模型的目标函数。

拟设计的公交调度模型兼顾公交公司和乘客的双方利益,上述约束条件都是考虑到满足乘客的利益,因此模型的目标函数应该考虑到公交公司的利益。公交公司希望看到发出的每辆公交车都有较大的满载率,以后获得较为丰厚的运营收益,因此可以将公交公司发出的每趟车的载客量最大作为模型的目标函数,即

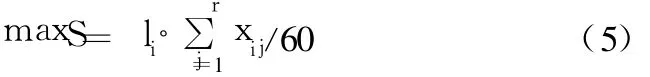
综上所述,公交车发车频率的优化问题可以用(6)所示的数学模型加以表述

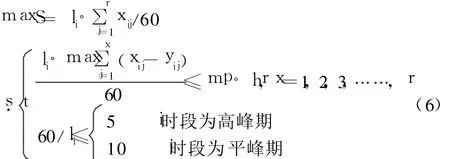
上述模型是一个典型的非线性优化问题。寻优的初值取实际调度的经验值,这样保证在初值附近的一个邻域内,总能找到一个使得)≥S(li),该局部最优解完全可以作为实际问题的近似最优解。借助Matlab数学工具,通过最优化搜索很容易求得。

3 结 论

描述的模型同时兼顾了企业和乘客的双方利益,充分考虑了线路运行的可能性,对客流的处理采用了分时段的思想,使得模型简单便于操作。模型考虑到客流的方向性差异,利于车辆资源充分利用,也便于区域调度安排组织。充分考虑到客流数据的可获得性,使模型在调度的任何发展阶段都具有一定的通用性。

[1] 北方交通大学.城市公共交通运营调度管理[M].北京:中国铁道出版社,2001.

[2] 王炜,杨新苗,陈学武.城市公共交通系统规划方法与管理技术[M].北京:科学出版社,2002.

[3] 戴明强,李卫军,李新鹏.一类公交车调度问题的数学模型及其解法[J].运筹与管理,2004,13(1).

[4] 陈茜,牛学勤,陈学武,等.公交线路发车频率优化模型[J].公路交通科技,2004,21(2).