高职数学建模竞赛教学探析

蔡建刚



高职数学建模竞赛教学探析

蔡建刚

（漳州职业技术学院 基础教学部，福建 漳州 363000）

对高职数学建模竞赛的背景、现状、意义和解题思路进行了探讨和分析，认为高职学生参加数学建模竞赛必须着重进行选拔和培训。

高职；数学建模竞赛；解题思路；培训

1 高职数学建模的背景

数学模型（Mathematical Model）是用数学符号对一些实际问题或实际发生的现象的（近似的）描述，而数学建模（Mathematical Modeling）则是获得该模型、求解该模型并得到结论以及论证是否正确的全过程[1]。大学生数学建模竞赛（The Mathematical Competition in Modeling，简称为MCM）最早是1985年在美国出现的，创始人为Ben A.Fusaro，其参照了普特南数学竞赛，普特南数学竞赛出现于1938年，但它只是作为针对数学系学生的纯数学的学科竞赛而无法得到广泛推广。1989年在几位从事数学建模教育的教师的组织和推动下，我国几所大学的学生开始参加美国的竞赛，经过两三年的参与，认为这种竞赛有利于学生的全面发展，也是推动数学建模教学在高校迅速发展的好形式。于是在1992年由中国工业与应用数学学会组织举办了我国10城市的大学生数学建模联赛。从此，全国大学生数学建模竞赛在我国得到迅猛健康发展，成为国家教育部组织的全国大学生四项学科竞赛之一，专科组于1999年开始参赛。

2 高职数学建模的现状

数学建模竞赛从1992年在全国进行推广以来得到了广大师生的认可并得到迅猛的发展，其规模也日趋扩大。图1列举出了从1992年到2008年以来全国大学生数学建模竞赛参赛的队伍数目。

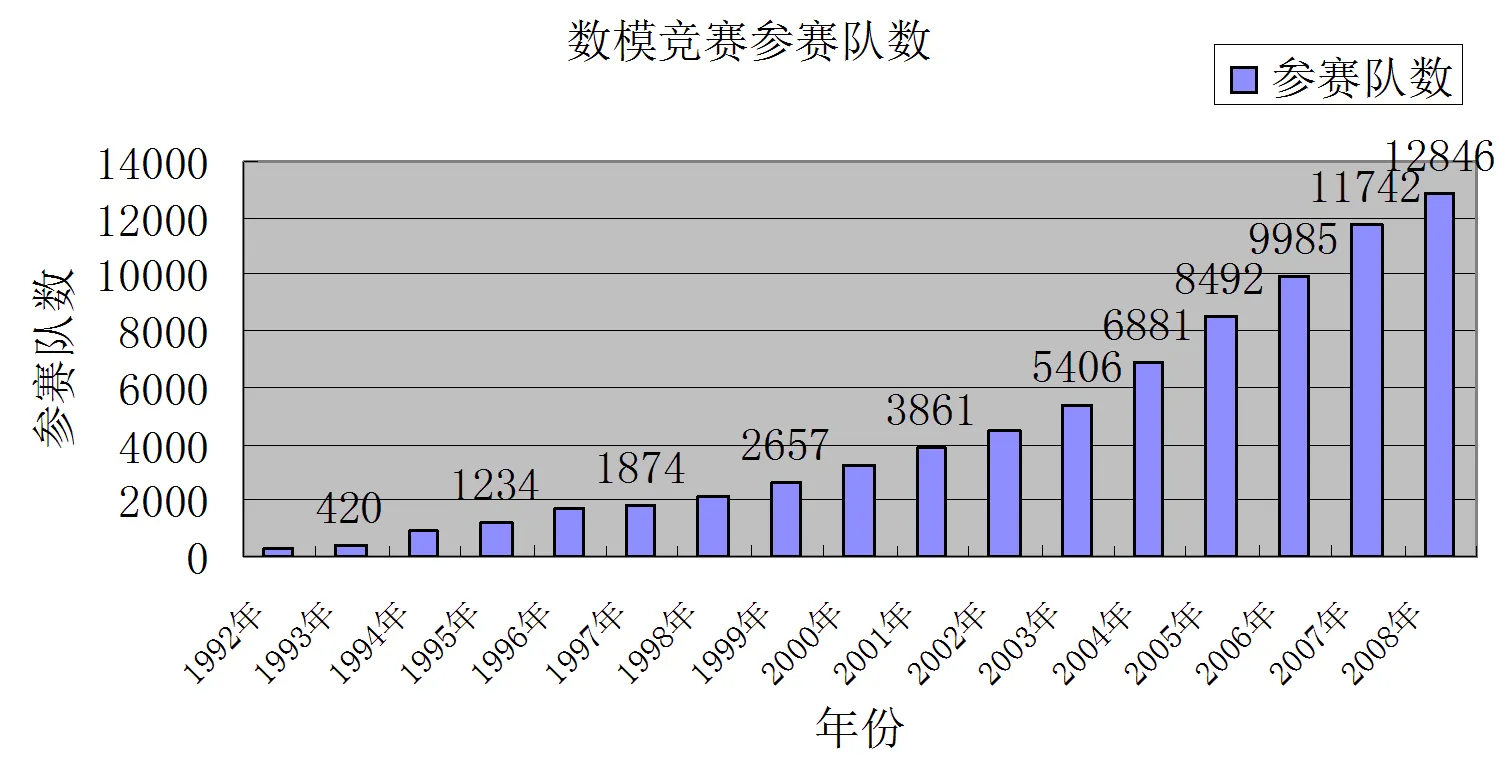
图1 历年数学建模竞赛参赛队数

专科组从1999年开始参赛以来也得到了迅猛发展，从开始的仅本科院校的专科层次学生参赛到现在的越来越多的专科院校参与，高职数学建模体现了其强大的生存和发展能力，但相比较本科组而言还存在着非常大的差距，图2为2000年至2008年以来全国大学生数学建模竞赛本科组与专科组获奖的情况比较。而福建省大学生数学建模竞赛本专科组获奖情况差距相对更大，如图3所示。

图2 历年数学建模竞赛本专科获奖情况表

图3 近年福建数学建模竞赛本专科获奖情况表

3 高职数学建模的意义

数学建模竞赛使高职学生和教师都受益匪浅。

首先教师在认识上得到了升华，明确了数学的教学和教改的途径和方向，充分认识到数学建模是联系实际问题与数学的桥梁，是发现问题、解决问题和探索新真理的工具，是数学知识与应用能力共同提高的最佳吻合点，是培养高素质创新人才的一条有效途径[2]，对于体现数学的应用价值、发挥数学的社会化功能，提高公民的数学素质具有极为重要的意义；其次在教学方法上认识到高职数学建模是高等数学课程改革的一部分，最终目的是为学生将来进一步学习专业基础课、专业课及毕业后继续深造、终身学习打基础。在高等数学教学中，我们注重通过数学建模思想的渗透，培养学生的思维品质和数学能力，教会学生如何“用”数学，激发学生的探索精神和创新意识，增强学生的综合素质，从而成为一个素质全面、具有可持续发展的高技能人才[3]。高职数学建模作为高职数学理论与实践联系的桥梁不仅为高职数学的教学和教改提供了途径和方向，同时也为从事高职数学教育的专业技术人员提供了一个进行教学研究和教学改革的载体。

对学生而言，因为建模比赛中的赛题没有现成的答案，没有固定的方法，没有指定的参考书，没有规定的数学工具，甚至也没有成型的数学问题，主要靠学生独立思考、反复钻研并相互切磋，去形成相应的数学问题，进而分析问题的特点，寻求解决问题的方法，得到有关的结论，并判断结论的对错与优劣，这样就创造了一种学习和实践环境，使学生身临其境地介入数学的发现与创造过程，激发学生的学习兴趣，使学生觉得数学“学而有用”并真正“学以致用”，同时数学建模作为数学学习的一种新方式，它为学生提供了自主学习的空间，有助于学生体验数学在解决实际问题中的价值和作用，体验数学与日常生活和其他学科的联系，体验综合运用知识解决实际问题的过程，增强应用意识，使学生认识到：数学与我息息相关，与生活紧紧相连，解决问题的过程，就是探求未知的过程，更是培养创新精神和实践能力的过程[4];其次也培养了学生的其他各种能力，如提高了学生的认知能力，培养了学生的阅读能力、“双向”翻译能力，想象力、联想力，自学能力、使用文献资料的能力、计算机应用能力、论文写作与表达的能力，同时培养了学生良好的性格品质和初步形成了一定的数学精神。

4 高职数学建模的解题思路

4.1 高职数学建模赛题的来源

数学建模竞赛的题目由社会、经济、管理、生活、环境、自然现象、工程技术等领域中的实际问题简化加工而成，大多数是没有解决或无最优结果的实际问题，故无标准答案，结果灵活多样，可供参赛者发挥其聪明才智和创造精神。全国主委会每年提供四道赛题供参赛选手选择，A、B题的难度和范围高于C、D题，本科组只能选A、B题中的一题，高职组一般选C、D题中的一题，也可以选A、B题中的一题与本科组进行竞争。如表1为近几年数学建模的赛题。

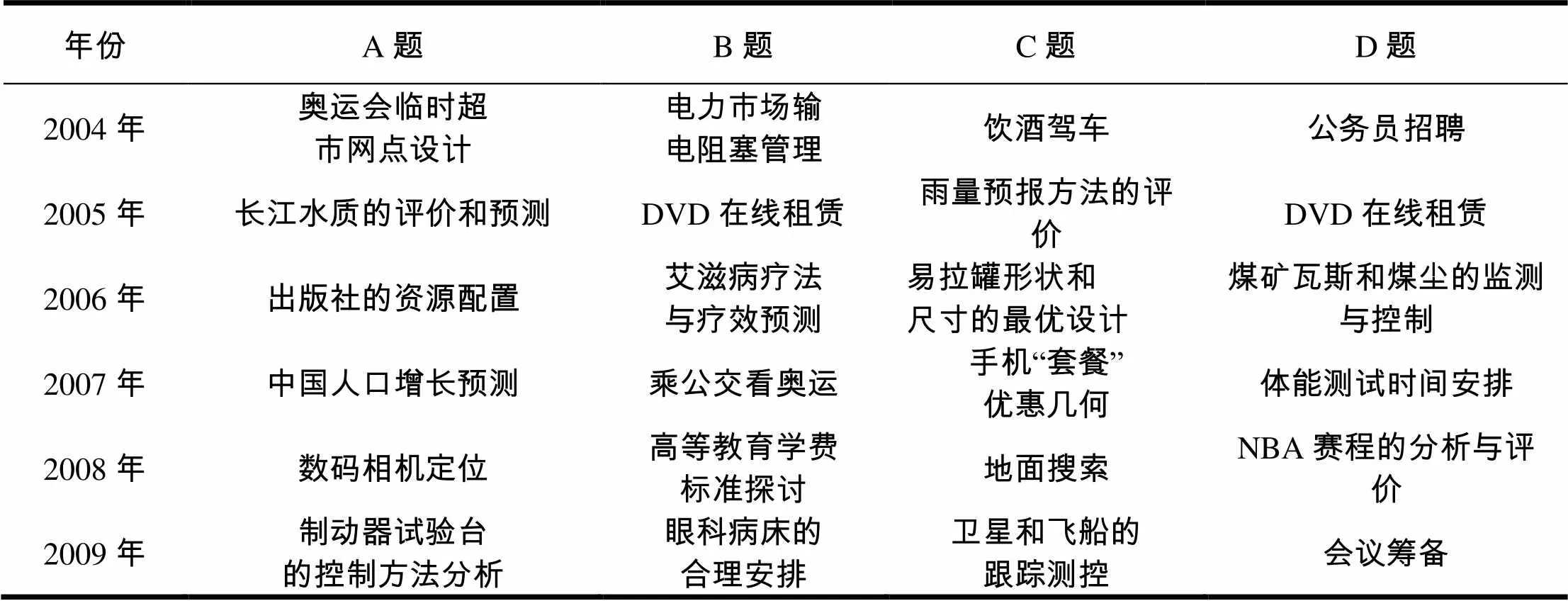
表1 近年数学建模的赛题

4.2 高职数学建模的分类

图4 高职数学建模的分类

4.3 高职数学建模的求解方法

图5 高职数学建模的求解方法

4.4 高职数学建模的求解过程

高职数学建模竞赛题目涉及的数学知识相比较本科组而言要简单狭窄，一般只包括初等数学、一元函数微积分、简单的数理统计和简单的数学规划（如线性规划、整数线性规划、0—1整数线性规划）等，并要求掌握相应的数学软件（Mathematica、Matlab、Lingo之一）的使用方法。以下为高职数学建模的求解过程流程图。

5 高职数学建模培训与参赛的思考

我国大学生数学建模竞赛经过十几年迅速、健康的发展，已经在国内外产生了很大的影响，树立起了自己的品牌，教育部也越来越重视高职技能竞赛，同时数学建模型竞赛对加快数学课程改革、提高学生数学应用能力起着重要的作用，但是参加高职数学建模的学校仍然很少，各高职院校对数学建模竞赛的培训力度和设施也较为不足。对福建省高职高专学校而言，数模竞赛规模也在日益扩大，从开始的三、四所学校参加到现在的二十多所学校参加。目前福建省高职类学生的参赛水平和培训力度以福建交通职业技术学院为最，我院分别在2007年和2009年的全国大学生数学建模竞赛取得国家二等奖和福建赛区一、二等奖，同时我院也多次参加了省数学建模大赛，取得较好的成绩，但我院学生的参赛水平和培训力度仍有很大的提升空间，具体体现在参赛选手的选拔和培训没有得到很好的展开，总是局限在一两个系并且培训的时间也比较少，当然这些都在逐步解决完善中。

对于高职数学建模的培训与参赛，个人认为着重参赛选手的选拔，可以先对全院进行海选，然后优中选优，能力与兴趣并重，全国数学建模大赛是三天三夜全力攻克一题，没有兴趣，哪能坚持，同时心态也非常重要，好高骛远者、眼高手底者必须排除在外；其次在培训上必须要有一个良好的培训环境，竞赛是三个人一个小组，参赛成员需要配合默契、分工明确、相辅相成，这些离不开平时的刻苦训练，同时一定要进行实战练习；最后就是考场的发挥了，数模题目没有最后的标准答案，这就需要学生的随机应变，此时就显现出平时培训的重要性了，但是此刻还有一个重要环节，就是三个人中必须有一个起主导作用的核心队长进行合理统筹安排，因此，在培训中，指导教师就要注意观察，发现具备较好大局观及统筹能力的学生，并有意识的进行指导培养，使其能在竞赛中发挥作用[5]。

[1]叶其孝.大学生数学建模竞赛辅导教材（五）[M]. 长沙：湖南教育出版社，2008：1－2.

[2]蒙诗德.浅论数学建模教学和竞赛活动中的创新教育[S].教育论坛，2010：95－96.

[3]靳永山.高职数学建模培训应处理好几个关系[J]. 天津职业院校联合学报，2009，11（5）：87－90.

[4]赵芳玲．学建模与学生综合素质的培养[J].西安航空技术高等专科学校学报，2006，24(5)：47－48.

[5]屈寅春.高职数学建模竞赛的实践[J].无锡职业技术学院学报，2008，7(4)：78－79.

Exploring teaching of mathematical modeling contest in higher vocational technology college

CAI Jian-gang

(Basic Teaching Division, Zhangzhou Institute of Technology, Fujian 363000,China)

The thesis discusses and analyzes the vocational background, present situation and solving thinking of mathematical modeling in Higher vocational technology college, Finally draws a conclusion :the mathematical modeling contest in higher vocational technology college must be selected and trained.

higher vocational technology college;mathematical modeling contest；solving thinking；training

2010－05－20

蔡建刚（1981－），男，助教，理学士，研究方向：应用数学。

G718.5

B

1673-1417（2010）03-0077-05