基于LS-DYNA软件的降落伞充气过程仿真研究
贾 贺,荣 伟,陈国良
(北京空间机电研究所, 北京 100076)
0 引言
降落伞系统作为一种高效、可靠的回收装置,在我国载人飞船、返回式卫星的回收着陆以及美国火星探测器的着陆等过程中,都得到了广泛的应用。充气是降落伞整个工作过程中最为复杂的一个阶段,也是研究人员迫切地想通过理论分析来解释的[1-2]。目前,对于降落伞充气性能(除最大开伞动载外)的了解或掌握主要是通过一些试验结果的统计分析来获取的,充气性能与开伞条件之间的关系也是通过试验结果统计、拟合出来的[3]。这使得充气时间、伞衣投影面积变化的一些经验公式存在着一定的局限性,只能在某些情况下适用。
随着“嫦娥一号”的成功发射,我国对于火星探测的研究即将进入实质阶段。火星大气层的成分、物理性质与地球的大气层存在着较大的差别,因此,对于降落伞系统在火星大气环境下的工作性能评定,不能像地球上回收航天器所用的降落伞系统那样可以通过空投试验来直接验证,而需要通过理论分析或者数值仿真来进行。目前回收系统工作过程的数值仿真系统所用到降落伞开伞过程的一些参数,如充气时间、伞衣投影面积的变化一般是采用经验公式来处理的。有关研究表明,对于火星这样稀薄的大气环境,这些常用的经验关系式将不再适用[4]。因此,如何通过数值仿真来获取研究降落伞充气过程性能的主要参数,已经被提上了降落伞理论研究和工程实践的日程。
进入21世纪以来,应用LS-DYNA有限元分析软件来分析降落伞的工作过程(充气阶段、稳定阶段等)成为一个热点。国外在这方面做了大量的工作,但是对降落伞充气过程的仿真还不能完全地解决[5-8]。国内使用 LS-DYNA软件对降落伞充气过程仿真研究尚属空白。本文基于LS-DYNA软件对数值模拟降落伞充气过程的方法进行了初步研究。
1 降落伞的充气过程
降落伞的充气过程是指从伞系统全长地拉直到伞衣第一次充满(伞衣投影直径第一次能达到稳定下降所需的伞衣投影直径,不考虑过度充气)为止的整个工作过程[1-2],如图1所示。
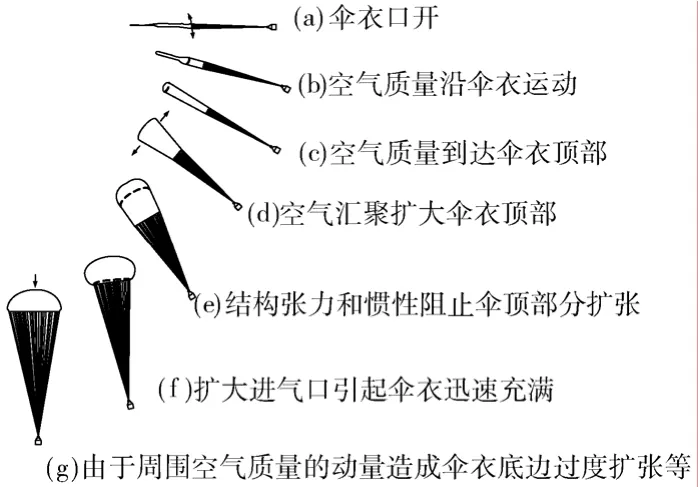
图1 降落伞的充气过程Fig. 1 Parachute inflation process
降落伞的充气性能主要由临界开伞速度、伞衣充满条件、充气时间、充气距离、伞衣投影面积变化和最大开伞动载等参数来描述和表征[1,3]。本文基于LS-DYNA软件对降落伞的充气时间和伞衣投影面积变化的数值模拟分析,来研究降落伞的充气过程。
2 LS-DYNA的流固耦合算法
LS-DYNA软件是著名的显式动力分析程序,具有强大精确的有限元仿真性能,拥有大量不同种类的单元模型、材料模型和算法选择,能够很方便地处理各种高度非线性问题。到目前为止,它是对降落伞充气过程进行仿真的最优工具之一。LS-DYNA 971是一个主要的程序版本。它增加了透气性材料的流固耦合算法,这样就可以通过控制流固耦合过程的各个参数,真实地模拟降落伞的充气过程。
LS-DYNA与一般的CAE辅助分析程序操作过程相似,LS-DYNA的一个完整的显式动力分析过程包括前处理、求解以及后处理3个基本操作环节,如图2所示。
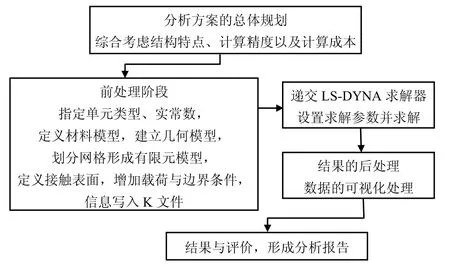
图2 LS-DYNA的一般计算流程Fig. 2 Computation process of LS-DYNA
在解决流固耦合问题时,需要一种将Lagrange和 Euler的优点结合起来的方法,即Arbitrary Lagrange-Euler,简称 ALE方法[9,10]。LS-DYNA程序中采用关键字*CONSTRAINED_ LAGRANGE_IN_SOLID实现固体与流体间的耦合。采用流固耦合算法模拟问题时,往往要对Lagrange算法中的固体结构进行约束,将固体结构的相关参数传递给流体单元。在LS-DYNA中数值模拟降落伞的充气过程时,固体结构的主要约束方法是罚函数耦合约束。对于罚函数约束而言,其原理是耦合系数追踪Lagrange节点(结构,即从物质)和Euler流体物质(主物质)位置间的相对位移d,如图3所示[11]。
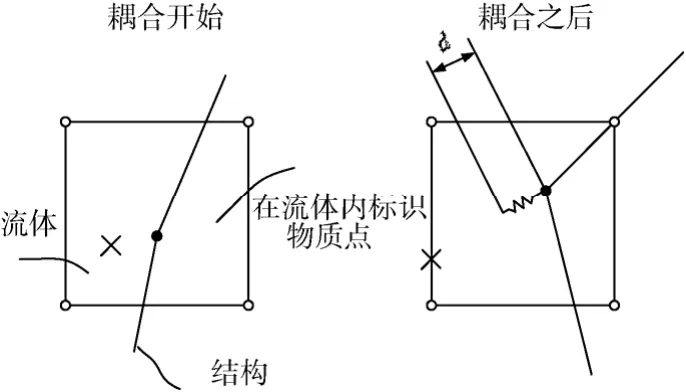
图3 罚函数耦合算法Fig. 3 Penalty function coupled method
3 LS-DYNA仿真模型的建立
3.1 降落伞仿真模型的建立
3.1.1 基本假设
对降落伞仿真模型作如下假设:
1)仿真充气过程前模型为轴对称的结构;
2)模型的初始形状为有一定的进气孔尺寸,截面为梅花形状的模型;
3)模型只考虑伞绳的连接,对于伞衣径向带、顶孔绳等不作具体处理。
3.1.2 基本参数设置
1)降落伞几何模型
降落伞仿真模型选用美国的经典伞型—C-9平面圆形伞,如图4(a)所示,具体结构参数如表1所示。
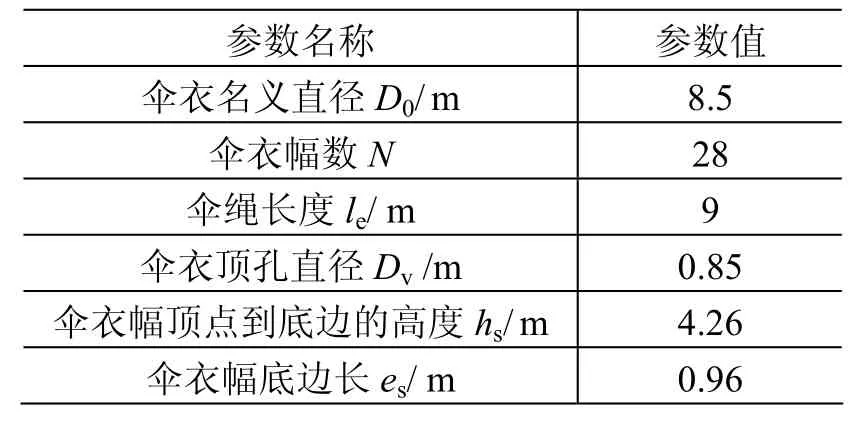
表1 C-9伞结构参数表Table 1 Structure parameters of C-9 parachute
完整的伞衣和伞绳几何模型如图4(b)所示。
2)材料参数的选择
降落伞仿真模型的伞衣材料选用美军标的MIL-C-7020 III材料,假设该材料为各向同性材料,密度为533.77 kg/m3,弹性模量为0.4309 GPa,泊松比为0.14,伞衣厚度为0.000 1 m。伞绳材料的密度为462.00 kg/m3,弹性模量为97.0 GPa。假设降落伞伞绳的横截面为圆形,面积为4.91×10-6m2。
3)网格的划分
LS-DYNA的前处理软件用于对降落伞仿真模型进行有限单元的网格划分。伞衣单元选用薄壳单元,伞绳单元选用离散的梁/索单元,得到降落伞的有限元模型如图4(c)所示。

图4 降落伞模型Fig. 4 Parachute model
4)K文件的参数设置
降落伞仿真模型的伞衣单元为薄壳单元(*ELEMENT_SHELL_THICKNESS),单元算法的控制关键字为*SECTION_SHELL。伞衣材料属性由*MAT_FABRIC关键字来定义。伞绳为离散的梁/索单元(*ELEMENT_BEAM),单元算法的控制关键字为*SECTION_BEAM。伞绳材料属性由*MAT_CABLE_DISCRETE_BEAM来定义。
伞绳汇交点采用关键字*BOUNDARY_ SPC_NODE来进行约束,即对汇交点的3个方向平动自由度进行约束。
5)求解文件的生成
降落伞仿真模型建立完成,生成LS-DYNA软件可以求解的文件格式,记为K文件(parachute.k)。
3.2 流场仿真模型的建立
3.2.1 基本假设
对流场仿真模型作如下假设:
1)流场模型模拟的为不可压缩流场,符合N-S方程;
2)流场模型中流体的速度方向恒定,且速度大小不变;
3)流场模型外表面的边界约束条件与风洞壁性质一致。
3.2.2 基本参数设置
1)流场几何模型
流场仿真模型形状选用圆柱形流场,如图5(a)所示。综合文献[12−14],其基本的几何尺寸确定如下:流场半径 Df=12 m;流场长度 Lf=31 m;流场前端面距伞绳汇交点的长度Lq=6 m;未充气流场后端面距伞衣顶端的长度Lh=12 m。
运用LS-DYNA的前处理软件建立流场几何模型如图5(b)所示,流体速度为80 m/s。
2)材料参数的选择
流场仿真模型的流体定义为理想气体,满足理想气体状态方程。气体的密度为1.18 kg/m3,动态粘度系数为1.745 6×10-5,气体的比热容比为γ=1.4。
3)网格的划分
同样,在LS-DYNA前处理软件中对流场的几何模型进行有限单元的网格划分。根据有限元网格划分的基本原则,流场的有限元模型如图 5(c)所示。

图5 流场模型Fig. 5 Fluid model
4)K文件的参数设置
流场仿真模型的单元选择体单元(*ELEMENT_ SOLID),流场仿真模型单元算法的关键字为*SECTION_SOLID。LS-DYNA要想真实地模拟降落伞的充气过程,必须在流场前端增加一层流体压力入口单元,主要作用是向流场中源源不断地输入恒压、恒速的流体。流场单元算法参数的选择对于解决流固耦合问题很关键,本文为流体单元选择的是单点ALE方法的多物质单元方程。对于已定义关键字*MAT_NULL的材料而言,必须包含状态方程的定义,用来提供压力行为应力组件,表示材料的体积变形与压力之间的关系。这样两者合起来提供材料的整个应力张量。流体仿真模型的状态方程用*EOS_LINEAR_POLYNOMIAL来定义。
流场仿真模型的流场入口单元区域用*BOUNDARY_PRESCRIBED_MOTION_SET来施加对单元的强制运动,使得流体压力入口单元获得恒定的速度。
5)求解文件的生成
流场仿真模型建立完成,最后生成LS-DYNA软件可以求解的文件格式,记为K文件(fluid.k)。
4 LS-DYNA流固耦合控制参数
LS-DYNA软件是一种比较理想的显式求解工具,通过它的前处理器,生成一个可以递交给LS-DYNA的文件,称之为关键字文件或K文件,该文件是由一系列的关键字组成的[15]。LS-DYNA求解流固耦合问题,实质上就是对流固耦合控制关键字进行参数设置的过程。
但是,降落伞充气过程与一般的流固耦合问题不完全相同,如果按照一般的流固耦合问题处理,仅仅设置一般问题的基本控制关键字来仿充气过程,可以发现伞衣没有完全充开,最终的充气形状也很不理想,如图 6所示。可见,使用LS-DYNA对充气过程进行仿真时,不能仅仅采用一般问题的解决方法和思路,必须选择适合充气过程的控制关键字,并对关键字进行参数值的优化处理。

图6 基本控制参数下的伞衣最终充气形状Fig. 6 Final canopy shape with basic control parameters
通过大量的研究分析,得到在仿真降落伞充气过程中,主要的流固耦合过程控制关键字及最优化的控制参数值,其中主要的控制关键字如表2所示[16]。可见,选择适合降落伞充气过程的控制关键字及设置最优化的参数值是仿真充气过程的重点和难点,对仿真过程的实现起着决定性作用。

表2 流固耦合过程的主要控制关键字Table 2 Major keywords of Fluid-Structure Interaction(FSI) process
5 降落伞充气过程的仿真结果及分析
5.1 降落伞充气过程的数值模拟
图7中(a) (i)表示的是在LS-DYNA中数值模拟降落伞充气的全过程。
可以很清楚地看到,在充气开始的时候,降落伞的充气形状变化比较慢。在0.02 s时,气流使得降落伞的伞衣顶部开始发生形状的变化;从0.02 0.10 s,伞衣顶部变化显著,气流将整个降落伞的顶部完全顶开。从0.10 0.16 s,气流从伞衣顶部向伞衣周围流动,使得伞衣的充气形状不断发生变化;在0.16 s时,降落伞充气达到最大外形形状,即达到充满状态。从0.16 0.18 s降落伞的充气形状发生一次较为明显的收缩。从0.18 0.26 s降落伞的充气形状会不断发生微小的变化,伞衣产生较为明显的“呼吸现象”。通过对伞衣充气形状的测量,发现在0.26 s时降落伞的充气过程基本完成。

图7 LS-DYNA数值模拟的降落伞充气过程Fig. 7 Parachute inflation simulation with LS-DYNA
5.2 降落伞的充气时间
5.2.1 充气时间的理论求解
基于 LS-DYNA对降落伞充气过程的数值模拟,其实就是对降落伞做类似于风洞试验的研究。因此,数值模拟降落伞的充气过程是一个无限质量条件下的充气过程。可通过理论方法求解无限质量条件下C-9平面圆形伞的充气时间tf。
[17,18]可知,对于无限质量条件下的致密织物的降落伞充气过程而言,降落伞的充气时间指的是伞衣第一次达到最大外形状态的时间。
设降落伞的名义直径为D0,有效透气量为C,开始充气时的速度为 v0,无因次充气时间为 T0,对于基本方程

而言,当考虑无限质量条件充气时,可以把速度 v看作一个常数,并且等于充气开始时的速度v0,则基本方程可以直接积分。把上述方程写成积分形式为
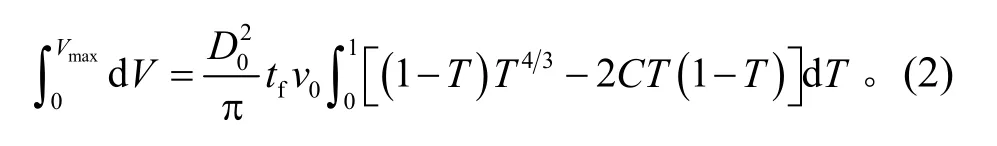
如果只考虑名义直径为D0的平面圆形伞,并假设降落伞伞衣在完全充满时呈半球状,则有

式中Vmax为降落伞伞衣充满时所包容的空气体积。
对式(2)进行积分,并把式(3)代入,得到充气时间的表达式
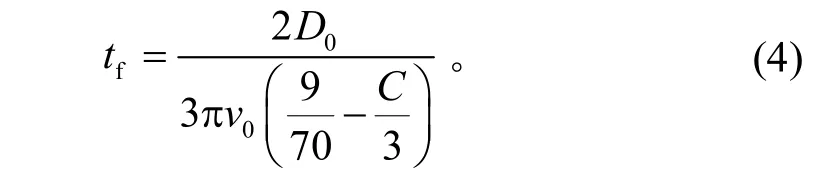
已知降落伞的名义直径D0、有效透气量C和降落伞开始充气时的速度v0,就可以直接计算出在无限质量条件下降落伞的充气时间 tf。数值模拟充气过程的C-9伞的名义直径D0为8.5 m,开始充气时的速度v0为80 m/s,故求解降落伞的充气时间转化为求解其有效透气量的问题。由于C-9伞伞衣材料选用的MIL-C-7020 III型材料,由图8所示的曲线,可以得到其压差和有效透气量的关系。

图8 MIL-C-7020 III材料压差与有效透气量曲线Fig. 8 MIL-C-7020 III material pressure vs effective permeability
由于模拟无限质量条件下的充气过程可看作为风洞试验,大气密度ρ为1.18 kg/m3,则压差为

由图8可知,C-9伞伞衣的有效透气量C约为0.09。由式(4)计算出其在无限质量条件下充气时间为tf=0.21 s。
5.2.2 充气时间的数值模拟值与理论求解值的比较分析
数值模拟 C-9伞伞衣第一次达到最大外形状态的充气时间为0.16 s,这与理论求解的充气时间0.21 s的偏差为23%,是在可接受的范围之内。并且数值模拟充气过程时,可以求解得到伞衣最终达到稳定状态时的充气时间为0.26 s。
5.3 降落伞的投影面积变化
5.3.1 投影面积变化的数值模拟
数值模拟的 C-9伞伞衣底边投影面积的形状变化如图9所示。

图9 伞衣底边投影形状的变化Fig. 9 Canopy project shape variations
5.3.2 数值模拟与试验结果的比较分析
从充气过程开始到伞衣最终达到稳定状态,数值模拟 C-9伞充气过程的伞衣投影面积比随充气时间的变化情况。如图10(a)所示,C-9伞充气过程的伞衣投影面积比随无因次充气时间的变化如图10(b)所示。

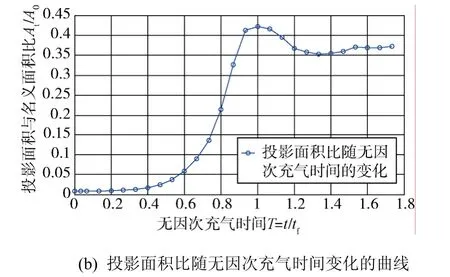
图10 伞衣投影面积比的变化Fig. 10 Canopy project area ratio variations
由图 10(b)中可以看出,伞衣投影面积随着充气时间的延长而不断增加,在T=1时达到最大值,投影面积与伞衣名义面积之比为 0.42。而在 T=1之后伞衣有一个明显的收缩过程。而从图 10(a)可以更加清楚地看到,在tf=0.21 s时,伞衣的投影面积变化趋势基本稳定,虽然由于伞衣的“呼吸现象”会使得伞衣的投影面积产生一些微小的变化,但是在tf=0.21 0.26 s之间,可以认为伞衣的投影面积不再发生变化,即降落伞达到充满稳定状态。
与 D0=8.5 m的平面圆形伞试验结果[1]对比可以发现,数值模拟C-9平面圆形伞充气过程的伞衣投影面积变化规律与试验得到的变化规律基本一致。在达到充气时间时,试验的伞衣投影面积与名义面积比为0.4,数值模拟的伞衣底边投影面积与名义面积比为0.42,面积比基本相等。可见,数值模拟降落伞充气过程,得到的伞衣投影面积的变化情况与试验得到的结果基本一致。
6 结束语
本文基于 LS-DYNA软件对降落伞的充气过程进行了数值模拟,得到了降落伞的充气时间和投影面积变化的规律,并对这些主要参数进行了分析,验证了使用 LS-DYNA软件模拟充气过程的可行性,为降落伞的设计及其性能分析提供了一种新的分析手段。由于流固耦合过程控制关键字的参数值还没有完全达到最优化,导致降落伞充气时间的误差较大,这也是下一步工作需解决的主要问题。
参考文献(References)
[1] 王利荣. 降落伞理论与应用[M]. 北京宇航出版社, 1997
[2] 《降落伞技术导论》编写组. 降落伞技术导论[M]. 北京: 国防工业出版社, 1977
[3] Ewing E G, Bixby H W, Knacke T W. 回收系统设计指南[M]. 北京: 航空工业出版社, 1988
[4] 荣伟. 火星探测器减速着陆技术研究[D]. 中国空间技术研究院博士学位论文. 北京: 中国空间技术研究院, 2008
[5] Taylor A P. An investigation of the apparent mass of parachutes under post inflation dynamic loading through the use of fluid structure interaction simulations, AIAA 2003-2104[R], 2003
[6] Benjamin A T, Anthony P T. The use of LS-DYNA to simulate the inflation of a parachute canopy, AIAA 2005-1608[R], 2005
[7] Benjamin A T, Anthony P T, Jean C B, et al. The use of LS-DYNA to assess the performance of airborne system North America candidate ATPS main parachutes, AIAA 2005-1609[R], 2005
[8] Benjamin A T. The application of a new material porosity algorithm for parachute analysis[C]//9thInternational LS-DYNA Users Conference, 2006
[9] 李裕春, 等. ANSYS 11.0/LS-DYNA 基础理论与工程实践[M]. 北京: 中国水利水电出版社, 2008
[10] 赵海鸥. LS-DYNA 动力分析指南[M]. 北京: 兵器工业出版社, 2003
[11] John O H. Theoretical Manual[M]. Livermore Software Technology Corporation(LSTC), 1998
[12] Lingard J S, Darley M G. Simulation of parachute fluid structure interaction in supersonic flow, AIAA 2005-1607[R], 2005
[13] Lingard J S, Darley M G, Underwood J C. Simulation of Mars supersonic parachute performance and dynamics, AIAA 2007-2507[R], 2007
[14] Christine Espinosa, Yves de Lassat de Pressigny, Pascal Bordenave, et al. Fluid-structure interaction simulation of parachute dynamic behaviour, AIAA 2007-2510[R], 2007
[15] Livermore Software Technology Corporation(LSTC). LS-DYNA keyword user’s manual[G]. Version 971, 2007
[16] 贾贺. 基于LS-DYNA的降落伞充气过程研究[D]. 中国空间技术研究院硕士学位论文. 北京: 中国空间技术研究院, 2009
[17] 彭勇, 宋旭民. 降落伞充气时间的计算方法[J]. 航天返回与遥感, 2004, 25(1): 17-20
[18] 返回技术翻译组. 气动力减速器原理及设计手册(上册)[M]. 北京: 国防工业出版社, 1976

