市场环境及 CO2排放政策变化下的发电投资决策*

刘国中 文福拴 董朝阳

(1.华南理工大学电力学院,广东广州 510640;2.昆士兰大学,昆士兰 4067,澳大利亚)

电力工业市场化改革后,发电投资成为投资者以自身利益最大化为目标的投资行为.与传统的发电投资规划相比,在电力市场环境下,发电投资面临着更多的不确定性因素带来的风险,如负荷、电价和燃料价格的不确定性等[1].另一方面,温室气体尤其是CO2的排放对气候变化的影响,乃至全球气温变暖已成为很多国家尤其是发达国家所关注的重要问题.在国际上,已经有了一些气候变化政策和协议,旨在对 CO2等温室气体的排放进行限制[2].在上述背景下,投资者在进行发电投资决策时,如何适当计及与电力市场和排污限制措施有关的不确定性因素的影响以规避相关风险就成为需要研究的重要问题.

目前已有不少文献研究了在存在多个竞争者的环境中的投资决策问题和投资均衡状态[3-7].文献[3]中基于离散马尔可夫链模型,研究了完全竞争条件下的投资均衡问题;文献[4]中则在假定需求随机变化的基础上,利用随机控制理论,研究了社会效益最优和投资者效益最优之间的关系.然而,这些模型所基于的假设在很大程度上限制了它们的实际应用.首先,这些模型均假设外部环境是完全竞争的市场环境;而事实上,不少行业由于对资金或技术要求较高,存在较大的进入壁垒,往往只能形成少数几个寡头垄断企业,而非完全竞争的市场.其次,这些模型中假设投资规模可连续递增;实际上,由于技术限制和生产成本的原因,企业生产规模扩张一般都是离散的,大部分是以增加生产模块的形式来实现.例如,发电投资只能通过增加一台或多台具有一定容量标准的发电机组来实现.发电投资领域具有典型的寡头垄断特征,这样,发电投资决策问题事实上属于寡头垄断企业之间的寡头博弈问题,适于采用期权博弈理论来研究[5].

在上述背景下,文中研究了在给定的规划周期内,发电公司或投资者在面临多个不确定性因素(燃料价格、负荷水平、排污限制政策)以及其它发电公司可能投资的情况下的投资决策问题.建立了计及多种不确定性因素的发电投资的期权博弈模型框架,在假定发电投资依次进行的前提下,发展了基于Barraquand-Martineau(B-M)期权定价模型的求解方法,并通过算例对所提出的方法进行了说明.

1 期权博弈模型框架

假设电力市场中存在m个发电公司,均计划在规划期 [T1,Tn]之间的某一子周期内投资新建电厂.对任意的发电公司 k,计划兴建的电厂容量为CkMW,投资资金为Ik美元.这里,T1表示从当前开始的第一个规划子周期.在[T1,Tn]之间的任意子周期,发电公司 k可以自由选择立即投资、等待或者永远放弃该投资计划.由于发电公司 k可以在给定时间内的任意子周期执行投资计划,因此其投资机会可被看作是一个美式看涨期权.投资项目在各个子周期的价值相当于标的资产的价值,投资费用Ik相当于期权的执行价格.Tn为投资计划可被执行的最后子周期,其相当于期权的到期日.

对发电公司k而言,其投资决策就是针对所研究的规划周期内,在面临将来诸多不确定性因素的条件下,选择最佳的投资时机来最大化自己的收益.不确定性因素包括将来的燃料价格、系统负荷、发电容量充裕性水平、将来的市场电价以及CO2的排放价格等.其中,将来的市场电价与系统负荷及系统容量充裕性水平之间存在着一定的关系[8].当系统负荷较高,容量充裕性较低时,市场电价往往较高,反之亦然.系统的发电容量充裕性水平则和其它发电公司的投资行为密切相关.因此,文中将发电公司k投资决策过程中所面对的不确定性因素归纳为以下4个方面:①未来燃料价格的变化;②未来的负荷水平;③未来CO2的排放价格;④其它发电公司的投资决策(表现为系统装机容量的变化).其中,前3个因素采用随机过程来模拟,而第 4个因素则通过在整体投资决策模型中引入动态博弈过程来计及.

1.1 不确定性因素的随机变化模型

采用文献[9]中提出的模型,未来燃料价格的变化可表示为

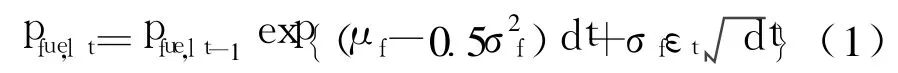
式中:pfuel,t为第t(t=T1,T2,…,Tn)个规划子周期的燃料价格;μf为燃料价格的期望增长率;σf为燃料价格增长率的标准差;εt服从标准正态分布,即εt～N(0,1);dt为单步时间步长,对于文中所研究的问题,dt为规划子周期的长度.

与燃料价格类似,系统最大负荷的变化可表示为

式中:Lmax,t为第t个规划子周期的最大负荷,MW;μL为最大负荷增长率的期望值,%;σL为最大负荷增长率的标准差,%.

类似地,CO2的排放价格可表示为

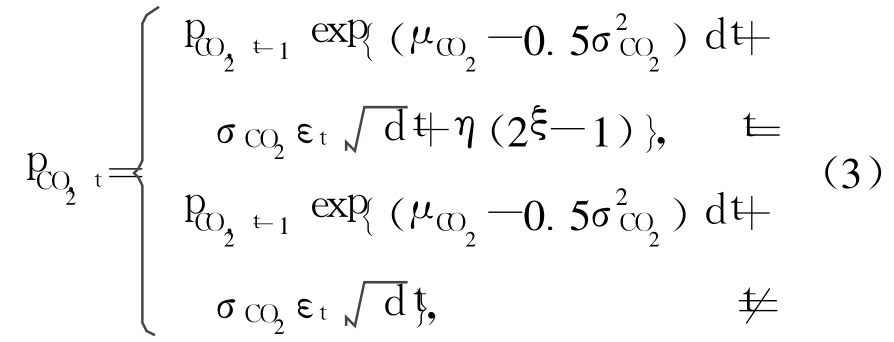
式中:pCO2,t为第t个子周期内CO2的排放价格;μCO2为CO2排放价格增长率的期望值,%;σCO2为CO2排放价格增长率的标准差,%;ξ为[0,1]区间均匀分布的随机变量,这样pCO2,t(2ξ-1)表示CO2排放价格变化范围为±100%;η为比例因子.

1.2 发电公司投资决策的随机动态模型

当计及发电公司投资行为间的相互影响时,发电投资决策将是一个动态博弈均衡过程.因此,在计及前文所述的 4种不确定性因素的情况下,所研究的发电公司 k的投资决策过程可用如下的随机动态模型来描述:

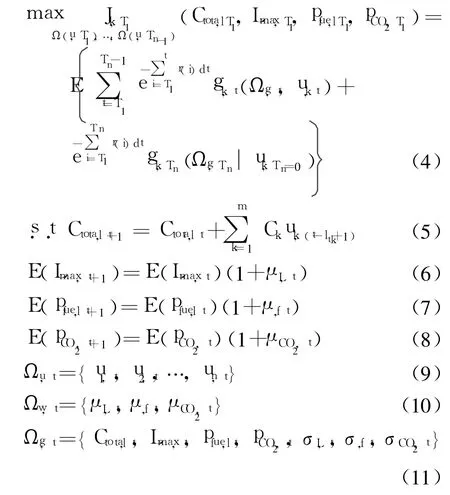
式中:目标函数为整个规划周期内发电公司 k期望的最大累积收益折算到子周期T1的净现值;r(i)为第i个子周期内的无风险利率;uk,t为公司k在第t个子周期的投资决策,其为 0-1变量;如进行投资,则uk,t为1,否则为0;gk,t为公司k在第t个子周期的期望净收益;gk,Tn为公司k在最后一个子周期Tn内的期望净收益;Ctotal,t为第 t个子周期的系统总装机容量;ltk为公司k建设新电厂所需的时间;Ωu,t为第t个子周期内所有发电公司的投资决策集合;Ωw,t表示不确定性因素在第 t个子周期内的变化趋势集合(即期望增长率的集合);Ωg,t为影响第t个子周期收益函数g的因素集合.

2 求解方法

对于式(4)～(11)所描述的动态随机博弈问题,一个直接的求解思路就是推导每个发电公司最优化问题的Karush-Kuhn-Tucker(KKT)条件,如此可以将问题转化为非线性互补问题(NCP),然后用改进的Levenberg-Marquard t算法对其进行求解[10].然而,当数学模型中包括时间变量和随机因素时, NCP问题的搜索空间将呈指数增长,对于大规模问题存在维数灾问题.

为简化问题并考虑到发电投资问题的实际情况,这里做如下假设.

假设:在规划周期内的任意子周期,至多只有一个发电公司进行投资,当市场条件可能触发多个发电公司的投资行为时,期望投资回报率最高的发电公司会率先投资;换言之,发电公司的投资行为将会依次进行.

只要子周期比较短,这个假设就是合理的.此外,较长的规划周期也使得发电公司有很多投资机会,当已有电厂正在投资建设时,如其建设周期较短,其它发电公司会倾向于等待将来的市场信息更明确后再进行投资.

这里假定每个规划子周期的时长为2年(燃煤电厂或燃气电厂的建设通常可在 2年内完成),这样可保证在上一个子周期建设的电厂,在接下来的子周期内可投入生产.

2.1 发电公司投资顺序的确定

当所研究的规划周期较长且系统内的发电公司数目有限时,可以认为发电公司都会先后实施其投资计划,并假设投资顺序为 k1,k2,…,km.在此情况下,可采用回溯法来确定每个发电公司的投资顺序.具体步骤如下所述.

(1)确定最后投资的发电公司km.

当最后投资的发电公司 km进行投资时,博弈已经结束,其它发电公司均已完成投资,其相当于拥有一个永久美式期权.可利用文献[8]中介绍的B-M实物期权定价模型来确定发电公司 km的最佳进入时机.发电公司km可用如下方法确定:从现有的m个公司中随机选取一个发电公司 k,假定其为最后投资者,其余m-1个公司均已投资,用B-M实物期权定价模型来确定其最佳进入时机tk*和投资收益触发区块j以及区块j对应的市场状态区块jΩ(具体过程见2.2节).在此过程中系统装机容量为恒定为系统初始装机容量,则对应的就是最后投资的发电公司对应多个发电公司,则比较触发投资的市场状态区块 jΩ是否相同,若不相同,则表明不同的市场状态会导致不同的发电公司成为最后投资者;若相同,则进一步比较发电公司的投资回报率,最高者即为发电公司km.

(2)确定倒数第二个投资的发电公司km-1.

在剩余的m-1个发电公司中,按(1)中的方法可确定倒数第二个投资的发电公司km-1的最佳投资时机和相应的投资收益.需要指出,发电公司k-1的收益应分两部分来计算:在子周期m之后,系统装机容量为时的收益和在子周期及之前,系统装机容量为收益.

(3)其余发电公司的投资顺序可类推得到.

2.2 计算投资时机和收益的主要步骤及方法

利用B-M实物期权定价模型进行发电投资决策的主要步骤和方法如下:

(1)负荷变化路径的模拟.根据式(2)进行X次蒙特卡罗随机抽样.每一次抽样形成一个完整的负荷变化路径,从而得到第 t个子周期内的最大负荷Lmax,x,t(x=1,2,…,X;t=T1,T2,…,Tn).这里,X为给定的足够大的正整数.

(2)燃料价格和 CO2排放价格变化路径的模拟.根据式(1)和(3)分别进行Y次和Q次蒙特卡罗随机抽样.对于每一次抽样,均形成一个完整的变化路径,即pfuel,y,t、pCO2,q,t(y=1,2,…,Y;q=1,2,…,Q; t=T1,T2,…,Tn).这里,Y和Q均为给定的足够大的正整数.

(3)利用B-M模型计算发电公司k的最佳投资时机.

(a)路径区块的划分.对于第t个子周期,首先按照由大到小的顺序将最大负荷排序、按由小到大的顺序将燃料价格和CO2排放价格进行排序(因为负荷越大,越容易触发投资;燃料价格和 CO2排放价格则相反,价格越低,越容易触发投资);然后将所有路径平均分配到JX、JY和JQ个区块中(JX、JY和JQ分别为设定的最大负荷、燃料价格和CO2排放价格区块的个数),使得每个区块中都包含相同的路径数.这样,每个最大负荷、燃料价格和CO2排放价格区块包含的路径数分别为NJX=X/JX,NJY=Y/ JY,NJQ=Q/JQ.

从JX、JY和JQ中分别抽取一个区块jX、jY和jQ,给定jΩ={jX,jY,jQ},则jΩ为包含了3种不确定性因素的区块.

(b)转移概率的计算.首先统计出所有在子周期t属于区块jΩ而在子周期t+1属于区块hΩ的路径数 bt,jΩ,hΩ,进而可得到在子周期 t属于区块 jΩ而在子周期 t+1转移到区块 hΩ的概率 ζt,jΩ,hΩ

式中:NJΩ=NJXNJYNJQ,JΩ=JXJYJQ,JΩ为区块jΩ的个数.

(c)子周期内不同市场状态下的投资收益区块的划分.首先计算第t(t=T1,T2,…,Tn)个子周期内区块jΩ中最大负荷、燃料价格和CO2排放价格的平均值,并以此表示区块 jΩ所代表的市场状态,则每个子周期中将有JΩ个市场状态.然后,针对所采用的电力市场模式,计算出发电公司 k在第t个子周期内任意区块jΩ的投资收益 gt,jΩ(具体过程见第 3节).之后,按照由大到小的顺序将投资收益gt,jΩ进行排序,并平均分配到J个区块中(J为设定的收益区块个数).每个投资收益区块j的收益可以表示为区块内投资收益的平均值,记为. 同时,记录每个子周期内投资收益区块j与市场状态区块jΩ的映射关系,并根据式(12)确定投资收益区块j在各个子周期内的转移率 ζt,j,h.

(d)投资收益 VTinv,j的计算.定义VT,j为发电公司k在子周期T中的区块j的累计收益,其表示在[T,Tinv+Tlf]之间可以获得的投资总收益.这里,Tinv表示发电公司的投资时间,Tlf为电厂寿命.

这样,子周期 T中每个区块的累计收益为

式中:Vr,j为投资项目的剩余收益.为简化分析,假设在规划期Tn以后至电厂寿命结束前的任意子周期时长内的投资收益均这 样剩余收益为

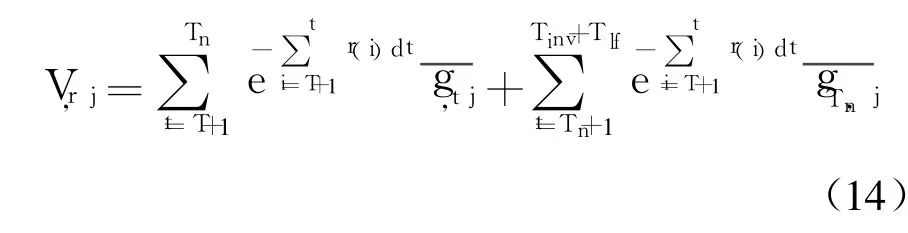
在求得子周期T中所有区块的累计收益后,采用回溯方法并利用上一步计算得到的转移概率,可求得发电公司在t=T-1,T-2,…,Tinv+1的每个子周期中的各个区块所能获得的累计收益:

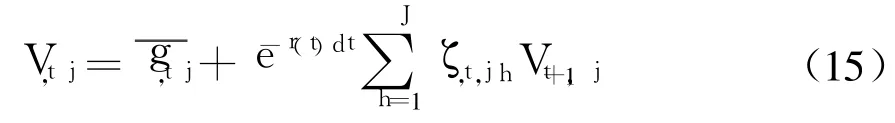
进一步回溯可求得发电公司在子周期Tinv的任意区块投资时的期望总收益VTinv,j.

(e)期权价值的计算和投资决策.在子周期Tn时,如果投资项目的期望总收益大于投资成本,则发电公司k将执行该投资项目,反之将放弃该投资项目,从而该规划期中每个区块的期权价值等于max{VTn,j-Ik,0};对于[T1,Tn-1]各子周期中各个区块的期权价值 Ft,j,可采用回溯方法通过比较立即执行投资的项目价值与持有期权继续等待的价值来确定,即:

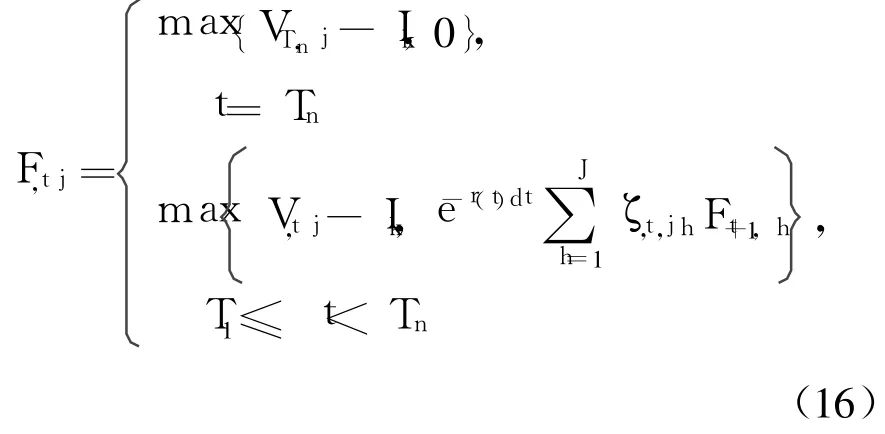
用LTn,j表示在子周期Tn的区块j中的期权执行情况,Lt,j表示在子周期t(t=T1,T2,…,Tn-1)的区块j中的期权执行情况:

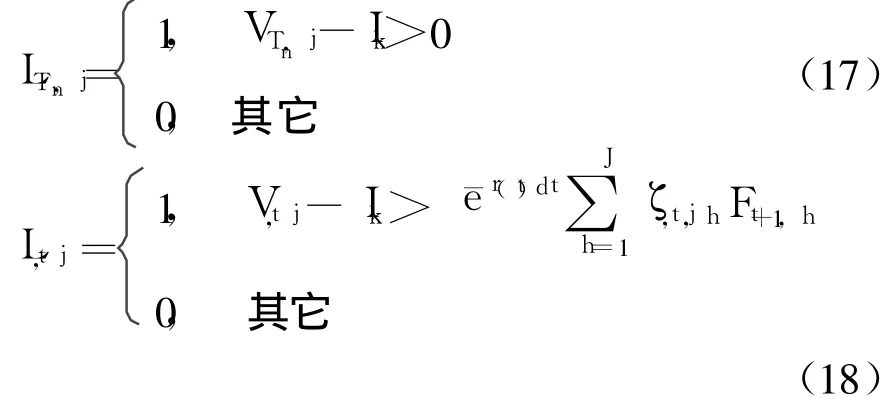
式中:“1”和“0”分别表示期权被执行和不被执行.

发电公司k为了最大化自己的投资收益,会选择在 Lt,j首次为 1时立即执行该投资计划,相应的时间即为最优投资时机tk*.在最优投资点到来以前, Lt,j均为 0,这意味着此时的最优选择为“持有期权继续等待”.

3 发电公司投资收益计算

假设发电公司k可从现货(日前)市场获得售电收益和装机容量市场获得容量收益,则其在子周期t中的任意区块jΩ的收益可表示为

式中:πen,t,jΩ和 πcap,t,jΩ分别为发电公司k在现货(日前)市场获得的售电收益和在装机容量市场获得的容量收益.

文献[8]中通过对PJM电力市场的日前能量市场在 2001年的每周加权平均电价与每周平均装机容量水平的历史数据进行了统计分析,发现采用三次函数来描述每周加权平均电价(pe,t,w)与每周平均系统容量裕度之间的关系比较合适.这里沿用文献[8]中的方法,假设在子周期 t内的每周加权平均电价满足如下关系:

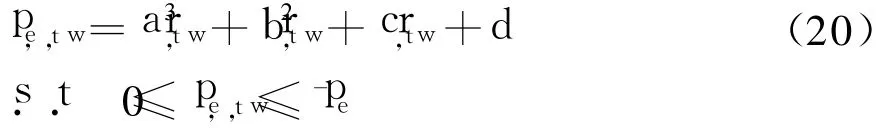
式中:a、b、c和d为电价预测模型的常量系数,在下面的分析中,给定它们的取值分别为:a=-776, b=1322,c=-748.8,d=142.pe,t,w为子周期t内第w周的加权平均电价,美元◦(MW◦h)-1;rt,w=(Ct,w-Lt,w)/Ct,w,其表示在子周期 t内第 w周的平均系统容量裕度;¯pe市场监管机构为防止发电公司滥用市场势力而确定的价格上限;Lt,w为从子周期 t内区块jΩ得到最大负荷 Lmax,t后,由典型的历史曲线得到的每周平均负荷;Ct,w为子周期t内第w周的平均装机容量水平,MW,这里假设其在子周期t内保持不变.

在采用式(20)求得每周加权平均电价pe,t,w后,发电公司k在现货(日前)市场所能获得的收益为

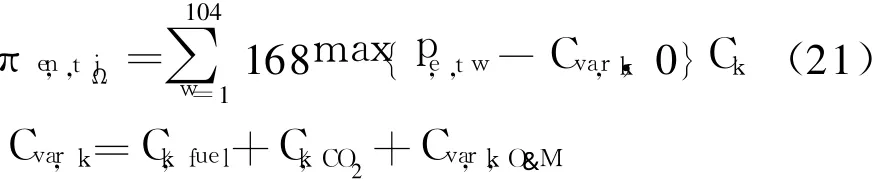
式中:Cvar,k为电厂的单位可变成本,美元◦(MW◦h)-1; Ck,fuel为生产单位电量的燃料成本,美元◦(MW◦h)-1; Ck,CO2为生产单位电量的CO2排放成本,美元◦(MW◦h)-1; Ck,fuel和 Ck,CO2均可由区块 jΩ得到;Cvar,k,O＆M为电厂单位电量的运行和维护成本,美元◦(MW◦h)-1.式 (21)假定了发电机组要么满出力发电,要么在价格低于其可变成本时不发电.采用这样的假设只是为了便于说明所提出的方法的基本特征,文中所发展的方法框架并不局限于这种特殊情形,事实上可以处理任意情形.

类似地,假设装机容量市场未来的价格遵从下述关系:

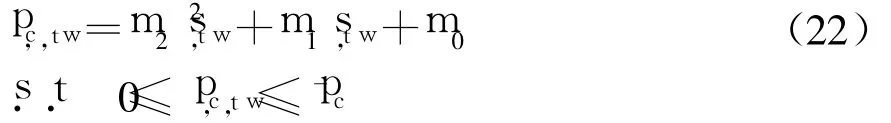
式中:st,w=(Ct,w-CR,t)/Ct,w表示子周期t内第w周装机容量充裕度;CR,t=Lmax,t×115%表示由监管机构确定的容量责任总量,假定为系统最大负荷的115%;¯pc为由监管机构确定的装机容量价格上限,美元◦(MW◦d)-1;m0、m1和m2均为常系数.在下面的分析中,给定它们的取值为[3]:m0=181,m1= -164,m2=-146.27.

这样,发电公司k在装机容量市场所能获得的容量收益为

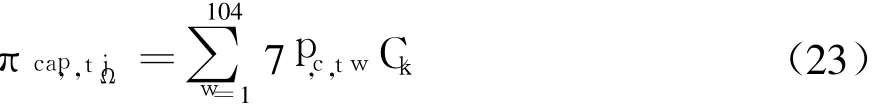
4 算例

假设在所研究的电力系统中,有 3家处于寡头垄断地位的发电公司A、B和C,这3家公司均计划在[0,19]年间投资新建电厂.假设每个规划周期为2年,这样就共有 10个规划周期.其中,发电公司A、B和C分别拟新建常规的燃煤电厂、带有碳捕获和储存装置(CCS)的燃煤电厂和天然气发电的燃气蒸汽联合循环(CCGT)电厂.电厂的经济和技术数据如表1所示,取自于国际能源署的MINUIT (Modeling Investmentwith Uncertainty ImpacTs)模型中所给定的数据[11],但做了一些修改.为更清楚地描述发电公司间的博弈行为,假设所研究电力系统具有中等规模,初始装机容量和最大负荷分别为5000和4200MW.

表1 电厂的技术经济数据Table 1 Techno-economic data of power p lants

给定X、Y和Q均为100.在应用B-M方法时,将每个规划子周期内的最大负荷值、燃料价格和CO2排放价格都划分为 2个区块(具体细节见附录).由于燃料价格分为电煤价格和天然气价格,这样每个子周期内将包含JΩ=16个市场状态.之后,计算这些市场状态下不同发电公司所对应的投资收益gt,jΩ,并平均分配到J=8个区块之中.在形成市场状态区块jΩ时,按 (负荷、电煤价格、天然气价格、CO2排放价格)的模式进行,并以其区块编号所组成的二进制编码代表实际的市场状态区块编号,如(0, 0,0,0)代表区块 0,(1,1,1,1)代表区块15.

其它数据如下:

(1)每个规划子周期内的无风险利率r(t)均为10%;

(2)电煤价格 pcoal,0为2500美元/TJ,每个规划子周期内的增长率 μcoal为 2.5%,标准差 σcoal为4.2%;

(3)天然气价格 pgas,0为 5500美元/TJ,每个规划子周期内的增长率 μgas为 1.8%,标准差 σgas为3.6%;

(4)最大负荷在每个规划子周期内的增长率 μL为2.4%,增长率的标准差σL为2%;

(5)CO2初始排放价格 pCO2,0为15美元/t,每个规划子周期内的增长率μCO2为2.5%,标准差σCO2为5.2%,比例因子η为1.假设在第3个规划子周期即 =3时,《京都议定书》第一承诺期结束以后的国际减排安排将达成协议,各协议国的减排配额会重新进行分配,从而导致 CO2排放价格有可能出现跳跃现象.

(6)市场电价上限 ¯pe为150美元/(MW◦h),装机容量价格上限¯pc为210美元/(MW◦d).

采用第 2节的方法,可求得发电投资项目在每个规划子周期内各个区块的投资收益、期权价值以及相应的投资触发点.表 2列出了投资收益区块与市场状态区块的对应关系,表 3则列出了规划周期内各发电公司的投资期权博弈结果.

从表 3可以看出,在市场状态会发生随机变化的情况下,发电公司的投资决策并不是固定不变的,其投资时机将随着市场状态的变化而变化.如在第1个和第 2个规划子周期,3个发电公司都不选择投资.在第 3个规划子周期,当市场状态使得发电公司C的投资收益不低于第2个收益区块值时,发电公司C会率先投资;随后,发电公司A会在第4个规划子周期进行投资,触发其投资的市场状态应使得其投资收益不低于第 3个收益区块值;最后投资的为发电公司B,其将在第5个规划期进行投资.如果在第 3个规划子周期,实际市场状态未达到触发发电公司 C投资的区块,则发电公司 C将会选择等待,以期待更好的投资机会.接下来在第 4个规划子周期,发电公司 C将会判断市场状态是否能使得其投资收益不低于第 3个收益区块值,如果是,则发电公司C又会选择率先投资.

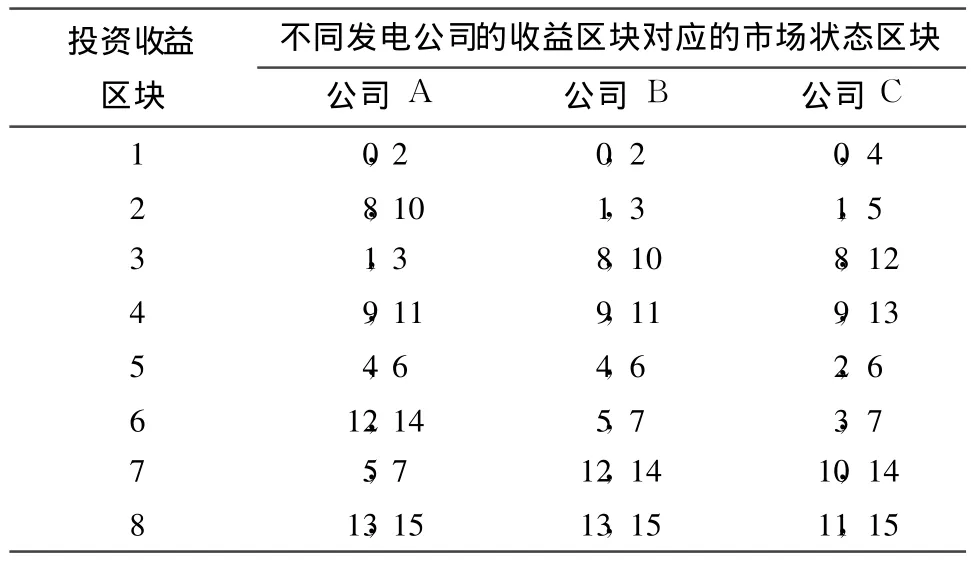
表2 收益和市场状态区块的映射关系Table 2 Mapping relationships between p rofit blocks and market state blocks

表3 发电公司投资期权博弈结果1)Table 3 Resu lts of the options-game among generation companies

在第 5个规划子周期,当市场状态使得发电公司A的投资收益不低于第 1个收益区块值时,即市场状态区块为{0,2}时,发电公司A会率先投资;而当市场状态使得发电公司 C的投资收益不低于第 2个收益区块值时,发电公司 C也会率先投资,此时对应的市场状态为{0,4,1,5}.这样,当市场状态位于区块0时,发电公司A和C同时达到了投资触发点.此时,需要比较这两个公司期望的投资收益回报率,回报率高的会率先投资.经过比较,发电公司 A的投资收益回报率更高些.

由表 3可知,在整个规划期内发电投资顺序是动态变化的,不同的市场状态下会出现不同的率先投资者和追随投资者,从而导致不同的发电投资顺序.这在一定程度上也说明了当存在多个不确定性因素时,发电投资过程本质上是个多方博弈均衡过程,博弈结果会根据不确定性因素的变化而变化.这与发电投资领域的实际情况也是相符的,例如当天然气价格较高而电煤价格较低时,打算投资燃煤电厂的发电公司通常会先进行投资;而当 CO2排放价格较高时,打算投资CCGT电厂或投资带有CCS装置燃煤电厂的发电公司可能就会成为率先投资者.

5 结语

文中综合考虑了电力市场环境下的不确定性和未来限制温室气体排放政策的不确定性对发电投资决策的影响.利用期权博弈理论和B-M实物期权定价方法,发展了发电投资决策新的模型框架,构造了计及发电公司间动态博弈过程的数学模型,发展了求解方法.算例分析结果表明,所发展的模型框架能够合理容纳多个不确定性因素,适当模拟规划期内多个发电公司在市场状态随机变化情况下的动态博弈过程.

附录表1 区块的负荷均值MW

表2 区块的电煤价格均值美元/TJ

表3 区块的天然气价格均值美元/TJ

表4 区块的CO2排放价格均值美元/t

[1] Wu F F,Wen Fu-shuan,Duan Gang.Generation planning and investment under deregulated environment:comparison of USA and China[J]∥Proceedings of IEEE PES 2004General Meeting,2004(2):1324-1328.

[2] Abadie LM,Chamorro JM.European CO2price and carbon capture investments[J].Energy Economics,2008,30 (6):2992-3015.

[3] Lucas R E,Prescott E C.Investment under uncertainty [J].Econometrica,1971,39(5):659-681.

[4] Baldursson F,Karatzas I.Irreversible investment and industry equilibrium[J].Finance and Stochastics,1997, 1(1):69-89.

[5] 安瑛晖,张维.期权博弈理论的方法模型分析与发展[J].管理科学学报,2001,4(1):38-44.

An Ying-hui,ZhangWei.Analysis and development of the method and model of op tion-game theory[J].Journal of Management Sciences in China,2001,4(1):38-44.

[6] 许诺,文福拴,黄民翔.基于期权博弈理论的发电投资决策[J].电力系统自动化,2007,31(14):25-30.

Xu Nuo,Wen Fu-shuan,Huang Min-xiang.An optiongame based approach for generation investment decisionmaking[J].Automation of Electric Power Systems,2007, 31(14):25-30.

[7] 贾德香,程浩忠,韩净.发电投资的期权博弈决策方法[J].电力系统自动化,2007,31(8):17-21.

Jia De-xiang,Cheng Hao-zhong,Han Jing.An approach to generation investment decision-making based on real option game in powermarket environment[J].Automation of Electric Power Systems,2007,31(8):17-21.

[8] 王勇,文福拴,钟志勇,等.基于实物期权理论的发电投资决策和容量充裕性评估 [J].电力系统自动化, 2005,29(19):1-8.

Wang Yong,Wen Fu-shuan,Chung CY,etal.Real option based approach for generation investmentdecision-making and generation capacity adequacy analysis[J].Automation of Electric Power Systems,2005,29(19):1-8.

[9] 刘国中,文福拴,薛禹胜.计及温室气体排放限制政策不确定性的发电投资决策 [J].电力系统自动化, 2009,33(18):17-22.

Liu Guo-zhong,Wen Fu-shuan,Xue Yu-sheng.Generation investment decision-making under uncertain greenhouse gas emissionm itigation policy[J].Automation of Electric Power Systems,2009,33(18):17-22.

[10] 王晛,李渝曾,张少华.求解电力市场均衡模型的非线性互补方法[J].电力系统自动化,2004,28(1):7-11.

Wang Xian,Li Yu-zeng,Zhang Shao-hua.A nonlinear comp lementary approach to the solution of equilibrium models for electricitymarkets[J].Automation of Electric Power Systems,2004,28(1):7-11.

[11] Yang M,Blyth W,Brad ley R,et al.Evaluating the power investment options with uncertainty in climate policy [J].Energy Economics,2008,30(4):1933-1950.