改进灾变遗传算法及其在无功优化中的应用*

蒋金良 林广明 欧阳森 曾江

(华南理工大学电力学院,广东广州 510640)

遗传算法(GA)作为一种强大的全局优化算法,已成功应用于电力系统无功优化[1].但GA存在易早熟、收敛稳定性差以及在遗传后期收敛速度慢等缺陷.为此,文献[2]中在GA的基础上引入了灾变算子,首先提出了灾变遗传算法.文献[3]中介绍了灾变算子的仿生学意义及灾变GA对GA全局性能的改善作用,并对灾变算子作了改进.文献[4]中将灾变GA应用于电网购电计划优化中,文献[5]中则将灾变GA应用于配电网开关优化配置的计算中,均取得了较好的效果.

虽然灾变GA很好地提高了GA的全局性能,但上述文献没有对其稳定性加以考虑,为此,文中在分析灾变算子对遗传算法稳定性影响的基础上,提出了一种改进的灾变遗传算法.算法从GA群体整体进化过程出发,设计了与进化代数相关的灾变规模控制策略,以提高算法后期的稳定性;此外,设计了与进化代数相关的交叉概率和与个体适应度相关的自适应变异概率,以提高算法的收敛性能.将算法应用于电力系统无功优化的经典算例IEEE14和IEEE30节点中,结果证明了改进算法的有效性.

1 改进的灾变遗传算法

1.1 常规灾变算法原理及其步骤介绍

常规灾变GA是在GA的基础上,模拟自然界的灾变现象,当判断连续数代最佳染色体没有任何进化,或者各个染色体已过于近似时,即可对当前种群采取灾变手段.灾变GA的具体步骤为[2]:

(1)染色体初始化,形成初始种群;

(2)计算每一代染色体的适应值;

(3)遗传进化操作,即选择、交叉、变异;

(4)判断群体是否陷入未成熟收敛状态,若是则先保留当前群体中的若干优秀个体,再进行灾变操作,灾变后形成新群体转;否则直接进入下一步;

(5)判断是否收敛或达到迭代次数,若是则输出结果并结束;否则转步骤(2).

1.2 改进灾变算子的设计

1.2.1 灾变算子对GA收敛性能的影响.

由上节可知,常规灾变 GA通过在算法后期强行打破群体高度同化的状态,使新产生的群体进入下一阶段的遗传进化中,从而有效提高算法的全局性能.然而,常规灾变GA忽略了灾变算子(包括灾变算子和灾变手段)对收敛性能的影响.为此,这里对常规灾变算子和GA收敛性能的关系进行深入分析.

1)常规灾变条件对 GA收敛性能的影响

目前提出的灾变条件大多是基于对早熟收敛的判断或引入尖点灾变模型进行判断[2,5],这些方法存在如下缺陷:

(1)会使得在计算后期种群收敛时算法仍引入灾变,导致算法后期的收敛稳定性变差,甚至导致不收敛.

(2)上述条件可能导致灾变过于频繁,增加搜索的盲目性,使收敛速度减慢.

可见,常规灾变 GA的缺陷主要在于没有考虑算法后期的收敛性问题.

2)常规灾变手段对GA收敛性能的影响.

传统的灾变手段有很多,典型的灾变手段有[2-3]:①突然增大变异率;②保留最好解,重新初始化其他的个体;③对不同的个体实施不同规模的变异.

上述灾变手段对算法的收敛性具有很大的影响:

(1)产生的新个体随机散落在整个解空间中,增加了搜索的随机性.

(2)新群体中充斥着许多劣质个体,这些个体在新阶段的交叉操作中可能破坏原先得到的优秀个体,致使算法收敛过程加长.

(3)整体进化过程中灾变程度保持不变,可能破坏算法的后期稳定性.

综上所述,由于常规灾变算子只截取了进化过程中的某一断面进行设计,忽略了种群整体进化过程中的连续性,因而算法的可控性较差,影响其收敛性;且灾变手段的设计具有很大的随机性和盲目性,致使算法的搜索效率不高.文中认为灾变算子的设计应该从群体的整体进化过程出发,综合考虑算法的搜索性,收敛性和稳定性.

1.2.2 灾变过程的收敛性控制

从种群进化的整体过程来看,初期应尽可能对整个解空间进行搜索,避免过早陷入局部最优解,此时群体的平均适应度值的变化幅度较大;随着进化的进行,种群开始稳定收敛,此时种群中的个体向某一最优解集中,群体平均适应度值逐渐趋于某一稳定值.因此,为了保证算法的收敛性和稳定性,灾变的程度应该随着进化代数逐渐减弱,由于灾变的规模大小(灾变时新生成的个体数量,记为Nc)体现了灾变程度的强弱,为此,文中提出通过控制进化过程中灾变规模大小来控制灾变的程度,并设计与进化代数相关的自适应灾变规模控制策略如下:

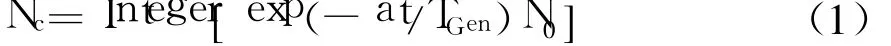
式中:Integer[]是指对参数取整;a为灾变规模曲线参数;TGen为最大进化代数;t为当前进化代数(0≤t≤TGen);N0为预设灾变数量.

灾变算子的具体设计如下:

(1)灾变条件:若当前进化代数为预设的灾变间隔代数的整数倍,则实施灾变.

(2)灾变操作具体步骤:①保留当前种群的最优解.②利用公式(1)随机生成Nc个个体.③用随机生成的Nc个个体替换当前种群中Nc个最差的个体.

以上设计具有以下优点:

(1)兼顾搜索性、收敛性和稳定性 Nc在进化初期接近于 N0,并随着进化代数逐渐减小,有利于加强算法初期的搜索性和保护算法后期的收敛性和稳定性.

(2)可控性强 只需选取适当的灾变规模曲线参数a,即可实现对灾变程度的自适应控制.

(3)实现简单 灾变手段为初始化群体,易于编程实现.

(4)计算量小 灾变规模随着进化代数逐渐较小,减小了新个体目标函数值的计算量.

1.3 自适应交叉概率和变异概率的设计

1.3.1 自适应交叉概率的设计

已有的研究成果表明[6-7],固定的交叉概率会影响GA初期的搜索性能和末期的收敛性能.为此,文献[7]中设计了与进化代数相关的交叉概率.

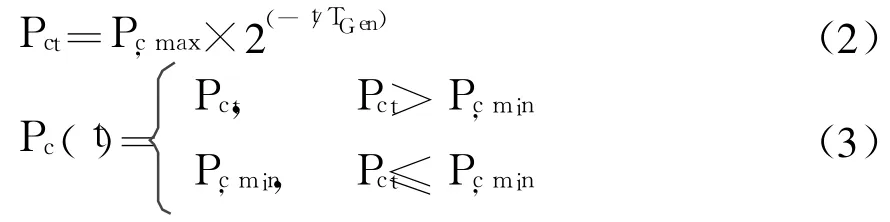
式中:Pct为一个中间计算变量;TGen为预设的最大进化代数;t为当前进化代数(0≤t≤TGen);Pc,max为预设置的最大交叉概率;Pc,min为预设置的最小交叉概率;Pc(t)为当前种群(第t代)的交叉概率.

在此基础上,文中提出了利用sigmoid函数设计的与进化代数相关的交叉概率计算公式[8]:

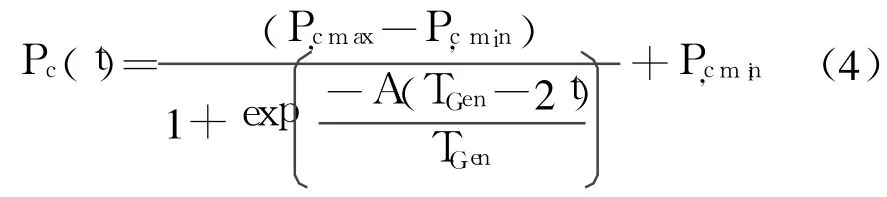
式中:A=9.903438.

该公式所对应的自适应调整曲线在算法的初期和后期都近似于直线,这有利于加强算法在初期对新个体的开发和在后期保护算法的稳定性.

1.3.2 自适应变异概率的设计

变异可以产生新的模式,提高搜索的范围.从种群的个体进化角度来看,同一代种群中各个个体的变异概率应该随个体的优劣而变化.此外,为了保证算法的稳定性,变异概率的总趋势应该是能逐渐减小而使群体能够迅速集中.由此给出自适应变异概率如下:

式中:Pm,max为预设置的最大变异概率;Pc,min为预设置的最小变异概率;Pm(t)为第t代种群中个体Xi的变异概率;A=9.903438;f(Xi)为待变异个体的适应度值;fmax为第t代群体中的最优个体适应度值.

2 改进灾变遗传算法的性能分析

2.1 测试函数

为验证改进灾变遗传算法(ICGA)的性能,文中选取以下测试函数:

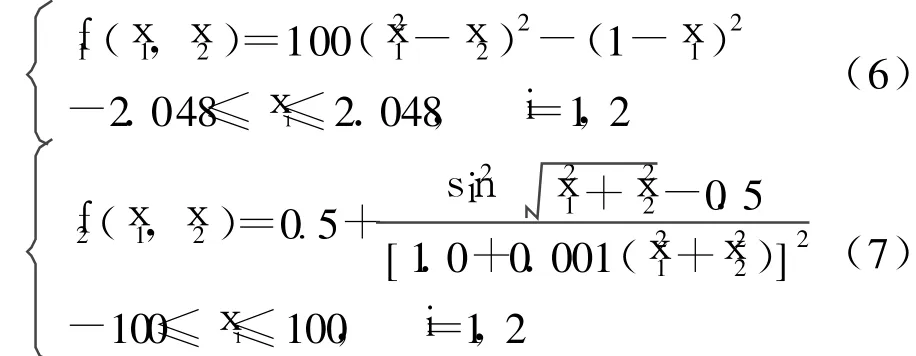
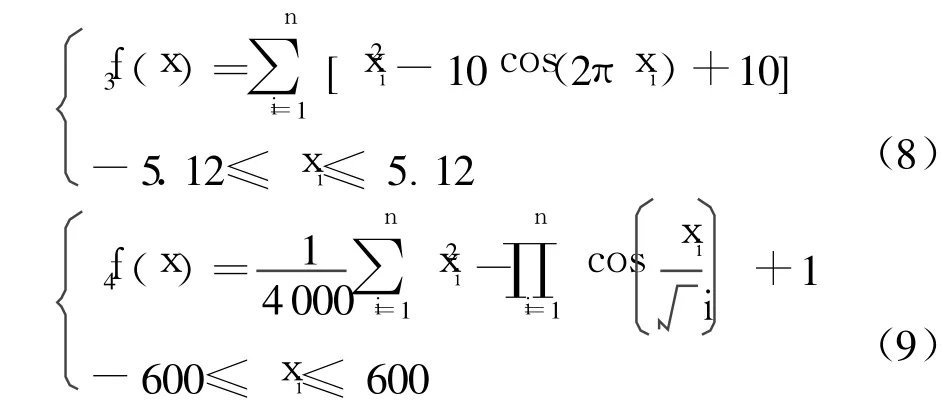
式中:函数f1、f2为典型的二维GA测试函数;f1为病态的连续单峰值函数,全局极小值点为 f1(1, 1)=0;f2有无数个局部极小点,全局极小值点为f2(0,0)=0;f3、f4为多峰测试函数,全局极小值点为f2(0,0,…,0)=0.

2.2 算法性能

利用简单遗传算法(SGA),文献[9]中的自适应遗传算法(AGA)和ICGA对上述测试函数分别进行 100次优化计算,求其全局最小值,计算结果如表1所示.经过多次仿真实验,给出各算法参数为:对函数f1和f2,群体数为60,TGen=100,N0=59,n= 10;对函数 f3和 f4,群体数为 350,TGen=700,N0= 349(此外,对f1～f4,SGA中Pc=0.9,Pm=0.1;AGA中k1=k3=1,k2=k4=0.5;ICGA中Pc,max=0.9, Pc,min=0.5,Pm,max=0.1,Pm,min=0.01,a=10).收敛条件综合考虑最大进化代数、最小目标函数值和平均目标函数值在连续 4～6代的变化来决定算法结束.

表1 SGA、AGA和ICGA性能比较Table 1 Comparison of performance of SGA,AGA and ICGA

由表1可知,ICGA在收敛速度、收敛稳定性和收敛精度上均明显优于SGA和AGA,很好地兼顾了全局性能和局部搜索能力,对于多峰值函数 f2～f4, ICGA具有很高的收敛成功率,这说明ICGA具有很强的摆脱局部极值的能力.

3 无功优化数学模型

3.1 目标函数

文中以电压合格率最高、系统有功网损最小为目标函数,把负荷节点电压越限和 PV节点的发电机无功越限这两类不等式约束作为罚函数,从而构成电力系统无功优化的模型如下式所示[10]:

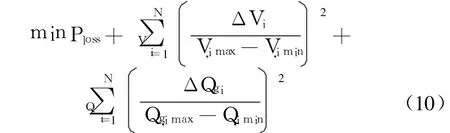
式中:

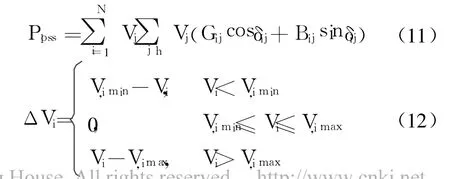
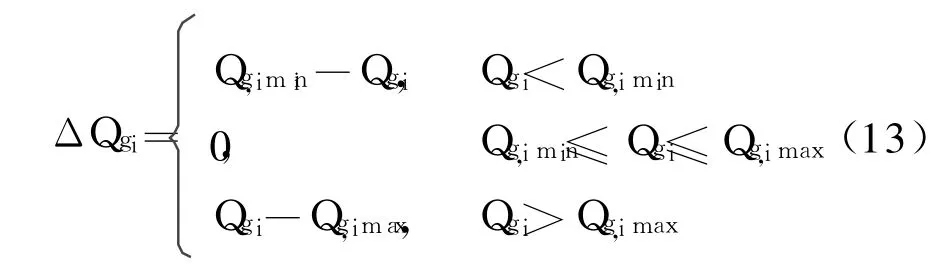
式中:Ploss为系统有功损耗;V、Q分别为电压越界和无功越界罚系数;Vi、Vi,min、Vi,max分别为节点电压、电压下限及上限;Qgi、Qgi,min、Qgi,max分别为发电机无功出力、无功出力下限及上限;Gij、Bij、δij分别为节点i、j之间的电导、电纳和相角差;N为节点总数;目标函数中第 1项为网损,第 2项为电压越界罚函数,第3项为无功越界罚函数.

3.2 变量约束方程

文中在优化中选取了无功补偿器容量Qc,可调变压器的变比 T和发电机机端电压作为控制变量Vg,以PQ节点电压和发电机节点无功出力为状态变量,控制变量约束为

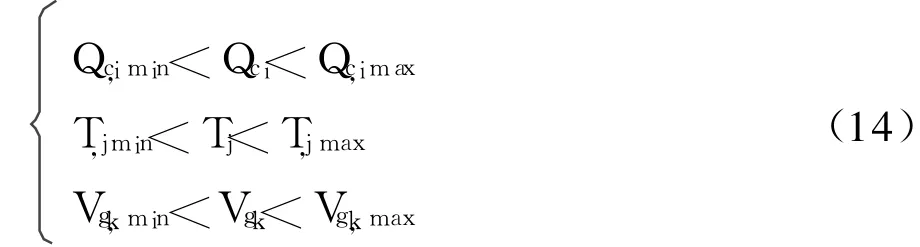
式中:Ci,max、Ci,min分别为并联补偿电容量的上、下限;Tj,max、Tj,min分别为变压器变比的上、下限;Vgk,max、Vgk,min分别为发电机机端电压的上、下限;i、j、k分别在系统中无功补偿点数,变压器台数和发电机台数范围内取值,状态变量约束为

4 无功优化计算结果与分析

4.1 IEEE14节点测试系统

IEEE14节点系统是典型的电力系统拓扑之一[11],文中分别采用ICGA、SGA和文献[2]中的灾变遗传算法(CGA)对该系统进行无功优化.设定改进灾变遗传算法基本参数为:群体数为 30,最大预设进化代数TGen=30,N0=29,V=1.5,Q=1.5.表2给出了IEEE14节点系统各变量的约束范围、初始状态及其各种方法的优化结果.

由表 2可知,初始状态中,负荷节点电压 UD3～UD14均低于下限,发电机节点无功 QG2越上限.3种方法的优化结果均消除了以上越限,经过ICGA优化后,各节点电压在更高的水平上运行,找到的最优解有更小的网损值,全局寻优能力更强.

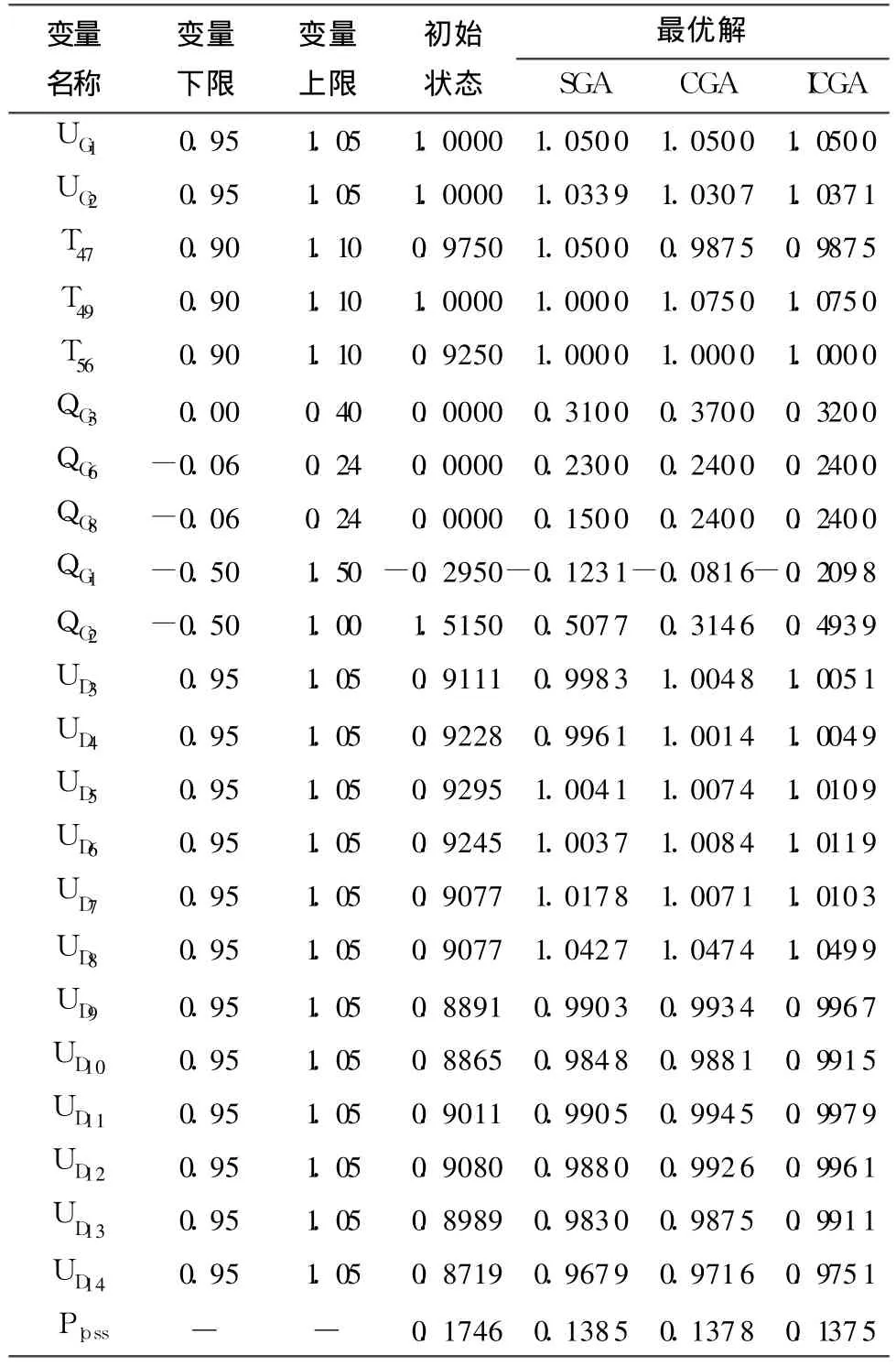
表2 IEEE14节点系统优化结果Table 2 Op tim ization results of IEEE 14-bus system

表3为 30次计算后的有功网损的统计值,由表3可知,ICGA的最小值与平均值最为接近,且标准差很小,说明ICGA具有良好的收敛稳定性.

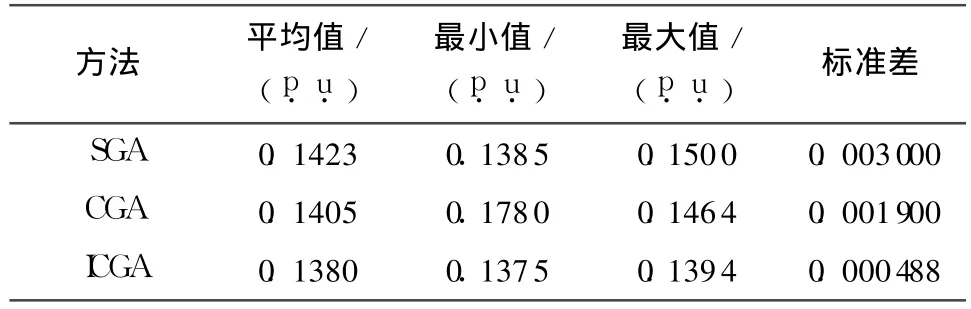
表3 统计 30次优化后网损值的计算结果Table 3 Statistical optim ization results of network loss by 30 times calculation

4.2 IEEE30节点测试系统

IEEE30节点测试系统的支路数据及接线图见文献[12],初始有功网损为0.059879(p.u.),且有3个节点的电压越下限,即V26=0.932(p.u.),V29= 0.940(p.u.),V30=0.928(p.u.).

将ICGA对测试系统进行优化后的结果与SGA,AGA[12],以及改进量子遗传算法(IQGA)[10],自适应粒子群算法(APSO)的优化结果进行比较[13],如表 4所示.

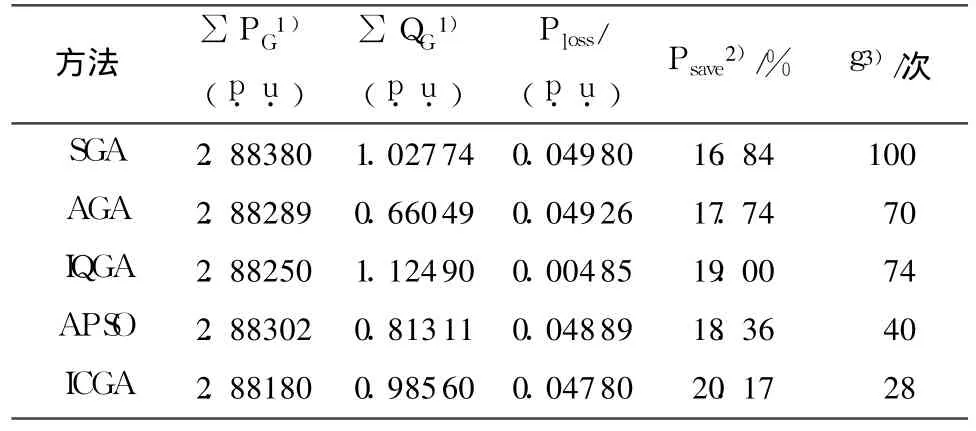
表4 不同方法的优化比较结果Table 4 Optim ization com parison resu lts of differentmethods

由表4可知:(1)采用文中的方法得到的Ploss为0.0478(p.u.),Psave为20.17%,优化效果最好;(2) ICGA的计算精度明显优于另外4种算法;(3)ICGA的收敛性好,在第 28次迭代时就找到了最优解,收敛速度大大优于其它算法.

5 结语

文中从遗传算法的稳定性和可控性入手,对灾变遗传算法进行改进,建立了改进灾变遗传算法模型,设计了与进化代数相关的交叉概率和与个体适应度相关的自适应变异概率.GA测试函数计算结果表明,该改进算法的稳定性较好,且算法的收敛性能和收敛速度都有了极大的提高.IEEE14和IEEE30节点算例表明,该算法可有效应用于电力系统的无功优化中.

[1] Yan Hong-wen,Tao Jun-na.Reactive power optimization research of power system considered the generation transmission and distribution[C]∥Proc of IEEE International Conference on Industrial Technology.Chengdu:[s. n.],2008:1-4.

[2] 金希东,李治.遗传 -灾变算法及其在非线性控制系统中的应用[J].系统仿真学报,1997,9(2):111-115.

Jin Xi-dong,Li Zhi.Genetic-catastrophic algorithms and its application in non linear control system[J].Proceedings of System Simulation,1997,9(2):111-115.

[3] 张勇军,任震,钟红梅.基于灾变遗传算法的无功规划优化[J].电力系统自动化,2002,26(23):29-32.

Zhang Yong-jun,Ren Zhen,Zhong Hong-mei.Cataclysmic genetic algorithms based op timal reactive power planning [J].Automation of Electric Power Systems,2002,26 (23):29-32.

[4] Zhang Yong-jun,Yuan Wen-gen,Li Bang-feng,etal.Optimal power purchase p lanning of hainan power grid company[C]∥The 8th International Power Engineering Conference.Singapore:[s.n.],2007:1854-1858.

[5] 王东,史燕琨,丛吉远,等.灾变遗传算法在配电网开关优化配置中的应用[J].高压电器,2004,40(3): 180-182.

Wang Dong,Shi Yan-kun,Cong Ji-yuan,et al.Application of catastrophic genetic algorithm to the optimal configuration of switching devices in distribution system[J].H igh Voltage Apparatus,2004,40(3):180-182.

[6] 廖美英,张勇军.灾变算子在遗传算法中的作用研究[J].计算机工程与应用,2005,41(13):54-56.

Liao Mei-ying,Zhang Yong-jun.Study on the effect of cataclysm operator on genetic algorithm[J].Computer Engineering and Application,2005,41(13):54-56.

[7] 欧阳森,王建华,宋政湘,等.一种新的改进遗传算法及其应用 [J].系统仿真学报,2003,15(8):1 066-1073.

Ouyang Sen,Wang Jian-hua,Song Zheng-xiang,et al.A new imp roved genetic algorithm and its application[J]. Proceedings of System Simulation,2003,15(8): 1066-1073.

[8] Mennon A,Mehrotra K,Mohan CK,etal.Characterization of a class of sigmoid functionswith app lications to neural networks[J].Neural Networks,1996,9(5):819-835.

[9] Srinivas M,Patnaik LM.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Trans on SystemsMan and Cybernetics,1994,24(4):656-667.

[10] 刘红文,张葛祥.基于改进量子遗传算法的电力系统无功优化[J].电网技术,2008,32(12):35-38.

Liu Hong-wen,Zhang Ge-xiang.A reactive power optim ization method based on improved quantum-inspired genetic algorithm[J].Power System Technology,2008,32 (12):35-38.

[11] 张勇军.电力系统无功优化的灾变遗传算法及MAS模型研究[D].广州:华南理工大学电力学院,2004.

[12] Wu Q H,Cao Y J.Optimal reactive power dispatch using an adaptive genetic algorithm[J].Electrical Power＆Energy Systems,1998,20(8):563-569.

[13] 李丹,高立群,刘佳,等.基于APSO算法的电力系统无功优化[J].计算机工程,2008,34(23):17-19. Li Dan,Gao Li-qun,Liu Jia,et,al.Power system reactive power optimization based on adaptive particle swarm optimization algorithm[J].Computer Engineering,2008, 34(23):17-19.