城市公交网络的鲁棒性分析模型*

段后利 李志恒 张毅

(清华大学自动化系,北京 100084)

城市公交系统是与城市交通系统和社会经济环境相联系的、复杂的、开放的大系统.如何更好地改善城市公交系统的性能,为更多的旅客提供更好的服务,是交通学者和工程师一直在探索的目标.其中,公交网络拓扑结构的鲁棒性是考核城市公交网络性能的重要指标,尤其是在路网发生拥堵或者是交通事故的情况下,公交网络的鲁棒性很大程度上决定了公交系统的整体性能.

国内外学者的研究已经证实了城市公交网络的复杂网络特性[1],因此,对其分析也可以归类为复杂网络的特性分析.复杂网络的鲁棒性分析一直是国内外学者研究的热点.Albert等[2]比较了随机网络和无尺度网络(一种典型的复杂网络)的连通性,指出这两种网络对于随机故障和蓄意攻击的鲁棒性存在着显著的差异.Cohen等[3-4]运用渗流理论,分析得到了在随机攻击和蓄意攻击情况下Internet网络的鲁棒性.Bollobas等[5]则运用随机图理论对复杂网络的鲁棒性和脆弱性作了数学分析.何胜学等[6]通过研究公交线网的生成机理,分析了公交线网在随机节点删除和蓄意节点删除下的鲁棒性.

上述研究在复杂网络鲁棒性分析领域均取得了重要的成果,但其分析均只针对复杂网络的原始拓扑模型.对于公交系统而言,基于底层路网结构的原始公交网络拓扑模型仅可以表现站点之间的地理位置关系及其在底层路网上的连通关系,而不足以表现公交线路和公交站点之间的关系.为此,文中引入了二分图模型,用以对城市公交系统进行建模,并在此网络模型基础上进行系统鲁棒性分析.二分图是图论里面的一种在理论研究和实际应用中都有重要意义的特殊模型.在二分图中,所有顶点被分成两个集合M和N,其中M或N中任意两个在同一集合中的点都不直接相连,但M中的节点两两之间通过N中的节点发生联系,同样 N中的节点两两之间通过M中的节点发生关系.基于该模型,可以对应地建立公交站点和线路之间的关系,从而从不同的角度建立公交网络的拓扑模型.

文中以北京市公交系统为例,将其表示成二分图模型,并从该模型出发分别构建了公交原始网络模型、公交站点网络模型和公交线路网络模型.随后定义了城市公交路网的鲁棒性指标,并设计了新型的鲁棒性分析快速算法.最后,基于北京市公交网络的实际数据,分析上述 3种网络模型在随机攻击、按度数的分布攻击和按介数攻击 3种情况下的鲁棒性.

1 公交系统网络模型

1.1 原始公交网络及其二分图模型

原始公交网络是由公交停靠站点和站点间的路段组成的网络,如图1(a)所示.一条公交线路要经过若干停靠站点,同时一个停靠站点会有若干公交线路经过.线路与线路之间通过交汇的停靠站点发生联系,站点与站点之间通过公交线路相联系.因此,公交网络可通过二分图来表示.

公交系统的二分图模型是一个包括两个顶点集合的网络,分别包括公交线路集合 M和公交站点集合 N,如果某条公交线路经过某些站点,则将那些站点与该公交线路用一条无向直线相连接.图1(b)所示是两条具有交汇站点的公交线路的二分图模型,其中顶层节点集合(A;B)为公交线路节点集合,底层节点集合(A1,A2,…,A7;B1,B2,…,B7)是公交站点节点集合.可见二分图模型反映了公交站点和公交线路的包含和被包含关系.

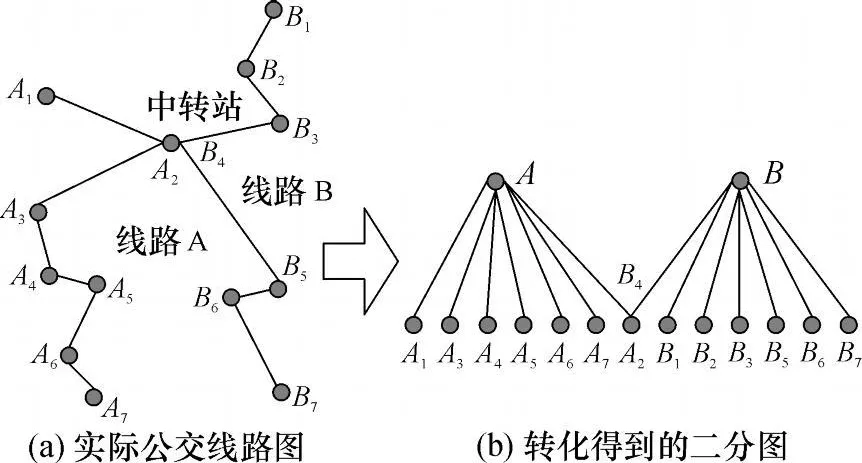
图1 公交系统的二分图模型Fig.1 Original transit network and corresponding bipartite graph models

1.2 公交站点网络与公交线路网络

由公交二分图可以分别构建公交站点网络和公交线路网络.公交站点网络以公交站点为节点,如果存在连接两个站点的一条或多条公交线路,则这两个站点之间存在唯一的连接(边),边的权重等于两站点间的公交线路数,如图2(c)所示;公交线路网络是以公交线路为节点,若两线路之间存在一个或多个共同站点,则这两条线路间存在唯一的连接(边),边的权重等于共同站点数,如图2(b)所示.

公交站点网络用来考察公交站点与站点之间的连通性,这种连通性不是考察公交站点之间的几何距离,而是考察站点与站点之间的换乘次数.公交线路网络,则主要关注线路与线路之间的共同站点数,以及公交线路之间换乘的难易.

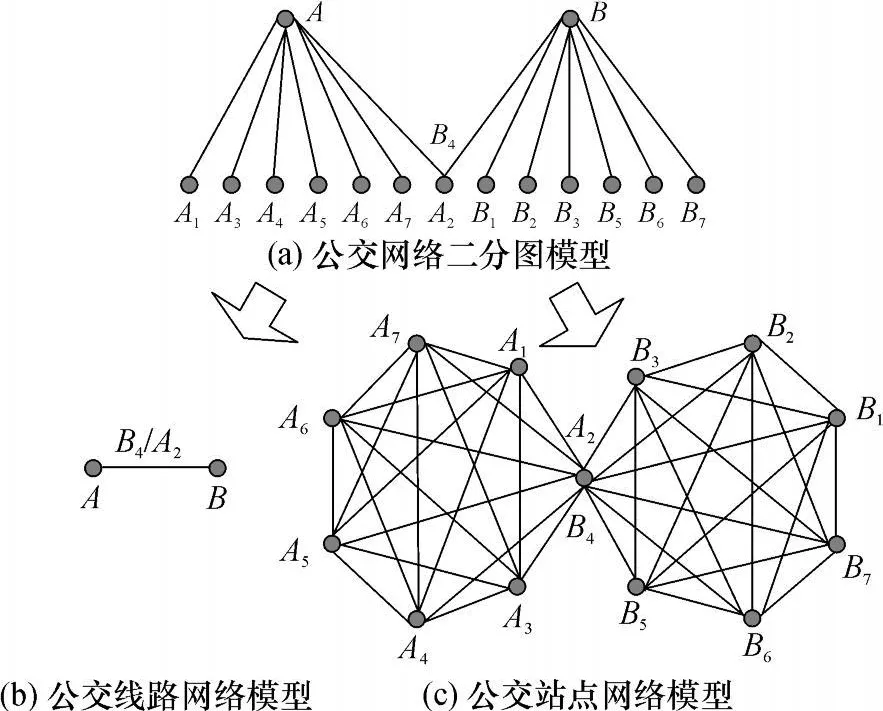
图2 公交站点网络与公交线路网络模型Fig.2 Transit stations network and transit lines network

文中将以北京市公交系统为例,应用文中提出的网络模型对其进行鲁棒性分析.北京市公交公司2003年一共拥有 417条公交线路,其中夜班线路 10条,日间线路 407条,由于夜间车与日间车运行的时段不同,有必要将夜间车与日间车区别开来,故在此预先删去夜间班车线路.这 407条日间班车线路共经过3095个不同的站点.

我们先将其表示成由 407个公交线路节点和3095个公交站点节点构成的二分图,然后如图 2所示转化为相对应的公交线路网络和公交站点网络.图 3中取北京市二环以内的5条公交线路和 50个公交站点为例,将其用二分图表示,再分别构建出公交线路网络和公交站点网络.图3(a)是原始公交网络图,图3(b)是其二分图模型,图3(c)、(d)分别是通过二分图构建出的公交站点网络和公交线路网络.

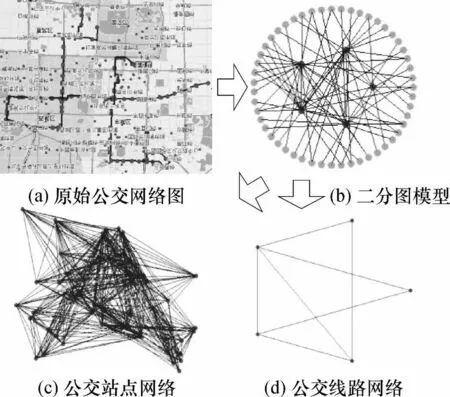
图3 北京市公交系统网络建模示例Fig.3 Demonstration ofmodeling the transitnetwork of Beijing

2 城市公交网络的鲁棒性定义

2.1 公交网络的鲁棒性指标定义

通常一个图中任意两个节点 i,j之间存在着一定的路径,在这所有的路径中最短的路径称为节点i,j之间的最短路径 dij.一个图的平均路径长度(APL)l定义为所有的节点i,j之间的最短路径的平均值.即:

式中:n为图中节点的数量.

文中统一选用APL这一参数来分析路网在各种模型中的鲁棒性.在公交原始网络中,平均路径长度与公交车运行速度的比值对应着乘客的平均旅行时间;在公交站点网络中,平均路径长度对应于从任意两站点之间所需的平均换乘次数;在公交线路网络中,平均路径长度对应着两线路之间的平均换乘次数,也体现了线网整体的运行效率.

综上所述,在公交网络的鲁棒性分析中,以网络平均路径长度作为其中一个衡量指标是合理的.Albert等[8]在研究Internet网络鲁棒性时发现,随着去点率 fc的加大,平均最短路径先变大后变小.因此,他们定义引起网络的平均路径长度达到峰值时的去点率fc为鲁棒性指标0,该指标被证明是实用且有效的.因此,文中定义公交网络中的鲁棒性指标为使得网络平均路径长度 l达到最大时的去点率fc,

该鲁棒性指标fc越大,说明网络的鲁棒性越好.

2.2 对公交网络的攻击方式分析

对交通网络的“攻击”,指的是引起公交网络节点或者边发生故障,从而导致交通网络效率产生明显下降的事件或行为.攻击可以分为随机性攻击和选择性攻击.对公交网络的攻击主要包括以下几种情况.

(1)实际公交系统中公交线路运行时段不一致.

实际公交系统中,由于各种原因,线路运行的时段并不是一致的.这样就造成了在公交线路网络中,在某一特定的时段,某些公交线路由于停止运行而从网络中消失.这种情况,将会导致公交线路网络中的某些节点被删去,因而可以视为对公交网络的一种“选择性攻击”.

(2)实际公交系统中公交区间车的存在.

区间车是北京市公交系统的一个特点.所谓区间车是指某些公交线路在特定的时段只在原线路的某个区间内运行,也就是只经过原线路的某些站点.对于那些未被经过的站点,反映到公交站点网络中就是这些站点被删去,从而导致公交站点网络的结构发生变化,也就使得网络中的平均路径长度发生了变化,因而可以视为对公交网络的一种“选择性攻击”.

(3)交通事故或道路严重拥堵的发生.

交通事故或者是道路严重拥堵将导致一段时间内事故点(拥堵点)附近的站点因无法通行而从网络中消失,引起经过该站点的线路不通,从而导致该线路余下的所有站点均不可达.这种情况,会导致原始公交网络、公交站点网络、公交线路网络的鲁棒性指标均发生变化,可以视为一种“随机性攻击”.

2.3 基于公交网络特性的鲁棒性分析

真实世界中的网络,一般可以分为随机网络、复杂网络或者规则网络.其中,复杂网络具有“小世界”和“无尺度”的性质[8].规则网络中各个节点的度相同;随机网络节点度的分布服从二项分布,当节点数目足够大时近似于泊松分布;复杂网络度的分布服从幂律分布(Power Law),即节点具有度数k的概率为Pk=Ck-γ,其中,Pk为节点度数为k的概率, C为常数,γ为大于 1的幂律系数[2].

通过对国内外多个城市的公交网络进行研究发现,城市的公交网络都具有“无尺度”网络的性质[6,9].因此,按照对无尺度网络鲁棒性分析的成果,公交网络对随机性攻击应具有很强的抵抗能力,即使 5%的节点失效,网络平均路径长度变化也不大;而对于选择性攻击,尤其是对网络中节点按度数大小排列进行的攻击非常脆弱.这是由于幂律分布决定了大部分的节点度数是很小的,这些节点失效对网络的平均路径长度影响很小;而少数度数很大的节点决定了网络的结构,对于网络的鲁棒性具有至关重要的影响.

3 公交网络的鲁棒性分析算法设计

对于一个具有n个节点,e条边的网络而言,计算其所有节点对之间的最短路径一般是使用Floyd算法,其时间复杂度为O(n3).但Floyd算法的一个缺点是只能每次都计算网络中所有节点对之间的最短路径.如果每删去一个节点后都重新调用Floyd算法来计算所有节点对之间的最短路径,效率将非常低,尤其当网络规模比较大时非常耗时.因此有必要寻找合适的数据结构和算法来提高计算效率.

对于网络G(n,e),设有节点k(k n),且经过k的最短路径有n对节点,分别为(i1,j1),(i2,j2),…, (in,jn).则对于删去k后的网络G′(n′,e′),其所有节点对间的最短路径仅有(i1,j1),(i2,j2),…,(in, jn)发生变化,其余不变.

因此,在设计公交网络鲁棒性分析算法时可以每次只重新计算发生变化了的最短路径,也就是最短路径经过被删除节点的那一部分.算法的描述如下.

设网络G(n,e)的连接关系由邻接表T表示,其节点对间的最短路径长度由距离矩阵 D表示.

(1)用Floyd算法计算出网络G(n,e)的所有节点对之间的最短路径,得到距离矩阵D.

(2)假设删去节点k,然后

(a)在邻接表T中修改节点k连接关系;

(b)距离矩阵D中分别删去第k行和第k列;

(c)搜索整个网络,计算节点k到网络所有其它节点i,j的最短距离,记为d(i,k),d(j,k);

(d)判断,如果节点(i,j)之间的最短距离d(i, j)等于d(i,k)+d(k,j),则认为(i,j)之间存在经过k的最短路径;

(e)找出所有符合条件(c)的节点对(i,j),并按i的大小依次将(i,j)存储在数组中.

(3)依次从数组中读取节点i,如遇 i重复则跳过.使用Dijstra算法计算从i到其余各节点的最短距离.并且将这新的最短距离覆盖未删去节点k之前(i,j)的最短距离.

可以看到,该算法的步骤(3)使用了Dijstra算法而非传统的广度优先搜索算法来计算节点间的最短距离.这是因为广度优先搜索算法的平均时间复杂度为O(n2),但其只能计算单源点到单源点之间的最短路径.虽然Dijstra算法的时间复杂度与广度优先搜索算法相同,但是其优势在于可以一次计算从某单源点到其余各节点的最短路径.而在实际计算中,对于网络G(n,e),删去节点k之后,需要重新计算最短路径的节点对中恰恰有许多是从某个单源点到其余部分节点的节点对.

同时发现,采用邻接表与二叉堆的数据结构来表示网络时,可以将Dijstra算法的时间复杂度从O (n2)降到O(mlgn),但空间复杂度相对要增加些.其中,n为节点数目,m为网络边的数目.而对于大规模网络的鲁棒性分析而言,对时间复杂度的要求更高,因此有必要采用时间复杂度更低的基于邻接表与二叉堆的Dijstra算法.

该算法的复杂度分析如下:在第(2)步寻找经过节点 k的最短路径处,将会用到两个循环,其时间复杂度为O(n2).在第(3)步读入数组平均需要n次循环,其时间复杂度为O(n).在第(3)步通过Dijstra算法计算从i到其余各节点的最短距离的时间复杂度也为O(m lgn).因此删去1个节点后计算所有节点对之间的最短路径长度,其总的时间复杂度为O(n2+nm lgn).而用Floyd算法计算的时间复杂度为O(n3),可见该算法的确能够在一定程度上提高效率.而且该算法对于计算稀疏网络的效果更明显,甚至可以将时间复杂度降低到O(n2+nlgn).

4 案例分析

本节在第 3节介绍的鲁棒性算法的基础上,采用第 2节介绍的平均路径长度变化的峰值来衡量网络的鲁棒性,对北京市公交系统的 3种网络模型的鲁棒性进行分析.

4.1 公交原始网络模型的鲁棒性分析

本节研究了公交原始网络模型的鲁棒性.这里考察了 3种攻击方式下网络的鲁棒性,分别是:①对网络中节点的随机攻击;②对网络中节点按度数大小排列进行的攻击;③对网络中节点按介数大小排列进行的攻击.

在这里采取的随机攻击方式是每步随机地删去一个节点,从而考察网络的平均路径长度的变化情况;而按度数(介数)的攻击方式是每步删去网络中度数(介数)最大的一个节点,从而考察网络的平均路径长度的变化情况.

图4和 5分别给出了公交原始网络和相同规模的随机网络对于 3种攻击方式(随机攻击、按度数攻击、按介数攻击)的平均路径长度的变化情况,考察的指标采用了Albert等定义的引起网络平均路径长度变化达到峰值的去点率 fc的大小[8].从图 4中可以发现,公交原始网络对于按度数攻击的去点率fc约为 0.1,此时其平均路径长度从原来的 11.58上升到 45左右.而随机攻击方式与网络的平均路径长度变化相比按度数攻击方式的影响不大,其峰值去点率fc为0.4,平均路径长度的峰值为 18左右.对于按介数的攻击方式,其峰值去点率fc也为0.1,但引起的平均路径长度变化没有按度数的攻击方式大,其峰值约为 32.这说明公交原始网络对于按度数的攻击方式引起的平均路径长度变化最厉害,其鲁棒性最差.

从图 5也可以看出相同规模的随机网络对于 3种攻击方式的平均路径长度变化情况.对比图4及5可以看出,公交原始网络与随机网络相比,对于随机攻击方式的鲁棒性差别不大,但是对于按度数和按介数的攻击方式的鲁棒性要差于随机网络.

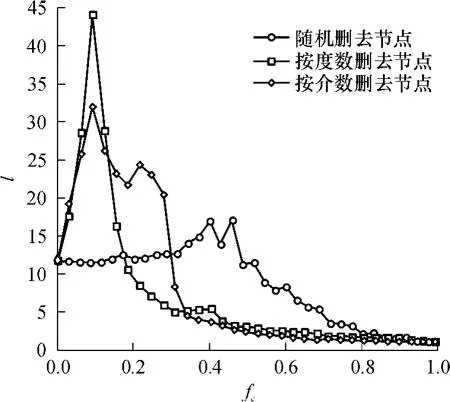
图4 公交原始网络的鲁棒性分析结果Fig.4 Robustness of original transit network

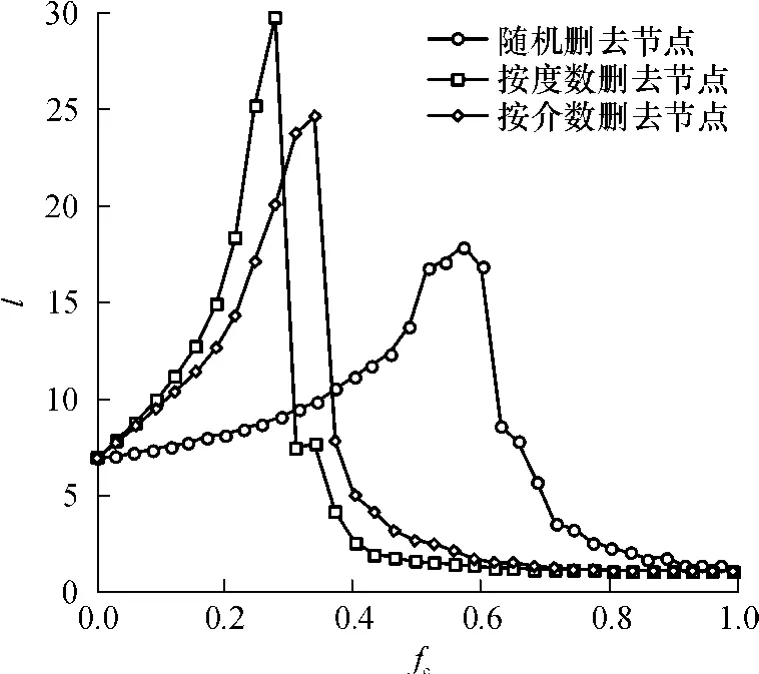
图5 同规模的公交原始随机网络鲁棒性分析结果Fig.5 Robustness of random network comparing with original transit network

4.2 公交线路网络模型的鲁棒性分析

本节研究了以公交线路为节点,线路之间共同的公交站点为连线的公交线路网络的鲁棒性.

图6给出了公交线路网络的平均路径长度随删去节点数变化而变化的情况.注意到网络对于随机地删去节点并不敏感,对于按度数大小来删去节点要相对敏感一些,而按介数大小来删节点介于前两者之间.公交线路网络对于随机攻击引起平均路径长度突变的去点率fc在0.9左右,而对于选择性攻击引起平均路径长度突变的去点率fc在0.75左右.

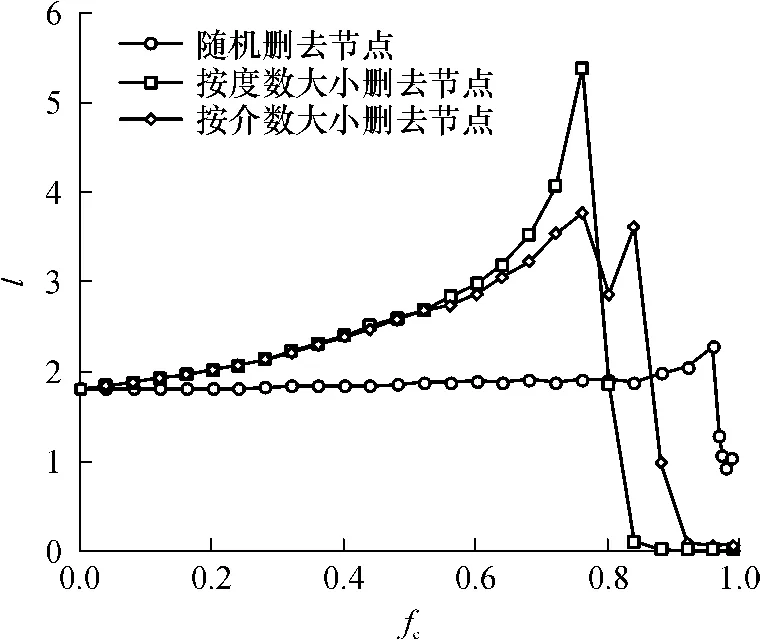
图6 公交线路网络的鲁棒性分析结果Fig.6 Robustness of transit lines network

同时还对相同规模的随机网络的鲁棒性进行考察,并与公交线路网络进行比较.图 7给出了随机网络对于随机攻击、按度数攻击、按介数攻击 3种攻击方式的平均路径长度的变化情况.

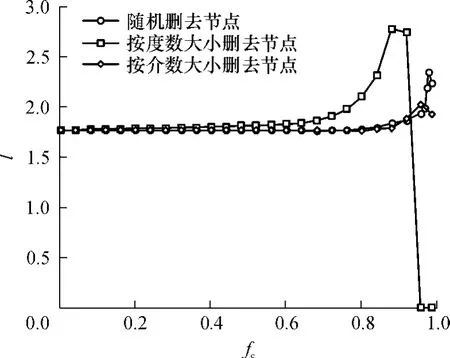
图7 同规模的公交线路随机网络鲁棒性分析结果Fig.7 Robustness of random network comparing with transit lines network

由图7可以看出,随机网络对于随机攻击,其fc也在0.95左右.对于选择性攻击,按介数删节点引起平均路径的变化与随机攻击相似;而对于按度数删节点的攻击方式,fc在0.9左右,可见随机网络对于按度数删节点的鲁棒性要相对差一些.

对比图 6和 7可以发现,公交线路网络和随机网络对于随机攻击都具有较好的鲁棒性,且平均路径长度随去点率增大的变化趋势也基本一致;对于按度数删去节点,随机网络表现出比公交线路更强的鲁棒性.对于公交线路网络,其平均路径长度达到峰值时在 6左右,而随机网络平均路径长度的峰值在 3左右;对于按介数删去节点,随机网络表现出比公交线路更强的鲁棒性.对于公交线路网络其达到平均路径长度峰值在 4左右,而随机网络平均路径长度的峰值在2左右.

4.3 公交站点网络模型的鲁棒性分析

本节研究了以公交站点为节点,站点之间共同的公交线路为连线的公交站点网络的鲁棒性.在这里,也采取3种攻击方式来考察网络的鲁棒性.

图8给出了公交站点网络的平均路径长度随删去节点数变化而变化的情况.注意到网络对于随机地删去节点和按介数大小删去节点并不敏感,而对于按度数大小来删去节点却十分敏感.公交站点网络对于随机攻击和按介数攻击引起平均路径长度突变的去点率fc在 0.97左右,而对于按度数大小攻击引起平均路径长度突变的去点率 fc在 0.4左右,这说明公交站点网络对于度数攻击的鲁棒性较差.

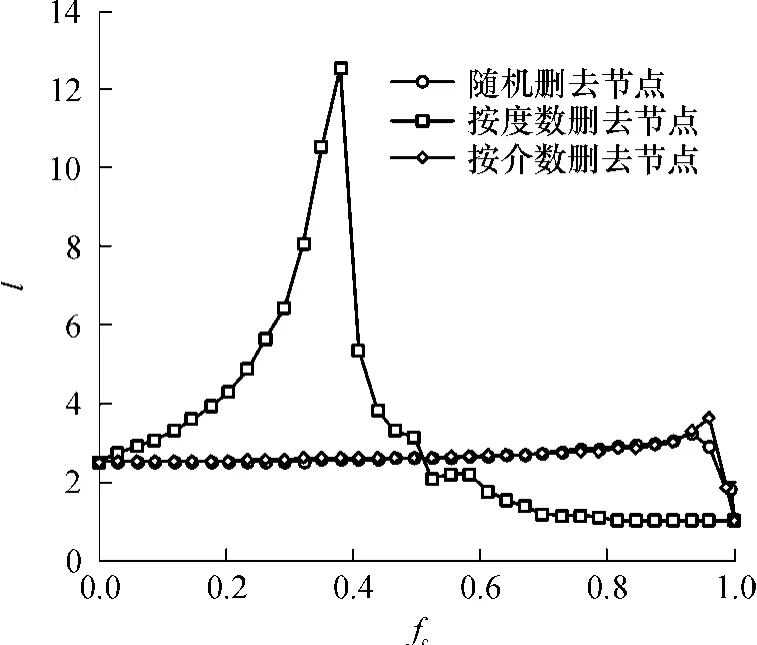
图8 公交站点网络的鲁棒性分析结果Fig.8 Robustness of transitstations network

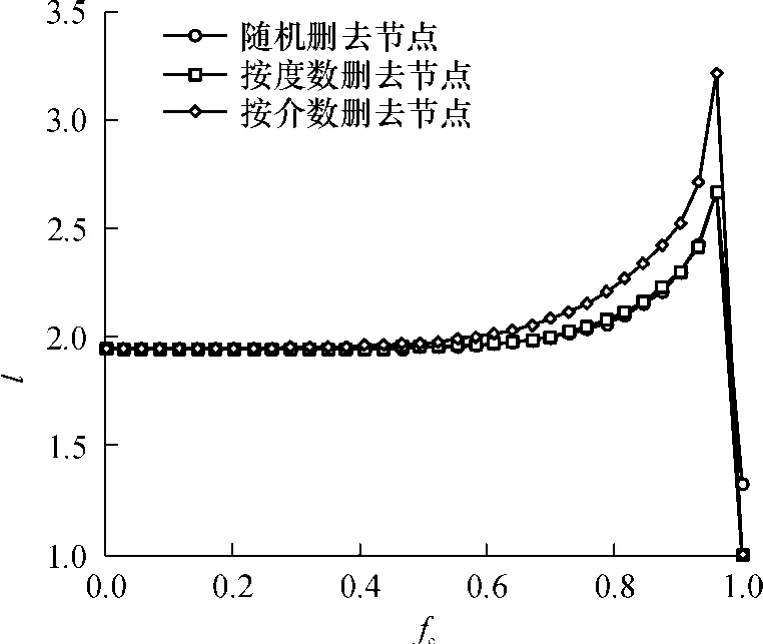
图9 公交站点随机网络鲁棒性分析结果Fig.9 Robustness of transit stations random network comparing

图9给出了随机网络相对于 3种攻击方式的平均路径长度的变化情况.比较图 8与 9,可以发现公交站点网络与随机网络相比,对于按度数大小删去节点的选择性攻击的鲁棒性要差很多.因此,在公交站点网络规划时,必须充分地注重对于哪些度数较大的节点进行较好规划,从而避免这类站点附近的拥堵而导致整个公交系统的运行效率下降.

5 结论

基于二分图模型,文中提出了城市公交网络的3种拓扑模型,定义了城市公交网络的拓扑结构鲁棒性指标,设计了针对大规模网络的鲁棒性分析的快速算法,并利用该算法对北京市公交系统的 3种网络模型的鲁棒性进行分析发现:公交网络与随机网络相比,其对于随机攻击方式的鲁棒性差别不大,但是对于按度数和按介数的攻击方式的鲁棒性要差于随机网络.该算法及结论可以用于实际的公交站点和路线规划设计.

[1] Wu J J,Gao Z Y,Sun H J,et al.Urban transit as a scale free network[J].Modern Physics Letter B,2004,18: 1043-1049.

[2] Albert R,Jeong H,Barabasi A L.Error and attack tolerance of comp lex networks[J].Nature,2000,406:378-382.

[3] Cohen R,Erez K,ben-Avraham D,et al.Resilience of the internet to random breakdowns[J].Phys Rev Lett,2000, 85(21):4626-4628.

[4] Cohen R,Erez K,ben-Avraham D,et al.Breakdown of the internet under intentional attack[J].Phys Rev Lett, 2001,86(16):3682-3686.

[5] Bollobas B,Riordan O.Robustness and vulnerability of scale-free random graphs[J].InternetMath,2003,1:1-35.

[6] 何胜学,范炳全.从公交线网的生成机理看复杂网络的多样性[J].系统工程学报,2007,22(6):599-606.

He Sheng-xue,Fan Bing-quan.From urban transit networks to various complex networks[J].Journal of Systems Engineering,2007,22(6):599-606.

[7] Newman M E J,Watts D J,Strogatz SH.Random graph models of social networks[J].Proceedings,National Academy of Sciences,2002,99(Supp l.1):2566-2572.

[8] Albert R,Barabási A L.Statistic mechanics of complex networks[J].Review of Modern Physics,2002,74:47-97.

[9] Von Ferber C,Holovatch Yu,Palchykov D.Scaling in public transport networks[J].Condens Matter Phys, 2005,8:225-234.