求解集送货可拆分车辆路径问题的启发式算法*

杨亚璪 靳文舟 郝小妮 田晟

(1.华南理工大学工商管理学院,广东广州 510640;2.华南理工大学土木与交通学院,广东广州 510640)

传统的车辆路径问题(VRP)是Dantzig和Ramser在研究亚特兰大炼油厂向各加油站投送汽油的运输路径优化问题时提出的,主要用于解决物流网络中任务点需求多样性的满足和服务车辆路径的安排,通常以车辆容量、行驶距离、服务时间窗等为约束条件,以运输成本(可包括时间、距离和费用成本等)最小为优化目标.在现实问题中,很多情况下存在着逆向物流的需求,一部分任务点需要送货,另一部分任务点需要集货,于是产生了带集货的车辆路径问题(VRPB)、装卸混合车辆路径问题(MVRPB)、同时送货和集货的车辆路径问题(VRPSDP),如果考虑时间窗、物流中心个数、随机需求等情况,问题的类型就会更加多样化[1-2].

上述问题有一个共同点,就是所有任务点只能接受一次服务,车辆大多数情况下处于非满载状态,任务点的集送货需求不可拆分,但物流服务中部分或全部任务点集送货需求量可能很大,车辆容量却很小,在一次访问中车辆无法完成任务,因此如何解决这类问题值得研究.

1989年Dror和Trudeau[3]提出了需求可拆分的车辆路径问题(SDVRP),为上述问题提供了解决思路,并指出允许需求拆分不仅可以节省服务距离,而且可以节省服务车辆数目,随后便有更多的学者投入到这方面的研究[4-8].对SDVRP进行再扩展就可以得到集送货可拆分的车辆路径问题(VRPSPDP),显然,VRPSPDP更具一般性,但目前只有Mitra[9-10]对VRPSPDP进行过探讨,构建了问题的混合整数线性规划模型,并先后给出了两种启发式算法.

文中将对VRPSPDP继续进行研究,借鉴Mitra给出的研究成果得到另一种启发式算法,最后通过算例对比3种算法的求解效果.

1 VRPSPDP数学模型

1.1 问题描述

VRPSPDP可以描述为:物流中心需要为多个任务点提供服务,不涉及物流服务的外包,各个任务点位置已知,同时具有送货和集货需求,且需求量可以超过车辆容量,车辆从物流中心出发,载运一定的货物到达任务点,采用先卸后装的方式完成任务,车内货物可以根据装卸货物的实际情况进行很好的位置调整,或者能够满足装卸货物的要求,任务点的集送货需求量可以拆分,由不同车辆或同一车辆多次完成,所有车辆保证途中不得超载,合理安排车辆的行驶路线,使得所有车辆的行驶距离之和最小.

基本假设:(1)物流中心只有一个,所有车辆从物流中心出发并最终回到物流中心;(2)配送车辆类型单一,数目事先确定,不再考虑因车辆数量变化而产生的总行驶距离减少;(3)任务点之间、任务点和物流中心之间均存在可连通的道路,点间距离已知,并且不存在方向性差异;(4)配送车辆没有时间窗和最大行驶距离等限制条件.

1.2 数学模型

设配送中心编号为 0,任务点编号为 1,2,…,n,车辆数为m;车辆容量为v;Dj、Rj分别为任务点j的送货需求量和集货需求量;D、R分别为任务点总的送货需求量和集货需求量;cij为任务点i和j之间的距离;xijk为车辆k从任务点i到j的次数;yij为从任务点i到j时车辆即将卸载的货物量(用于满足任务点的送货需求);zij为从任务点i到j时车辆已经装载的货物量(已经满足的任务点的集货需求).

完成任务所需要的车辆数为

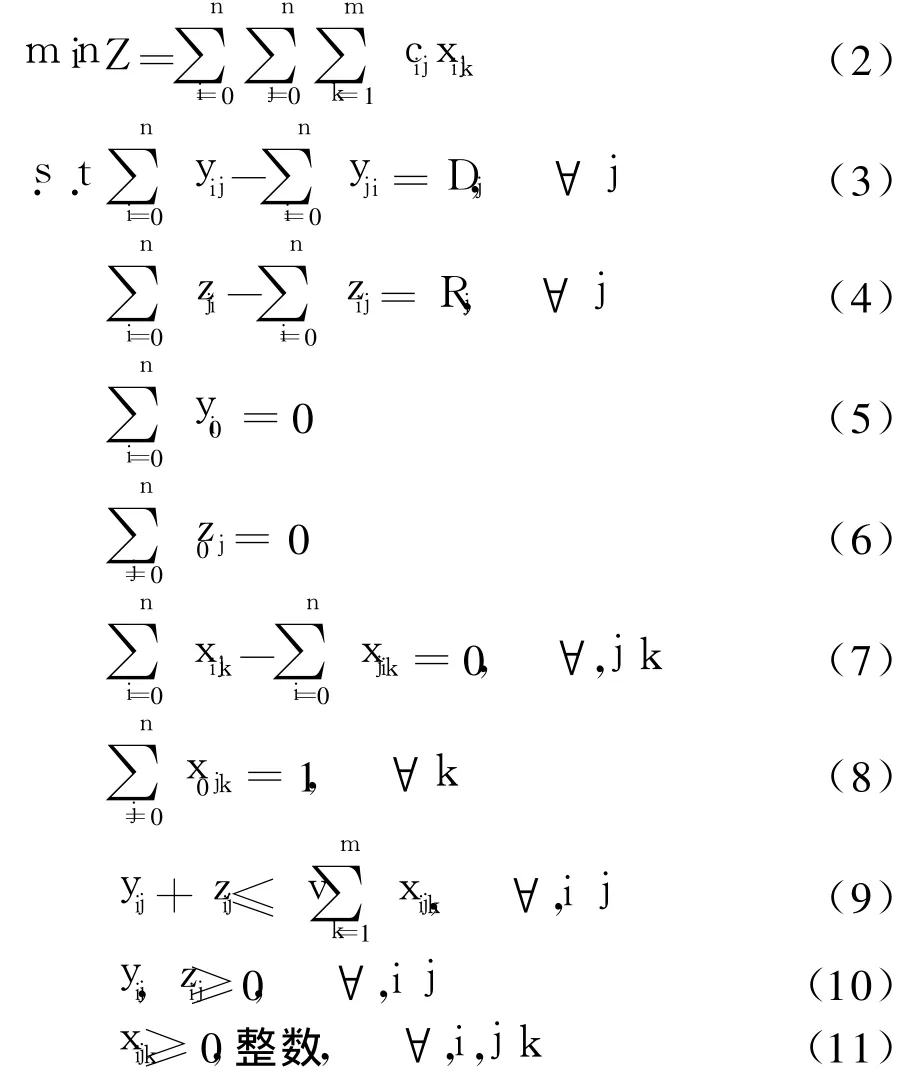
式(2)为目标函数,即所有车辆行驶距离之和最小;式(3)和(4)确保每个任务点的送货和集货需求得到满足;式(5)和(6)保证拟送出的货物不再运回物流中心,已收集的货物也不再从物流中心运出;式(7)表明车辆进出各个任务点的次数是平衡的;式(8)表示每辆车只从物流中心出来一次;式(9)保证车辆在执行任务的途中不超载;式(10)和(11)分别是对决策变量的非负约束和整数约束.

2 启发式算法

采用Mitra[9-10]解决VRPSPDP的思想,在已有算法的基础上进行改进.现以 FG表示车辆当前承载的拟送出的货物量,以RG表示车辆当前承载的已收集的货物量,以TC表示当前所有车辆的行驶距离之和.问题的求解可分为3个阶段:第 1阶段采用足够的车辆 m1完成各个任务点需要满载送货和满载集货的任务量(如图1(a)所示);第2阶段采用剩余车辆 m2完成剩余的任务量,可对各个任务点的集送货需求进行拆分(如图1(b)所示);第3阶段求出任务点之间、任务点与物流中心之间的最短距离,并用其替代现有线路上两点间的距离(如图1(c)所示).在各阶段运算过程中,需不断更新FG、RG和TC的值.

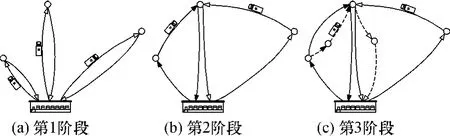
图1 启发式算法 3阶段示意图Fig.1 Scheme of three phases in heuristic algorithm实线箭头表示车辆的行驶路线,虚线箭头表示部分线路替换后车辆的行驶路线.

2.1 第1阶段算法

第1阶段派出m1辆车,其算法步骤如下:

(1)令i=1,m1=0,TC=0;

(2)考察任务点i,若Di≥v且Ri≥v,则派出一辆车满载货物访问该任务点,卸下货物并收集货物,满载返回物流中心,记录车辆行驶路线,更新 Di、Ri、D、R、TC,i=i+1,m1=m1+1,否则,i=i+1;

(3)若i≤n,转第(2)步;若i=n+1,考察所有任务点,若存在任务点j满足Dj≥v且Rj≥v,则令i=1,转第(2)步,否则,进入第2阶段.

2.2 第2阶段算法

第2阶段派出m2辆车,其算法步骤如下:

(1)令m2=m-m1,若D＜R,则否则,FG-max=v;

(2)若D≠0或R≠0,则转第(3)步,否则,进入第3阶段;

(3)若D≥FG-max,则FG=FG-max,否则, FG=D;

(4)若D＜R,转第(5)步,否则,转第(7)步;

(5)车辆从物流中心出发,找到最大 Ri对应的任务点i作为车辆访问的下一个任务点,即令next-dest=i,更新FG、RG、Di、Ri、D、R、TC,如果有多个任务点符合要求,则按任务点编号等待下一辆车访问;

(6)若RG≠v且R≠0,或FG≠0,则由当前任务点出发访问最近的任务点i(i必须存在集货或者送货需求),令next-dest=i,根据FG、RG、Di、Ri的关系,将点 i的集送货需求量进行合理拆分,并由车辆完成部分或全部集送货任务,更新FG、RG、Di、Ri、D、R、TC,如果有多个任务点与当前任务点距离相同,则按任务点编号优先访问集送货需求刚好满足的任务点,重复,直至RG=v或R=0,并且FG=0,车辆返回物流中心,记录其行驶路线,转第(2)步;

(7)车辆从物流中心出发,找到最大Di对应的任务点i作为访问的下一个任务点,即令next-dest=i,更新FG、RG、Di、Ri、D、R、TC,如果有多个任务点符合要求,则按任务点编号等待下一辆车访问;

(8)若FG≠0,或FG=0且R≠0,则由当前任务点出发访问最近的任务点i(i必须存在集货或者送货需求),令next-dest=i,根据FG、RG、Di、Ri的关系,将点 i的集送货需求量进行合理拆分,并由车辆完成部分或全部集送货任务,更新FG、RG、Di、Ri、D、R、TC,如果有多个任务点与当前任务点距离相同,则按任务点编号优先访问集送货需求刚好满足的任务点,重复,直至FG=0或R=0,车辆返回物流中心,记录其行驶路线,转第(2)步;

2.3 第3阶段算法

第3阶段实施部分线路替换,其算法步骤如下:

(1)对于点间距离不符合三角形各边大小关系的情况,利用最短路径算法,求出两两任务点之间、任务点和物流中心之间的最短距离;

(2)根据第(1)步的计算结果更新车辆行驶路线,保证各线路距离最短,算法结束.

3 算例分析

采用文献[9-10]中的算例,比较文中算法(这里称之为YH)与Mitra提出的两种算法(SM和NH)的优化效果.有 1个物流中心,19个任务点,车辆容量为 10个单位,各任务点集送货需求量见表 1第2、3列,根据点间距离分为两种情况.

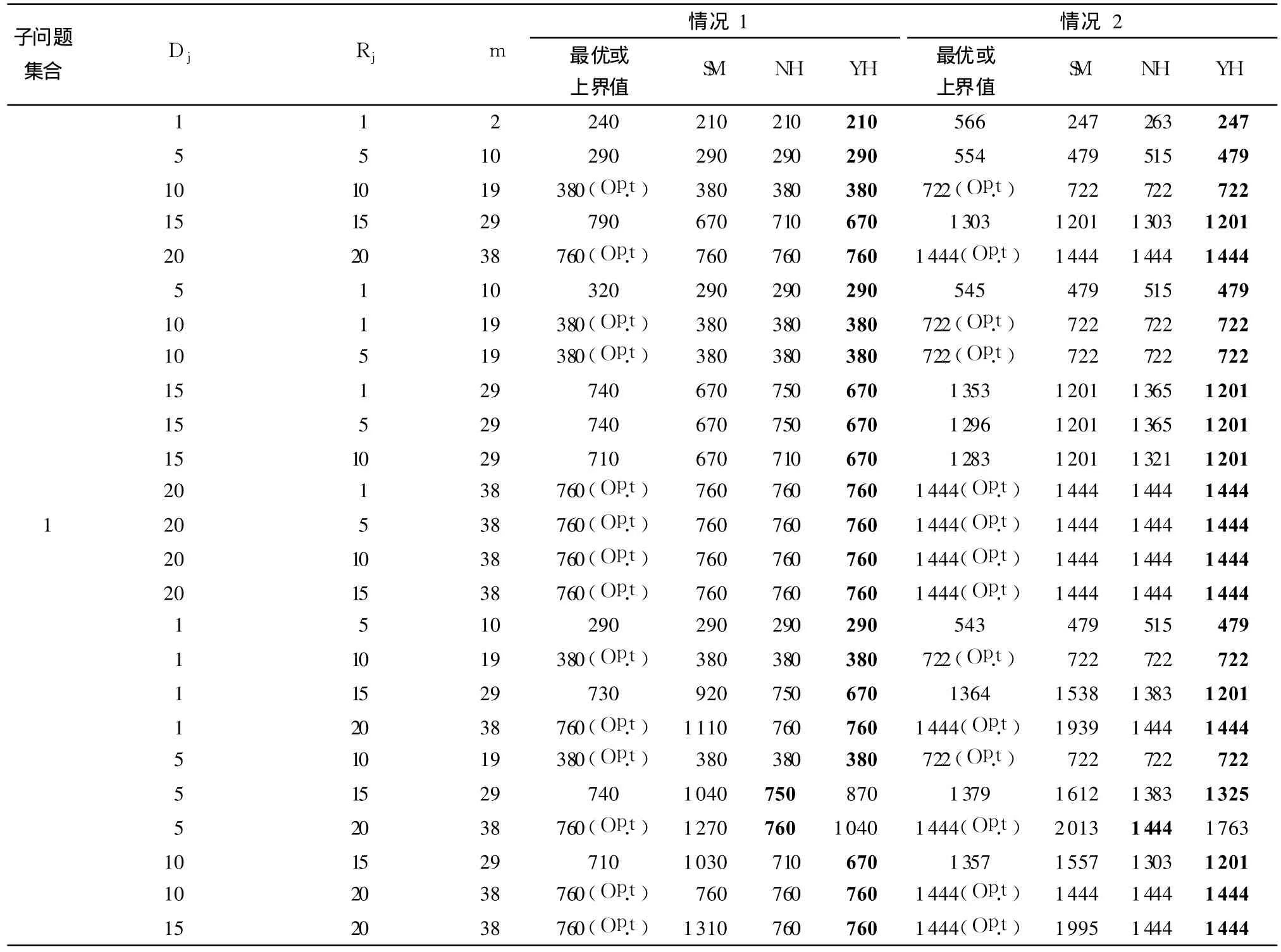
表1 3种启发式算法及CPLEX计算结果Tab le 1 Results of three heuristic algorithms and CPLEX

续表1

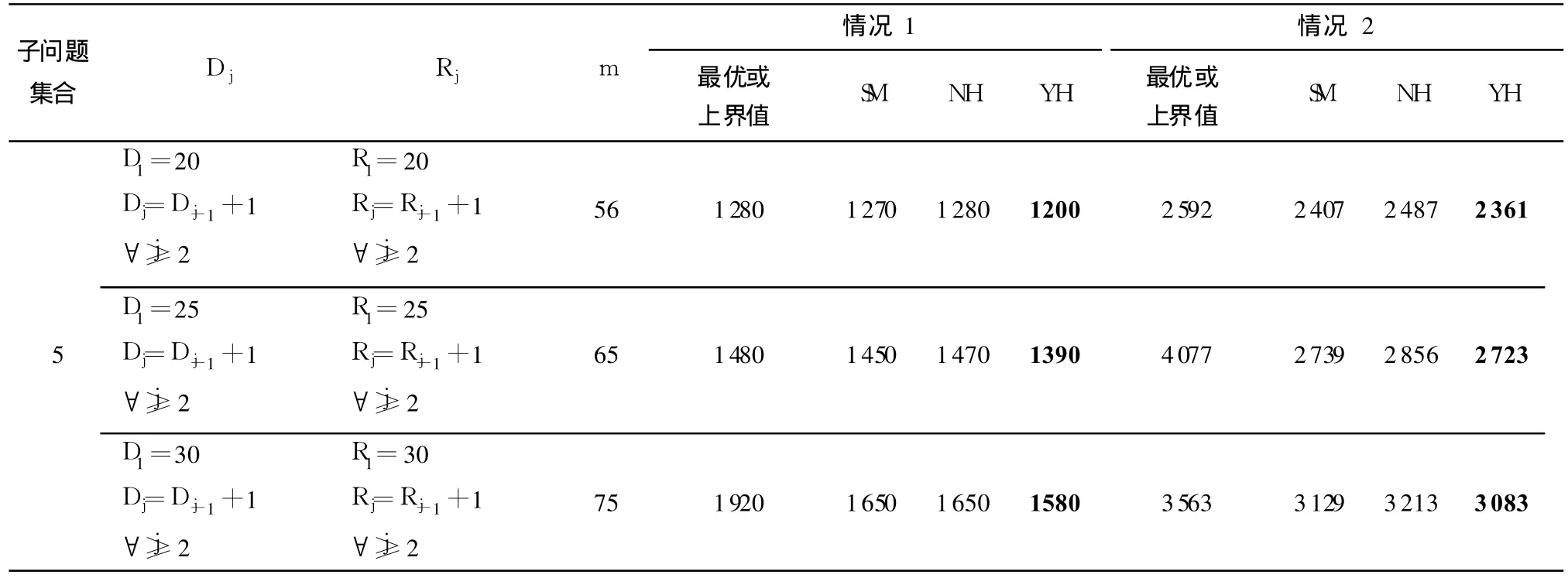
续表1

情况1:所有任务点之间的距离相等,cij=10,∀i,j(j＞i)并且cii=∞,∀i;

情况2:所有任务点之间的距离不相等,cij=9+ j-i,∀i,j(j＞i),并且cii=∞,∀i.

在情况 1和情况 2下,由各个任务点的集送货需求量变化和点间距的两种情况搭配,可以分别形成 55个子问题,共计 110个子问题,将其分为 5个子问题集合,采用 3种启发式算法及优化软件包CPLEX(部分子问题得到最优值,部分子问题运行30min得到上界值)分别计算,其结果对比见表 1,其中最佳优化结果用黑体字显示.

由计算结果可以看出,文中提出的启发式算法(YH)在大部分情况下优于SM和NH,并且可以获得最优解,但对于第 3类子问题集的优化效果略差,在实际应用中,可选择NH作为检验对比.

4 结语

以集送货可拆分的车辆路径问题为研究对象,提出了一种新的启发式算法.研究结果表明:新算法可以较好地求解VRPSPDP,尤其是在送货需求总量大于集货需求总量时其优化效果很好.实际物流服务过程中,在车型选择、货物堆载位置等方面应尽量考虑货物装卸混合带来的问题,以节约时间、提高服务效率.另外,文中研究尚未考虑车辆行驶线路长度、任务点间距离的方向性差异、客户对服务的时间窗、需求的随机性等问题,留待进一步探讨.

[1] Ropke S,Pisinger D.A unified heuristic for a large class of vehicle routing problemswith backhauls[J].European Journalof Operational Research,2006,171(3):750-775.

[2] Pisinger D,Ropke S.A general heuristic for vehicle routing problems[J].Computers＆Operations Research, 2007,34(8):2403-2435.

[3] Dror M,Trudeau P.Savings by split delivery routing[J]. Transportation Science,1989,23(2):141-145.

[4] Dror M,Laporte G,Trudeau P.Vehicle routing with split deliveries[J].Discrete Applied Mathematics,1994,50 (3):239-254.

[5] Mullaseril P A,Dror M,Leung J.Split-delivery routing heuristics in livestock feed distribution[J].The Journal of the Operational Research Society,1997,48(2):107-116.

[6] SiC,Bruce G,Edward W.The splitdelivery vehicle routing problem:app lications,algorithms,test problems,and computational results[J].Networks,2007,49(4):318-329.

[7] ArchettiC,Speranza M G,Hertz A.A tabu search algorithm for the split delivery vehicle routing prob lem[J]. Transportation Science,2006,40(1):64-73.

[8] Archetti C,Speranza M G,Savelsbergh M W P.An op tim ization-based heuristic for the split delivery vehicle routing problem[J].Transportation Science,2008,42(1):22-31.

[9] Mitra S.An algorithm for the generalized vehicle routing problem with backhauling[J].Asia-Pacific Journal of Operational Research,2005,22(2):153-169.

[10] Mitra S.A parallel clustering technique for the vehicle routing p rob lem with sp lit deliveries and pickups[J]. Journal of the Operational Research Society,2008,59 (11):1532-1546.