基于计算流体动力学的S型风力机性能分析
徐小韵,郑 源,赵振宙,刘文明
(河海大学水利水电学院,江苏南京 210098)
Savonius风力机是典型的阻力型垂直轴风力机,由芬兰萨沃纽斯(Savonius)于20世纪30年代发明[1],两半圆叶片交错成S形,简称为S型风力机.S型风力机因转速较低,风能利用系数(Cp≈0.15)低于水平轴风力机(Cp≈0.45)和达里厄垂直轴风力机(Cp≈0.35)而发展缓慢[2-3].但S型风力机具有结构简单、造价便宜、维修及安装方便、无需调风装置和启动力矩大等优点[4-6],因此近年来诸多学者主要从叶片个数、偏心距、上下盖板几个方面[7-9]对其进行研究,以提高其风能利用系数.
此外,关于风力机叶片几何尺寸(包括叶片直径d,旋转直径D,叶片高度H)的研究主要集中在原模型的对比实验上,而对于高度直径比研究甚少.如,最初Savonius[1]通过对比30多种叶片几何尺寸,在风洞和自然风下进行风力机的模型和原型测试,得出相同风速下,风力机在自然风中转速更高的结果.随后,Bach[10]对S型风力机也进行了相关研究,所得最高风能利用率为0.24.Newmann[11]在改变叶片几何尺寸进行风力机性能对比实验和数值计算时,发现风洞对测试结果有一定的干扰,风力机原型的性能与模型测试结果存在偏差,得到的最高风能利用率为0.20.
Menet等[12-13]的研究表明,增加叶片高度可以提高S型风力机的单位宽度功率,对改善风力机的性能有一定的影响.因此,本文以单位宽度功率为指标,探讨了高度对S型风力机性能的影响规律,采用计算流体动力学(computational fluid dynamics,CFD)技术对风力机进行数值模拟,分析了在等过风面积和等直径2种工况下叶片高度对单位宽度功率的影响.
1 风能理论与L-σ准则
1.1 风能理论
风能利用系数Cp为风力机输出功率与风能的比值:

其中
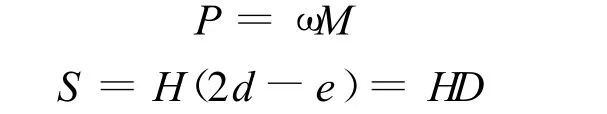
式中:P——风力机输出功率,W;S——风力机过风面积,m2;ρ——空气密度,通常取1.25 kg/m3;c——风速,m/s;ω——叶片角速度,r/min;M——力矩,N◦m;e——偏心距,m;d——叶片直径,m;D——风力机旋转直径,m;H——叶片高度,m.
尖速比λ为叶片线速度与来流风速的比值:

式中R为风力机旋转半径,m.
力矩系数Cm为

1.2 L-σ准则
L-σ准则[12-13]是相同机械应力下水平轴与垂直轴风力机单位宽度功率的比较准则,其中,L为过风面积的宽度,即风力机的旋转直径D,σ为叶片的机械应力.该准则提出了单位宽度功率的概念(即风力机垂直于迎风面单位宽度上的功率),指出风力机在考虑叶片所受机械应力时,相比其他高转速的风力机,S型风力机单位宽度功率更大.单位宽度功率为
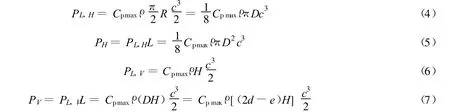
式中:PH,PL,H——水平轴功率和单位宽度功率;PV,PL,V——垂直轴功率和单位宽度功率;Cpmax——理论上风力机能达到的最大风能利用系数.从式(5)和式(7)可看出,PH仅与D有关,而PV还与H有关.同时,在偏心距e一定时,PV由叶片直径d和叶片高度H共同决定.因此,叶片高度与直径之比α(简称高径比)对S型风力机单位宽度功率及风能利用系数有影响.
2 数值优化
2.1 数学模型
Saha等[14]通过实验证明,k-ε双方程模型适用于S型风力机流场的研究.因此,采用标准k-ε湍流模型对叶片周围流场进行模拟,湍动能k和湍动能耗散速度ε的模型方程分别为
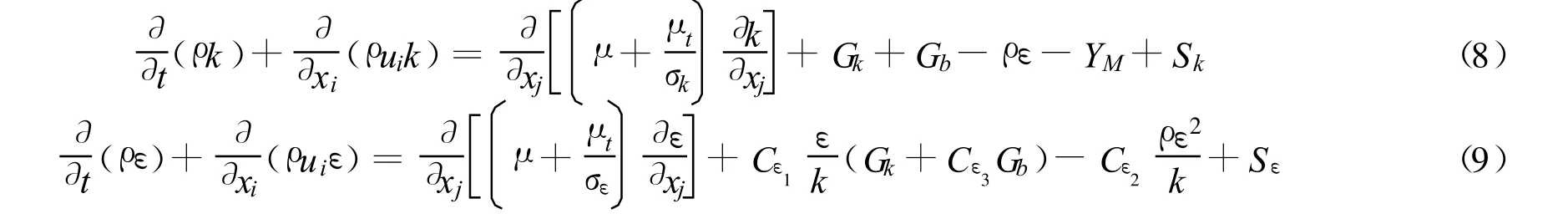
式中:Gk——由于平均速度梯度引起的湍动能k的产生项;Gb——由于浮力引起的湍动能 k的产生项; YM——可压湍流中脉动扩张的贡献;Cε1,Cε2,Cε3——经验常数;σk,σε——与湍动能 k和耗散率ε对应的Prandtl数;Sk,Sε——用户定义的源项.
流体材料设为理想气体,求解基于Reynolds平均的N-S不可压无黏方程[15]
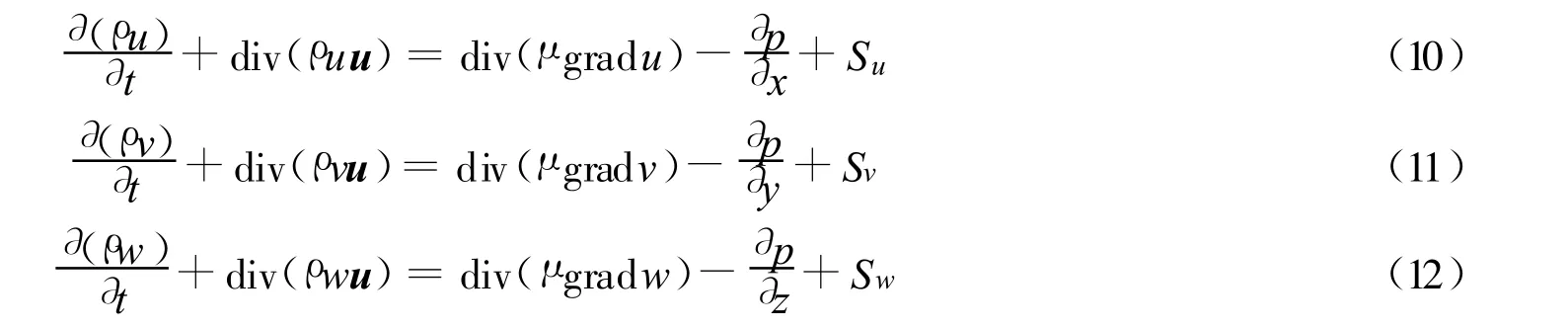
式中:ρ——密度;p——流体微元体上的压力;μ——动力黏度;u——速度矢量;Su,Sv,Sw——动量方程的广义源项.
2.2 风力机模型及网格划分
风力机由2个叶片组成,如图1(a)所示,叶片直径d=1.8m,厚度2mm,偏心距e=0.3d.采用Gambit软件建立三维模型,网格类型为TGrid,如图1(b)所示.计算过程中,采用区域加密方法对叶片区域流场网格进一步加密,网格总数超过200万.
2.3 计算方法及边界条件
采用SIMPLE算法求解压力耦合方程,二阶迎风离散格式[16],收敛残差标准为10-5.如图1(b)所示,进口(区域1)采用速度边界条件,风速设为9m/s,出口(区域2)采用自由扩展边界条件,叶片区域流体为旋转流体,叶片采用相对旋转固体壁面边界条件.
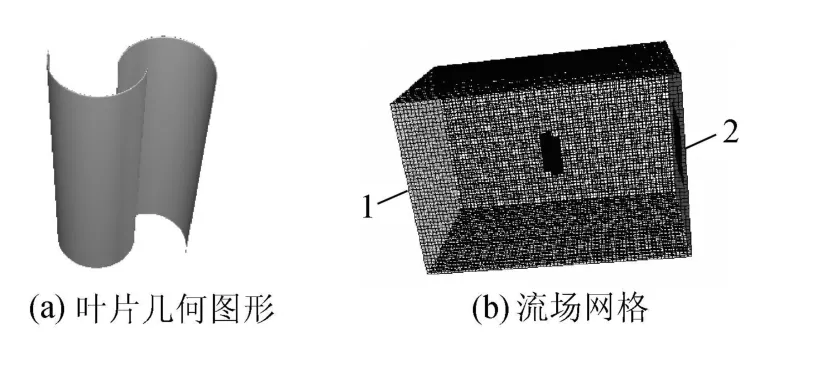
图1 S型风力机结构Fig.1 Structure of Savonius rotor
3 优化结果
3.1 等过风面积下不同高径比的对比
图2显示了等过风面积工况下不同高径比α对风力机性能的影响.P和PL随α的变化规律如图2(a)所示.由L-σ准则可得,增加叶片高度可以提高单位宽度功率;在相同过风面积下,单位宽度功率随高径比的增加而增加,但叶片直径减小;当单位宽度功率增加速度大于叶片直径减小速度时,风力机的输出功率增加.因此,在高径比1~6范围内,P和PL随α的增加而增加.
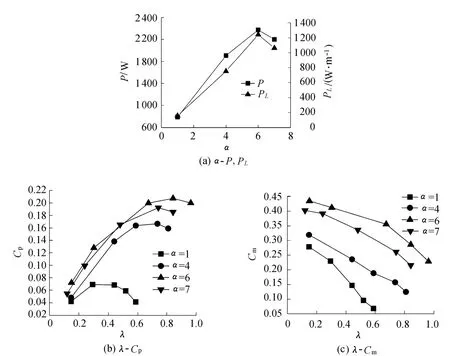
图2 等过风面积下不同高径比对S型叶片的影响Fig.2 Influence of different height-diameter ratios on Savonius rotor in same wind area
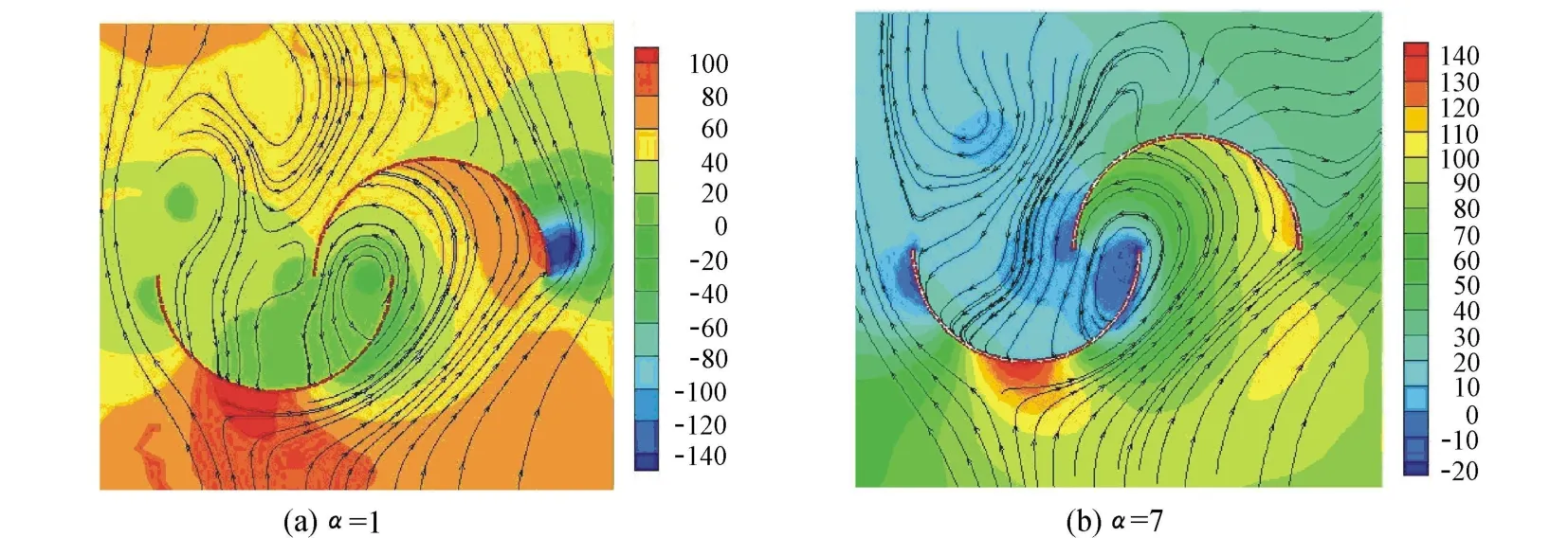
图3 等过风面积下叶片的压力云图(单位:Pa)Fig.3 Pressure nephograms for blades in same wind area(units:Pa)
当高径比继续增加,叶片半圆直径过小,气流急速转弯易造成旋涡或脱离,引起有效功的损失,如图3所示.因此,当α>6时,P和PL随α的增加而减小;当 α=6时,P和PL有最大值,分别为2 371.16 W和1241.45W/m.因此,在等过风面积工况下,单位宽度功率和总功率随高度增加而先上升后减小,α=6为该工况下的最佳高径比.
同时,在过风面积相同时,风能利用系数与风力机输出的功率成正比,因此,在 α=6时,Cp有最大值0.2,如图2(b)所示.此外,由图2(c)可知,在尖速比0~1范围内,力矩系数在α=6时最大.
3.2 等叶片直径下不同叶片高度的对比
在保持叶片直径不变的条件下,分别取α=1,4,6,7,比较叶片高度对单位宽度功率的影响,计算结果如表1所示.当叶片直径不变时,增加叶片高度可以提高单位宽度功率,从而增加输出的总功率,但过风面积也随叶片高度增加而增加;当功率的增加速度大于过风面积的增加速度,即单位宽度功率的增加速度大于叶片高度的增加速度时,风能利用系数上升.从表1可看出,PL的变化规律与等过风面积工况下类似.随叶片高度增加,PL先增大后减小,在 α=6时,即叶片高度为10.8m时,PL有最大值560.96W/m.
从表1可看出,当α=6时,风力机性能最佳,风能利用系数Cp有最大值0.20,力矩系数Cm达0.27,两者变化趋势相近.
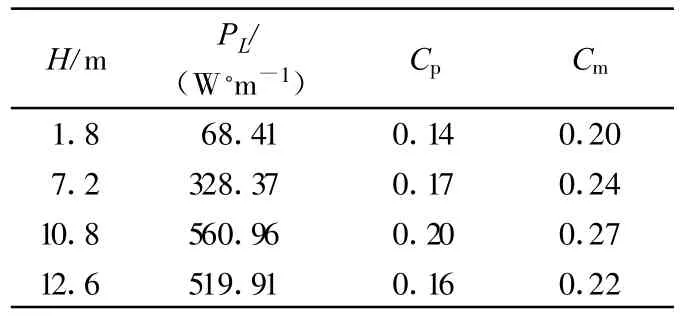
表1 等叶片直径下叶片高度变化对S型叶片的影响Table 1 Influence of different blade heights on Savonius rotor with same diameter of blades
4 结 语
采用计算流体动力学技术,通过增加叶片高度来提高单位宽度功率的方法,分析了叶片高度对风力机性能的影响.等过风面积工况下,侧重模拟叶片高度与直径之比对单位宽度功率和总功率的影响;等叶片直径工况下,主要计算叶片高度对单位宽度功率增加速度的影响.在所取的4个高径比系列中,S型风力机在α= 6时单位宽度功率达到最大值,与Menet提出的从增加高度来提高单位宽度功率的可行方案吻合;当 α=6时,风力机的风能利用系数最大,表明增加叶片高度对风力机的性能起到一定的改善作用.
[1]SAVONIUS S J.The S-rotor and its application[J].Mechanical Engineering,1931,53(5):333-338.
[2]TWIDWELL J W,WEIR A D.Renewable energy resources[M].Cambridge,Britain:The University Press Cambridge,1985:411.
[3]ELDRIDGE F R.Windmachines[M].New York:VanNostrand,1980:214.
[4]熊礼俭.风力发电新技术与发电工程设计、运行、维护及标准规范实用手册[M].北京:中国科技文化出版社,2006.
[5]张国铭.论制造兆瓦级垂直轴风力发电机的合理性[J].风力发电,2001,9(4):25-29.(ZHANG Guo-ming.Rationality of generator manufacturing on the megawatt level vertical axis windgenerator[J].Wind Power,2001,9(4):25-29.(in Chinese))
[6]孙云峰,田德.垂直轴风力发电机的发展概况及趋势[J].农村牧区机械化,2008,10(2):42-44.(SUN Yun-feng,TIAN De. Trends and development overview of vertical axis wind turbine[J].Mechanization in Rural&Pastoral Areas,2008,10(2):42-44.(in Chinese))
[7]SHELDAHL R E,FELTZ L V BLACKWELL B F.Wind tunnel performance data for two and three bucket Savonius rotor[J].Journal of Energy,1987,2(3):160-164.
[8]MODI V J,FER MANDO M S U K.On the performance of the Savoniuswind turbine[J].Journal of Solar Energy Engineering Transactions of the ASME,1989,111(5):71-81.
[9]MOJOLA O O,ONAZANYA O E.Performance testing of a Savoniuswindmill rotor in shear flows[J].Wind Engineering,1984,8(2):109 -121.
[10]BACH G.Investigation concerning Savonius rotors and related machine[M].Quebec,Canada:Brace Research Institute Press,1931.
[11]NEWMAN B G.Measurement on a Savonius rotor with variable gap[R].Sherbrook,Canada:Sherbrook University,1994:116-118.
[12]MENET J L,VALDES L C,MENART B.A comparative calculation of the wind turbines capacities on the basis of the L-σcriterion[J]. Renewable Energy,2001,22(4):491-506.
[13]MENET J L,MENART B.Une proc édure comparison de quelqueséoliennes classiques basée surl/utilisation du critère L-sigma[C]// Nancy In Proceedings of 15thFrenchMech Symp 2001.[S.l.]:XVème Congr ès Francais de Mécanique,2001:352-358.
[14]SAHA U K,RAJKUMAR M J.On the performance analysis of Savonius rotor with twister blades[J].Renewable Energy,2006,31(8): 1776-1788.
[15]VERSTEEG H K,MALALASEKERA W.An Introduction to computational fluid dynamics:the finite volume method[M].New York: Wiley,1995.
[16]PATANKER S V,SPALDING D B.A calculation processure for heat,mass and momentum transfer in three-dimensional parabolic flows [J].Int J Heat Mass Transfer,1972,15(9):1787-1806.
河海大学学报(自然科学版)2010年3期
