循环平稳特性检测频域设计及信噪比估计研究*
(哈尔滨工业大学 通信技术研究所,黑龙江 哈尔滨150080)
近年来,随着无线通信技术的飞速发展,频谱资源日益匮乏。这是由于当前频谱资源的平均利用率非常低,且极不平衡造成的[1]。由于目前的频谱分配政策是建立在固定频率的基础上的,因此大部分频谱被分配给了授权频段应用,而非授权频段上由于大部分新兴无线电技术占用而过度拥挤。认知无线电技术即是为了提高频谱利用率,进行动态频谱分配而产生的。认知无线电技术通过感知外界环境,检测授权用户频段中的空闲频谱,从而实现认知用户的动态接入和实时通信。认知过程包括3个步骤:频谱感知、频谱分析和频谱决策[2]。
频谱感知是认知无线电技术的首要任务,它是实现频谱管理和频谱共享的前提。所谓感知,就是在时域、频域和空域多维空间,对被分配给授权用户的频谱进行检测,检测这些授权频段内是否有授权用户工作,从而得到频谱使用情况。如果该频段未被授权用户使用,认知用户即可临时使用。频谱感知的目的就是发现频谱空穴让认知用户使用此频段,同时在授权用户占用该频段时及时退出,选择其他的空闲频谱进行不中断的通信。认知用户在频段切换过程中不能对授权用户造成干扰,这就需要频谱感知的精确性和实时性。频谱感知技术可以归结为发射机检测、合作检测和基于干扰的检测[3]。现有的频谱检测方法主要包括能量检测法、循环平稳特征检测法、高阶谱检测法以及协作检测法[4]等。本文针对循环平稳特征检测时域设计法计算周期长、设备比较复杂、实时性不高等不足,根据离散傅里叶变化的特性提出了频域设计循环平稳特征检测的方法,不仅有效地降低了计算量,提高了系统的实时性,同时也大大节省了存储空间。此外,提出了利用统计原理对未知信道的信噪比利用积累量方差进行了有效的估计,从而可以根据信道的信噪比选择最合适的信号检测方法。
1 频域法循环平稳特征检测实现
在通信系统中,由于对信号进行调制、采样、编码等,使得信号的统计特性呈现周期性变化。所以调制信号具有典型的循环平稳特性[5],可利用其循环谱密度函数特征完成其检测及参数估计。在实际对信号进行分析时,为了先产生循环自相关函数,再求循环谱密度,通常先将接收的信号序列乘以一个旋转因子,分别生成x(t)ejπαt和 x(t)ejπαt。然后求出对应循环频率的循环自相关函数的估计值,最后进行离散傅里叶变换,求出对应循环频率时的循环谱密度。
现有算法基本都是利用时域法实现信号的循环谱检测[6]。因为对时域直接进行运算方法简单,所乘的旋转因子利用欧拉公式将实数域与复数域所得的结果分别存储即可。但是正弦和余弦函数的数值计算通常利用泰勒公式进行近似,因此计算的周期较长,系统比较复杂且实时性不高。为了提高信号检测的实时性,本文考虑频域计算的方法,利用离散傅里叶变换中时域乘以一个旋转因子就相当于在频域进行循环位移的性质,只需要将经过离散傅里叶变换后的序列进行循环位移,单用移位寄存器即可实现,相对于计算正弦和余弦函数简单得多。由于采样点的个数是2的正整数次幂,因此进行离散傅里叶变换只需将原序列进行若干个基二的离散傅里叶变换,将这些基二的离散傅里叶变换的结果顺序排列即可。由于原序列是实数序列,所以变换后的序列必定为实数序列,这样做同时也节省了一半的存储空间。之后再将循环位移后的序列进行离散傅里叶反变换,得到的序列相当于信号的采样序列与一个旋转因子相乘所得的序列。图1(a)和(b)是分别利用时域法和频域法对信号进行处理的程序流程图。
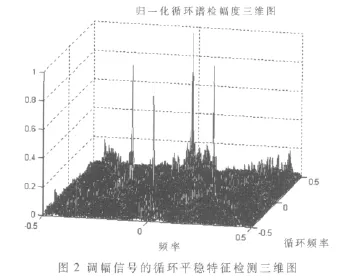
当存在噪声时,频谱特性中的峰值逐渐变得不明显。随着信噪比的降低,分辨能力也逐渐下降。对一定的载波频率和信号频率以及调制系数的调制信号的频谱在不同的信噪比条件下进行仿真,图2为对调幅信号进行循环平稳特征检测时各个频率和循环频率对应的幅度值三维图。由图可以看出,对于调幅信号,在频率轴上以正负载波频率为中心,在循环频率轴上以正负二倍载波频率为中心的4个点处循环谱密度计算结果出现峰值,这与理论分析结果是相符的。
2 信噪比估计
对于实际信号如果预先不知道信噪比,单从个别检测结果来看比较难判断实际的信噪比,因此很难判定应用哪种信号检测方法最合适。但是对于一定次数的检测,可以从统计规律对信噪比进行有效的估计,从而确定所采取的检测方法。

图1 循环谱密度程序流程图
理论分析可知多次检测结果中,有信号时检测结果的统计均值和方差与信噪比有着必然的联系。为了分析的方便和实用性,本文对能量检测和周期平稳过程检测分别采用10次独立的检测结果进行方差分析。在仿真中本文假设信噪比参数分别为SNR=[-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0]dB,采样点分别为 256和 1 024时对应各信噪比时的方差幅度值,仿真结果如图3所示。因为采样点数越多,积累的信噪比越高,所以由图3(a)和图3(c)可见,当信噪比较高时,各次检测结果的频带内能量累积量相差不大,因此方差较小;相反,当信噪比降低时,由于各次检测结果的频带内能量累积量的不确定性增大,因此方差急剧增大。同时由图3(a)和图3(b)可以发现,当采样点数相同,独立检测次数增加时,所得到的方差幅度曲线变得平缓,这是由于多次检测使得频带内方差累积量确定性增强的原因。虽然多次检测能提高检测的精度,但同时复杂度也会有所提高。

然而只知道方差和信噪比的定性关系还不够,因为在实际检测中,如果想通过计算方差对实际信噪比有一个较为准确的估计,还需要依赖于方差与信噪比之间的定量关系。
由理论分析可知,方差和信噪比之间是某种线性关系。在不同的信噪比条件下,对10次独立的检测结果进行方差幅度值分析,然后将结果都表示成分贝形式,从图3(d)中可以看出方差分贝幅度与信噪比成近似线性关系。然后利用最小二乘法对图3(d)中数据进行回归分析,求出直线的斜率和截距,以及置信区间。其中置信区间取概率为0.95以上的范围。应用上述方法对数据进行处理和分析,将经过处理的数据用数学表达式描述,即可得到方差和信噪比关系,如表1所示。同时由于以上分析是建立在接收信号能量一定的假设下,因此在分析中对相应的信噪比得出的方差计算值均遵循此假设。
从表1可以看出,当采用能量检测法进行信号检测时,有信号与无信号时计算的方差差异较大。因此仅仅计算方差还不能判断是高信噪比时有信号还是低信噪比无信号,还需要借助均值来判断。而如果采用周期平稳过程特征检测方法进行计算,当循环频率为二倍载频时,利用合理的采样点次数积累计算的方差结果只与信噪比成近似线性关系,而与信号有无没有关系。同时从图3(c)和图3(d)中可以看出,当采用周期平稳过程特征检测法时,有信号和无信号时的曲线几乎重合,在图上不能分辨;而用能量检测法在同样的信噪比下,信号有无对若干次独立采样积累计算的方差结果影响很大。因此在信噪比预先不确定的情况下,可以采取周期平稳过程特征检测方法通过方差的值准确估计出信噪比。
循环平稳特征检测法是频谱检测中的重要方法。本文针对现有的循环平稳特征检测时域设计法计算周期较长,设备比较复杂,实时性不高等不足根据离散傅里叶变化的特性提出了一种循环平稳特征检测频域设计方案。此方法具有与时域法相当的检测能力,但是有效地降低了计算量,提高了系统的实时性,还大大节省了存储单元。同时本文利用统计规律得出累计方差值和信噪比之间的近似线性关系,通过最小二乘法对其分析,对信噪比进行了有效的估计,从而还可选择更合适的信号检测方法进行频谱感知。

表1 不同情形的检测结果的方差与信噪比的数学关系
[1]FCC.ET Docket No.03-222 notice of proposedrulemaking and order.December,2003.
[2]THOMAS R W,DASILVA L A,MACKENZIE A B.Cognitive networks.IEEE DySPAN 2005,2005:352-360.
[3]AKYILDIZ I F,LEE W Y,VURAN M C.Next generation/dynamic spectrum access/cognitive radio wireless networks.A survey,computer networks50,2006:2127-2159.
[4]刘玉涛,谭学治.认知无线电及其原始用户检测.通信技术,2008(01):49-51
[5]CLAUDIO R C M S,CHOI B,KIM K.Distributed spectrum sensing for cognitive radio systems.Blacksburg,VA USA 24061.
[6]DAVID K,ANUJ S.Cyclostationary processes on shape spaces for gait-based recognition[J].Lecture Notes in Computer Science,2006,12(1):442-453.

