维修员工数量配置的优化模型

王新田，尹树华，李江红，孙岩清

（1.西安通信学院 陕 西 西 安 7 10106；2.通信指挥学院， 湖北 武 汉 4 30010）

合理配置部门的员工数可以减轻成本，提高效率[1]。在对维修人员的安排上，人员过多往往导致资源利用率低；而人员过少，满负荷工作，则导致员工过累。这种情形其实是人员的安排和维修客户需求的矛盾，是生产能力和客户需求不匹配的表现。因此需采用科学的方法建立数学模型，合理安排维修人员的数目，实现资源利用的最高配置。

1 排队论模型及其主要指标

1.1 排队论模型简介

排队论是指：顾客请求使用一个特定的服务装置（服务员），如果某个服务装置是可利用的，来到的顾客便占用它并使用某个时间长度。之后顾客离开系统，而服务装置立即恢复为可利用的，而去服务于刚来或者等待的顾客。如果一个到来的顾客发现没有可利用的服务装置，他将采取等待或者离去的行动之一[2]。这样的模型称为随机服务系统。研究随机服务系统的理论称为排队论。在本系统中，可将维修的装备作为顾客，维修人员作为服务装置。这可以看作是一个单排队多通道服务的排队系统，其排队模型如图1所示。

图1 维修单排队多服务系统

1.2 主要指标

排队长：指在系统中排队等待服务的所有顾客数，其期望值记作Lq。等待时间：指一个顾客在排队系统中排队等待的时间，其期望值记作Wq。忙期：指服务机构连续繁忙的时间长度（从顾客到达空闲的服务机构起到服务机构再次空闲止这段时间的长度），记作Tb。服务强度：表示在相同时间间隔内，到达顾客的平均数与承受完服务的顾客平均数之比。反映服务效率和服务机构的利用程度[3]。

2 模型的建立和求解

2.1 模型的建立

这是一个单排队多服务的排队模型，即到达间隔为负指数分布[4],服务时间也为负指数分布，c个服务台,顾客源无限,系统容量也无限,先到先服务排队系统[5]。可采用M/M/c/∞/∞求解。其中M表示顾客相继到达间隔时间的分布和维修人员服务时间的分布，c是指维修人员的数目。由于顾客可以是源源不断的，假设顾客流为泊松流，平均到达率为λ。各维修人员的服务时间满足负指数分布，而各维修人员的工作是相互独立的(不搞协作)，单个维修人员的平均服务率为μ，则整个服务机构的平均服务率为cμ（当n≥c），或nμ（当n＜c）。令ρ=λ/（cμ）， 称为系统的服务强度（服务机构的平均利用率），当ρ＞1时，系统就会出现排队现象，即有顾客在排队等待。随着时间推移，队伍会越来越长，系统就越来越不稳定，具体表现就是顾客会对部门产生不满，因此不能采纳。当ρ≤1时，并且时间充分，每个状态将会循环出现[6]。系统状态概率为：

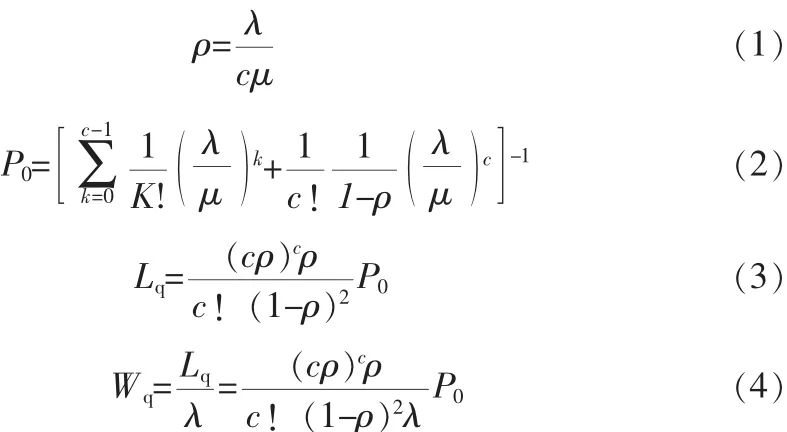
通过连续10天的跟踪调查得到数据，如表1所列。

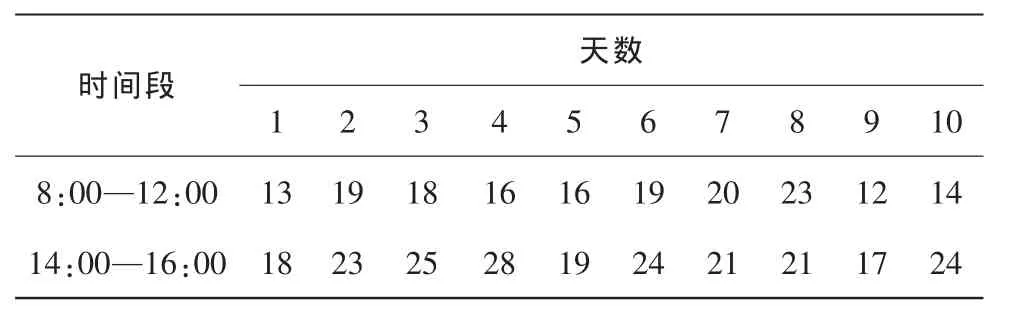
表1 顾客维修情况统计表

从表1中看到顾客的到达时间划分为2段，这有利于对员工的工作时间进行安排。上午的工作时间中，顾客的到达平均数为17人。平均每小时是4.25人。下午的工作时间中，顾客的到达平均数为22人。平均每小时是5.5人。下午的顾客数相比上午较多。但部门在上午和下午都是安排3个维修人员。每个维修人员每半个工作日只能服务8个客户。则每个员工的服务率为2人/h。这样必然导致下午的工作人员工作强度比较大。而且会出现排队等待的现象。下面运用排队论模型对维修人员的安排进行建模，合理配置人员。

2.2 模型求解

从建立的模型得到上午的顾客期望值λ=4.25人/h，下午顾客的期望值λ=5.5人/h。每个维修人员的平均服务率λ=2人/h。维修人员数c=3。这里需要求出维修台的平均服务强度ρ，在系统中排队等待服务的所有顾客数Lq，顾客在排队系统中排队等待的时间Wq。根据这3个指标得出这个系统中顾客平均需等待的时间，每个维修员工的忙闲程度，从而得出员工的安排是否发挥了最大的利用率，顾客是否对服务满意。由式（1）～式（4）得出：

1）上午工作时段

ρ=λ/（cμ）=0.708，λ/μ=2.125。利用LINGO软件来求解，有关参数为c=3，L=λ=4.25，T=1/μ=1/2，R=λ/μ=2.125。其编程为：

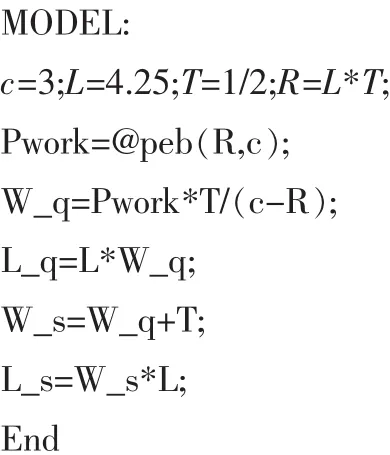
运行该程序得Lq=1.226，Wq=17 min。

2）下午工作时段

ρ=λ/（cμ）=0.917，λ/μ=2.75。利用LINGO软件来求解，有关参数为c=3,L=λ=5.5,T=1/μ=1/2，R=λ/μ=2.75。其编程为：

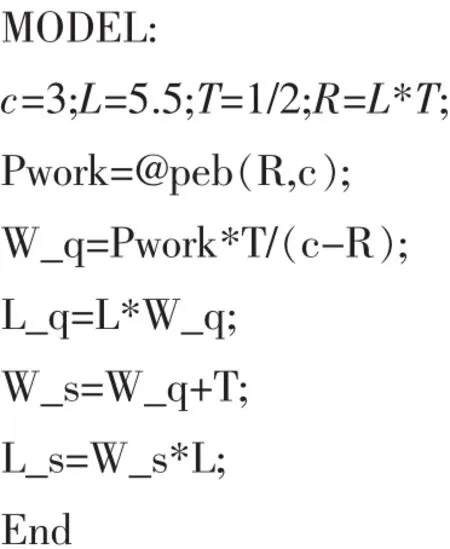
运行该程序得Lq=9.31，Wq=1.69 h。

从计算结果可以看出，员工上午的平均工作强度为0.708，强度有点偏低，顾客的等待时间为17 min，这在维修一些比较大的机器时是可以忍受的。而员工下午的平均工作强度为0.917，强度很大，基本上得不到休息，而顾客的等待时间竟然为1.69 h，远远超出顾客忍受程度，所以必须调整员工人数。

在不同的时间段设置不同数目的员工，利用前面的计算方法，得到结果如表2所示。

表2 系统维修指标表

从表2可知，当配置2个员工时，服务强度ρ＞1，这时将出现排队无穷尽的情况，所以不适用。当配置3个员工时，上午时段，每个顾客的等待时间为17 min，服务强度ρ为0.708，可以接受；下午时段，每个顾客的等待时间为101 min，显然不能接受。当配置4个员工时，上午时段，每个顾客等待时间为3 min，服务强度为0.531，员工空闲时间太多，资源利用率不高，应该舍弃；下午时间段，顾客等待时间为10 min，服务强度ρ为0.688，可以接受。当配置5个以上的员工时，服务强度小于0.5，不适合。由以上看出，上午时间段，应该配置3个员工。而下午时间段，配置4个员工比较合理。

综上可知，对于维修部门的员工配置，重点参考2个指标：顾客平均需等待的时间Wq和每个维修员工的忙闲程度ρ。通过观察平均到达的顾客数和员工的维修时间，得出λ和μ，并利用上述编程进行简单的数字替换，得到合适的员工数目。

3 结束语

综上所述，利用排队论模型M/M/c/∞/∞，通过对顾客的数目和员工的维修时间进行观察，结合模型，得出各个参考指标，进而求出最佳的维修人员的数量。从而可以对维修部门的员工配置进行合理安排，这样既方便顾客，又考虑到部门的人力资源利用率。

[1]廖业红.运筹学排队论在客户服务中的应用与辅助决策[J].商场现代化，2006（32）：20-21.

[2]陈彬.基于排队论的医院体检管理系统研究[J].软件导刊，2009（9）：107-108.

[3]韩中庚.实用运筹学[M].北京:清华大学出版社，2007.

[4]丛国超，朱翼隽.批量到达的多服务台排队模型求解[J].成都信息工程学院学报，2007，22（1）：98-100.

[5]吴军.LH-SY证券营业部顾客服务系统排队模型研究[J].西安工程科技学院学报，2003，17（2）：357-361.

[6]于志清.排队论在交通工程中的应用[J].中州大学学报，2005，（1）：118-119.