Studies on Thermodynamic Properties of Some Imidazolinone Derivatives in DMF at 308.15 K
Shipra Baluja*, Asif Solanki and Nikunj Kachhadia
Department of Chemistry, Saurashtra University, Rajkot-360005, India
1 INTRODUCTION
In recent years, much effort has been made to study ultrasonic properties of liquid mixtures. However, scanty work has been done for solutions of organic compounds. In the last a few years, our groups have carried out some studies on acoustical properties of organic compounds in various solvents [1-8]. In continuation of these investigations, the present paper reports acoustical properties of imidazolinone derivatives in dimethyl formamide (DMF) over entire concentration range at 308.15 K. The results are interpreted in terms of molecular interaction occurring in the solution.
2 EXPERIMENTAL
The DMF used in the present work was of AR grade and was purified according to the standard procedure [9]. The compounds were recrystallized before use. The purity of synthesized compounds was determined by CHN analysis and is reported in Table 1.
The computation of ultrasonic and thermodynamic properties requires the measurements of ultrasonic velocity viscosity and density.
The densities (ρ) of pure solvents and their solutions were measured by using a single capillary pycnometer, made of borosil glass having a bulb capacity of 10 ml. The ultrasonic velocity (U) of pure solvents and their solutions were measured by using single crystal variable path ultrasonic interferometer operating at 2 MHz. The accuracy of density and velocity were ±0.0001 g·cm-3and ±0.001 cm·s-1respectively. The viscosity (η) of pure solvents and solutions were measured by an Ubbelohde viscometer with an accuracy of 0.05%. All the measurements were carried out at 308.15 K. The uncertainty of temperature is±0.1 K and that of concentration is 0.0001 mol·dm-3.
The experimental data of ultrasonic velocity,density and viscosity are given in Table 2.
3 THEORY
From the experimental data of density, viscosity and ultrasound velocity of pure solvent and solutions,various acoustical parameters are calculated using following standard equations.

Table 1 CHN analysis and purity of synthesized imidazolinone derivatives

Table 2 The density ρ, ultrasonic velocity U and viscosity η of imidazolinone derivatives in DMF at 308.15 K
Specific acoustical impedance:Z=Uρ
Isentropic compressibility:κs=1/(U2ρ)
Intermolecular length:Lf=KJκs1/2
whereKJis the Jacobson constant (=6.0816×104).
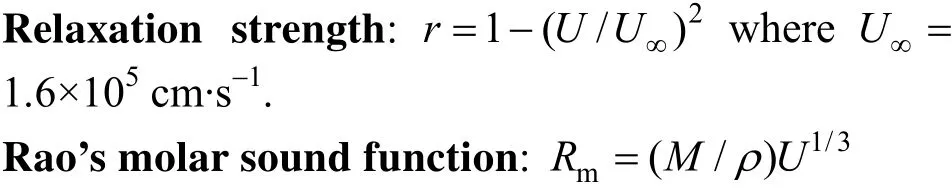
whereMis the molecular weight of solution.
van der Waal’s constant:
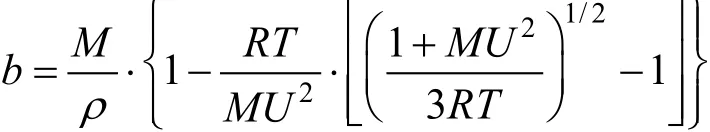
whereRis the gas constant andTis the absolute temperature.

Solvation number:
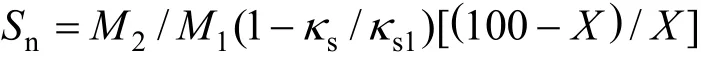
whereX(g) is the mass of solute in 100 g of the solution,M1andM2are the molecular weights, andκs1and
κsare isentropic compressibility of solvent and solute,respectively.
Apparent molar volume:
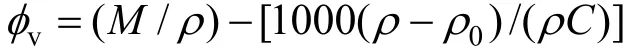
whereρandρ0are the densities of solutions and solvent, respectively, andCis the concentration of the solution in molarity.
Apparent molar compressibility:


Figure 1 Variation of ultrasonic velocity U with concentration of imidazolinone derivatives in DMF at 308.15 K
is the velocity of pure solvent.
4 RESULTS AND DISCUSSION
Table 2 shows the experimental data of pure solvents and imidazolinone derivatives at 308.15 K. Fig. 1 shows the variation of ultrasonic velocity with concentration. It is observed that ultrasonic velocityUincreases with concentration for all the compounds. The velocity depends on intermolecular free lengthLf. The velocity increases with the decreases ofLforvice versa.Table 3 shows thatLfdecreases continuously, whichsuggests that there is strong interaction between DMF and compound molecules.

Table 3 Variation of acoustical parameters with concentration of imidazolinone derivatives in DMF at 308.15 K

Table 3 (Continued)
This is further supported by isentropic compressibility κsand relaxation strength r, which are also observed to decrease with increasing concentration for all the compounds. The decrease in κswith concentration (as shown in Fig. 2) might be due to the aggregation of solvent molecules around solute molecules,indicating the presence of solute-solvent interactions.The increase of acoustical impedance Z further confirms the solute-solvent interactions in these systems(Table 3).
Properties such as Rao’s molar sound function Rm,molar compressibility W and van der Waal’s constant b are observed to increase linearly (correlation coefficient γ=0.9997-0.9999) with concentration for all the compounds. The linear variation of these acoustical properties indicates the absence of complex formation.
The internal pressure π is the results of forces of attraction and repulsion between the molecules in a solution. Table 3 shows that the internal pressure decreases as concentration increases, which indicates a decrease in cohesive forces. Although the decrease in compressibility κs, intermolecular free length Lfand relaxation strength r and the increase of velocity U and viscosity η suggest the predominance of solute-solvent interaction, the decrease in internal pressure indicates the existence of solute-solute interactions in these systems.
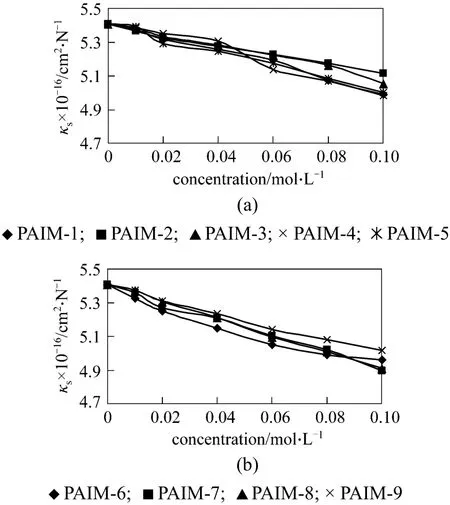
Figure 2 Variation of isentropic compressibility κswith concentration of imidazolinone derivatives in DMF at 308.15 K
The free volume Vfof solute molecule at particular temperature and pressure depends on the internal pressure of liquid in which it dissolves. The decrease in molecular association causes an increase in free volume.Thus, free volume is an inverse function of internal pressure. It is evident from Table 3 thatVfincreases with concentration for all the compounds in DMF solutions.Hence, the increase in free volume causes internal pressure to decrease, which indicates the solute-solute interactions. This suggests that both solute-solute and solute-solvent interactions exist in these systems.
Further, the apparent molar compressibilitiesφkand apparent molar volumeφvof the solutions are fitted to Gucker’s relation [10] and Masson’s equation [11]separately.

From the plot ofφkorφvversusC1/2,0kφandSkvalues or0vφandSvvalues are evaluated from the intercept and slope respectively. The isentropic compressibility of all the solutions are also fitted to the following Bachem’s relation [12]
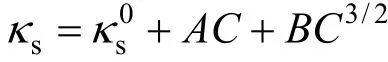
where values ofAandBare evaluated from the intercept and slope respectively. All these values of intercept and slopes are given in Table 4.
It is evident from Table 4 thatAand0kφvalues are negative for all the compounds, which indicate solute-solvent interactions. This is further confirmed by0vφvalues, which are more negative for all the compounds which suggests electrostrictive solvation of ions.Svis the measure of solute-solvent interactions.As evident from Table 4,Svvalues are higher, indicating the existence of solute-solvent interactions.

Figure 3 Variation of solvation number Sn with concentration of imidazolinone derivatives in DMF at 308.15 K

Table 4 Bachem’s constants A and B and φvo, Sv, φko and Sk of imidazolinone derivatives in DMF at 308.15 K
The interactions occurring in different solutions can also be confirmed by the solvation numberSn,which is a measure of structure forming or structure breaking tendency of solute in a solution. Fig. 3 shows that for PAIM-2 and PAIM-6, Snvalues increase with concentration. The increase in solvation number suggests an increase in structure forming tendency of compound in DMF with concentration. However, for other compounds (except PAIM-4) at low concentration (0.01 mol·L-1), Snvalues are higher, but as concentration increases it drops suddenly and then it increases further with concentration. In some cases, after increasing, it becomes almost constant. This suggests that structure forming tendency decreases as concentration increases in most of the compounds,which may be due to dipole-dipole interactions, steric hindrance. Such interactions may cause weakening between solute and solvent molecules. This weak association is further confirmed by low relative association value RA, which is almost same for some compounds (Table 3).
In PAIM-4 solutions, Snvalues decrease as concentration increases, suggesting structure breaking tendency of this compound in DMF. This compound contains bulky α-napthylamine group, which may be the reason for structure breaking tendency of PAIM-4 in DMF.
Thus, it is concluded that in DMF solution of studied compounds, both solute-solute and solute-solvent interactions exist. However, solute-solvent interactions are weak and generally decrease with the increase of concentration.
ACKNOWLEDGEMENTS
Authors are thankful to Head of Chemistry Department for providing facilities.
1 Baluja, S., Parsania, P.H., “Acoustical properties of 3-α-furylacrylic acid in protic and aprotic solvents”, Asian J. Chem., 7 (2), 417-423(1995).
2 Baluja, S., Parsania, P.H., “Studies on acoustical properties of diclofanac in dioxane-water system at 30°C”, J. Pure Appl. Ultrasonics,19, 36-42 (1997).
3 Baluja, S., Joshi, H.S., “Ultrasonic velocity studies of dimethyl phosphoryl acetyl phosphate in ethanol-water system at 30°C”, J.Ind. Chem. Soc., 76, 408-409 (1999).
4 Baluja, S., Oza, S., “Ultrasonic studies of some derivatives of sulphonamide in dimethylformamide”, Fluid Phase Equilibria, 200 (1),11-18 (2002).
5 Baluja, S., Oza, S., “Ultrasonic studies of some derivatives of 6-ethylbenzene-1,3-diol in 1,4-dioxane”, Fluid Phase Equilibria,208, 83-89 (2003).
6 Baluja, S., Shah, A., “Acoustical studies of some derivatives of 4-amino antipyrene in 1,4-dioxane and dimethylformamide at 318.15 K”, Fluid Phase Equilibria, 215 (1), 55-59 (2004).
7 Baluja, S., Pandaya, N., Kachhadia, N., Solanki, A., Inamdar, P.,“Thermodynamic and acoustical studies of binary mixtures of diethyl malonate at 308.15 K”, Phys. Chem. Liq., 43 (3), 309-316(2005).
8 Baluja, S., Shah, A., “Acoustical studies of some Schiff bases in 1,4-dioxane and DMF at 318.15 K”, Russ. J. Phy. Chem., 80, 1-5(2006).
9 Riddick, J.A., Bunger, W.B., Sakano, T., Organic Solvents: Physical Properties and Methods of Purification, 4th edition, John Wiley &Sons Inc., USA (1986).
10 Gucker, F.T., “The apparent molal heat capacity, volume and compressibility of electrolytes”, Chem. Rev., 13, 111-130 (1933).
11 Jones, G., Dole, M., “The viscosity of aqueous solutions of strong electrolytes with special reference to barium chloride”, J. Am. Chem.Soc., 51, 2950-2964 (1929).
12 Bachem, C., “Über die Kompressibilität Elektrolytischen Lösungen”,Zeit. Phys., 101, 541-577 (1936).
 Chinese Journal of Chemical Engineering2010年2期
Chinese Journal of Chemical Engineering2010年2期
- Chinese Journal of Chemical Engineering的其它文章
- Determination of Transport Properties for Dilute Gas Mixtures Involving Carbon Tetrafluoride
