基于改进遗传算法的汽轮机 DEH系统参数优化

李 娜,吕丽革

(1.华北电力大学 控制与计算机工程学院,河北 保定 071003;2.河北建投灵海发电有限责任公司,河北 秦皇岛 066001)

基于改进遗传算法的汽轮机 DEH系统参数优化

李 娜1,吕丽革2

(1.华北电力大学 控制与计算机工程学院,河北 保定 071003;2.河北建投灵海发电有限责任公司,河北 秦皇岛 066001)

在简要介绍改进遗传算法的基础上,将其应用于汽轮机数字电液调节系统的参数优化,并给出了参数优化过程。该算法有效抑制了算法早熟,提高了算法的全局搜索能力和局部搜索能力。优化结果表明,这种优化算法具有计算速度快、精度高、程序通用性强等优点,为汽轮机调节系统的参数优化提供了一种有效的方法,具有一定的参考价值。

遗传算法;数字电液调节系统;参数优化

0 引 言

汽轮机调节系统是保证机组安全稳定运行的关键设备,其性能的好坏直接影响机组的运行可靠性和经济性。机组运行工况的变化将导致调节对象运行参数和特性的变化,要保证调节系统具有良好的调节性能,需要对调节参数进行整定,以适应工况变化的要求。因此,通过对调节系统参数的优化,可以了解系统各环节参数的变化情况,便于及时发现调节系统故障以实现状态监测与故障诊断。

遗传算法是一种模拟生物进化机制的随机全局优化搜索算法,由于具有很强的全局优化能力及鲁棒性,近年来已被普遍用于生产规划、信号处理、最优控制等各个领域。本文将遗传算法引入汽轮机 DEH系统的参数优化,设计了一种快速的遗传算法,并在 MATLAB平台上进行实验。通过仿真研究验证,遗传算法是一种简单易行的优化方法,并适用于汽轮机 DEH系统参数优化,取得良好的优化效果。

1 遗传算法改进

1.1 遗传算法基本原理

遗传算法 (Genetic Algorithms)是 1962年由美国 Michigan大学的Holland教授提出的模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法。它将 “优胜劣汰,适者生存”的生物进化原理引入优化参数形成的编码串联群体中,按所选择的适配值函数并通过遗传中的复制、交叉及变异对个体进行筛选,使适配值高的个体保留下来,组成新的群体。新的群体既继承了上一代的信息,又优于上一代。这样周而复始,群体中个体适应度不断提高,直到满足一定的条件。其算法简单,可并行处理,能得到全局最优解。遗传算法的基本操作包括选择、复制、交叉、变异。遗传算法流程图如图 1。

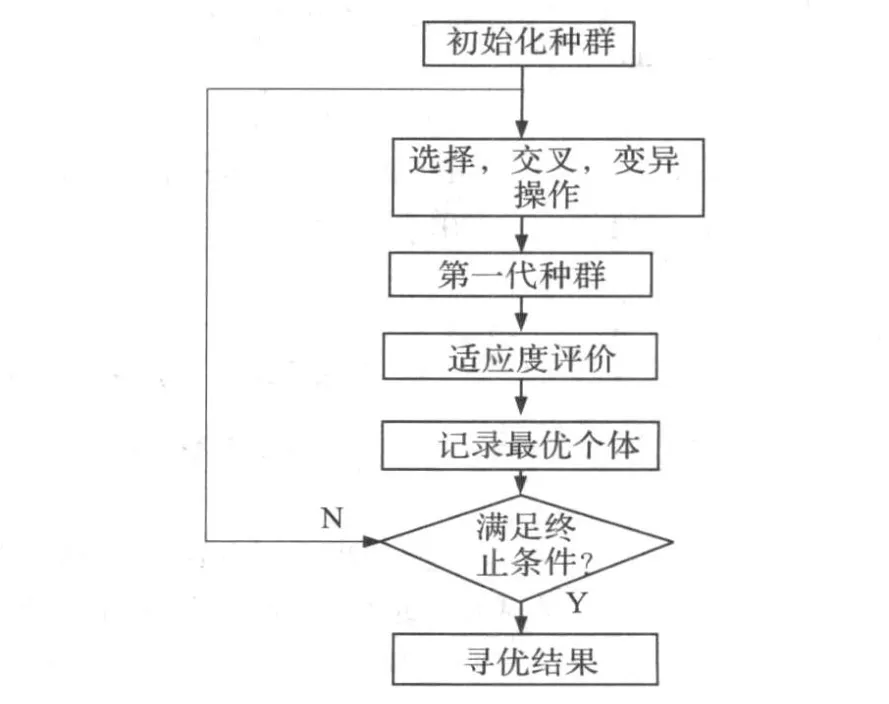
图1 遗传算法流程图Fig.1 Flow chart of GA

1.2 初始值及目标函数的选取

在优化中,初始值的选取非常重要,从不同的初始值出发所得到的优化值也不同,初始值选择不当,甚至导致优化过程发散。当优化的多个参数取值范围过大时,遗传算法的效率幅度将降低,甚至无法使用。所以根据经验,对 PID的参数取值范围进行如下限定：

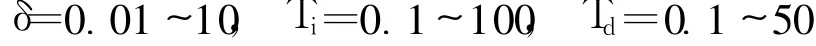
这样避免了参数范围过大,大大减小了初始寻优的盲目性,节省计算量。

对于参数优化问题,确定目标函数是寻优的前提,根据目标函数将优化问题分两类,一类是求目标函数全局最大值,另一类是求最小值[2]。

为获取满意的过渡动态特性,采用误差绝对值时间积分性能指标作为参数选择的最小目标函数,同时,为了防止控制能量过大,在目标函数中加入控制输入的平方项。选取的最优指标为：

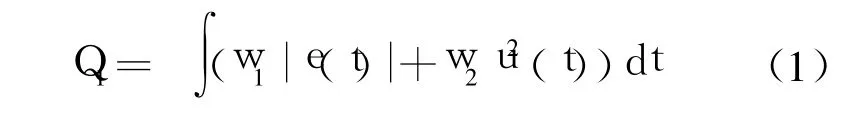
为了避免超调,可采用惩罚功能,即一旦产生超调,将超调量作为最优指标的一项,此时最优指标为：

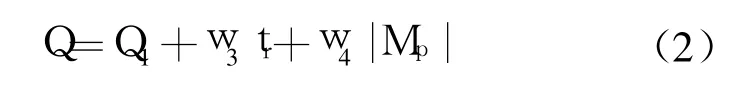
式中：e(t)为系统误差;u(t)为控制器输出;tr为上升时间; Mp是超调量。

1.3 仿真步距与仿真时间

选取原则[3]如下。

仿真步距：

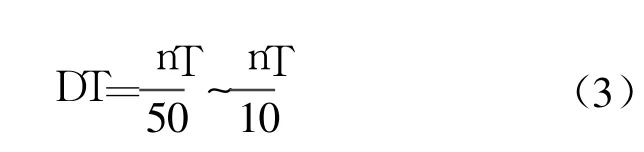
如果被控对象有若干个,则应以 nT最小的为准。

仿真时间：

以 nT最大的为准。

式中：n为被控对象传递函数的阶次;T为被控对象传递函数的时间常数。

1.4 遗传算法寻优

(1)参数选择

(2)寻优参数的编码、译码

该问题属于 3个参数寻优,采用二进制编码。兼顾到有充分的搜索空间和搜索效率,每一个参数用 code L=10位无符号二进制码表示,3个参数串接在一起构成一个样本,译码公式为：

(3)适值函数

若按照常用的比例选择算子确定个体的遗传数量,容易使适应度高的几个个体迅速占据群体,导致遗传算法的早熟现象。为此,可采用适应度尺度变换的方法,提高个体之间的竞争。在初始阶段,缩小各个体适应度的差距,限制复制数量,在后期阶段,对适应度进行适当放大。

适值函数实际上就是目标函数的另一种表示形式。由于遗传操作是根据适值大小进行的,且适值是非负的,而目标函数的优化方向应对应适值增加的方向,所以将目标函数 Q转换成适值函数 F,本文选用下式作为适值函数：

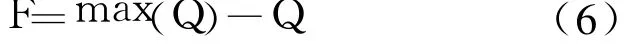
(4)选择、交叉、变异算子对种群 E(t)进行操作,产生下一代种群 E(t+1)。

在选择过程中是对适应度最高的个体,不进行遗传操作而直接复制到下一代,该方法可以保证某一代的最优解不被破坏。

基本遗传算法的交叉操作,由于其搜索空间较小,有可能会陷入局部最优,丧失寻找最优解的可能。本文将群体等分组,若该组对应的随机数小于交叉概率,则对每组中的任意两个个体均进行一次非均匀算术交叉,再对这部分个体进行适应度值排序,按照从大到小的顺序依次取前个个体去替代原来的父个体。若该组对应的随机数大于交叉概率,则不进行交叉操作。采取该方法能够有效扩大搜索空间,提高收敛速度。

变异的本质是挖掘群体中个体的多样性,同时提高算法的局部随机搜索能力。变异步长的选择比较困难,为保证维持群体的多样性,防止出现早熟现象,随着进化代数的增加,变异步长逐渐减小,这有利于提高遗传算法的局部搜索能力。

2 汽轮机电液调节系统原理

在电液调节系统中,为了适应中间再热式汽轮机的特点,提高其负荷适应能力,通常采用功率—频率电液调节系统[4],如图 2所示。

图2 汽轮机数字式电液调节系统Fig.2 Turbine DEH control system

汽轮机共有 4个典型工况：转速调节工况(机组启动工况);功率—功率调节工况 (并网运行工况);功率调节工况 (实际是并网运行工况的特例);甩负荷工况。

虽然汽轮发电机组的电液调节系统存在不同的运行工况,但是对于参数优化来说,优化方法是一定的,并不随着工况的变化而变化,因此,在优化计算中,仅以典型的并网运行调节工况为例进行优化研究与计算说明。

机组并网运行参加一次调频时,汽轮机功频电液调节系统投入运行。当现场的汽轮发电机组采用功率—频率调节时,电网的容量都是可以近似认为无穷大的,并且电网的频率变化波动非常的小,可以近似认为电网的频率是稳定的。此时的电液调节系统的模型可以近似地与汽轮发电机组采用功率调节时的相同,这时候模型中调节系统的转速回路不起作用。因此,这里将机组的这两种运行方式放在一起进行讨论与分析。简化的机组功率—频率调节工况的模型如图 3。

图3 并网后简化功频调节工况下框图Fig.3 Frequency-regu lation condition a fter breaker closed

3 参数优化的仿真研究

在数字电液调节系统中,PID调节器的参数由运行人员根据机组的运行工况进行调整或者由自适应控制系统根据机组的状态进行调整。由于此系统的响应特性对 PID调节器参数的变化非常敏感,PID调节器参数的微小变化将使得系统的响应特性有很大的变化,结合遗传算法的优势,将其应用在汽轮机功频调节系统的 PID参数优化中,并进行分析。

针对功率—功率调节工况,首先功率给定信号 10 MW的阶跃输入,结合对象特性,由 GA方法进行参数寻优,PID参数优化结果如表 1所示。

通过遗传算法进行参数优化的输出曲线以及代价函数值 J的优化结果见图 4,图 5。

从程序编写过程和输出曲线总结出改进遗传算法的优势性：

表 1 功频调节工况下PID参数优化结果Tab.1 Param eter opitim azation results for PID under frequency-reyu lation condition

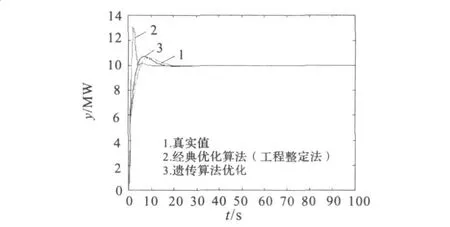
图4 不同方法参数优化的输出曲线对比Fig.4 Output curve in different w ays to optim ization

图5 遗传算法代价函数值的优化Fig.5 Optim ization of cost function based on GA

(1)经典参数整定计算量大,遗传算法操作方便、速度快,只需要通过字串进行简单地复制、交叉、变异,便可以达到寻优,避免了大量的计算,具有操作方便、速度快的特性,改进的遗传算法中对寻优参数的范围限定使的在遗传到 30代左右的时候已经达到最优。

(2)输出曲线说明遗传算法具有良好的寻优特性。改进遗传算法具有很强的寻优能力,其系统输出响应曲线上升速度快、超调量小 (基本无超调)、达到稳定的时间短。

4 结 论

基于改进遗传算法的参数优化具有计算速度快、优化结果准确可靠等优点,优化具有极强的鲁棒性,是实现系统参数优化的一种有效的新方法。针对汽轮机功频调节系统的快速性,遗传算法表现出了它的优势性,但是对于 GA的进一步应用,尚有以下问题需要研究并解决,比如如何选择合适的参数加速优化过程的收敛,如何解决计算的盲目性及冗余度问题等。

[1]刘金琨.先进PID及其 MATLAB仿真 [M].北京：电力工业出版社,2003.130-135.

[2]刘长良,于希宁.基于遗传算法的火电厂热工过程模型辨识[J].中国电机工程学报,2003,23(3)：170-174.

Liu Changliang,Yu Xining. Midel identification of power plant thermal process based on genetic algorithm[J].Proceedings of the CSEE.2003,23(3)：170-174.

[3]韩璞.控制系统数字仿真技术 [M].北京：中国电力出版社,2007.48-51.

[4]李涌.汽轮机电液调节系统建模及其参数辨识 [D].杭州：浙江大学,2005.

Li Yong. Modeling and parameter identification of turbine electro-hydraulic control system[D].Hangzhou：Zhejiang University,2005.

[5]马进,王兵树.基于遗传算法的热力设备机理模型参数优化方法研究 [J].华北电力大学学报,2008,35(5)：73-77.

Ma Jin,Wang Bingshu.Study on parameter optimization using genetic algorithm for mechanism model of thermal thermal equipment[J].Journal of North China Electric Power University,2008,35(5)：73-77.

[6]叶乐,赵文杰.遗传算法在热工对象辨识中的应用[J].电力科学与工程,2009,25(4)：47-49,58.

Ye le,Zhao Wenjie.Application of genetic algorithm in model indentification of thermal process[J].Electric Power Science and Engineering,2009,25(4)：47-49,58.

Parameter Optimization for Turbine DEH Control System Based on Im proved Genetic A lgorithm

LiNa1,Lu Lige2
(1.Schoolof Control and Computer Engineering,North China Electric Power University,Baoding 071003,China;2.Hebei Construction Investment LinghaiPower Co.,Ltd.,Qinhuangdao 066001,China)

Improved Genetic Algorithm(GA)is used for parameter optimization of turbine Digital Electrical Hydrau lic(DEH)governing system after introduction.One improved genetic was put forward to restrain the premature convergence effectively and increase the global and local search capability.The optimization results showed that such method with GA has theadvantages of fast computation,high parameter optimization precision,and better program generality.It provided a new way for parameter optim ization of steam turbine governing system.

genetic algorithm;DEH control system;parameter optim ization

TK 321

A

2009-12-22。

李娜 (1985-),女,硕士研究生,研究方向为智能算法在电厂中的应用,E-mail：lina144@163.com。