基于投影寻踪动态聚类模型的边坡稳定性评价

张鹏洲,倪长健

(成都信息工程学院大气科学系,成都 610041)

1 引 言

投影寻踪就是将高维数据向低维空间投影,通过分析低维空间的投影特性来研究高维数据的特征,是处理多因素复杂问题的统计方法[1]。投影寻踪聚类模型则是依据投影寻踪思想建立的聚类分析模型,它已在诸多领域获得了广泛的应用[2～9]。通过分析,投影寻踪聚类模型在实际聚类分析应用中还存在有待深入研究和改进的问题,主要体现在以下两方面：

(1)投影寻踪聚类模型中的唯一参数——密度窗宽取值问题。研究表明,密度窗宽的不同取值对聚类结果有重要影响[3],可到目前为止其取值大小还是通过经验或试算确定,缺乏理论依据。采用较普遍的就是 Friedman和 Tukey建议的密度窗宽取全部样本投影特征值方差的 10%。其次,文献 [4]给出了密度窗宽取值的经验公式,并建议可将样本聚类指标个数作为其实际取值,然而,这也是依据有限实验的统计结果,事实上,当密度窗宽取值太大时,模型中的投影指标实质上就只是体现了样本投影特征值的方差。因此,关于密度窗宽参数的合理取值问题还有待深入研究。

(2)投影寻踪聚类模型运算结果的再分析问题。对于没有分类标准参照的聚类问题,投影寻踪聚类模型只能得到基于投影特征值大小的样本排序,并不能直接提供明确的聚类结果。对于线性投影寻踪聚类模型,传统的处理方法也是目前普遍采用的方法就是绘制投影特征值散布图[5],分析人员凭肉眼根据投影特征值散布情况给出样本聚类结果。由于没有定量的聚类依据,有时就难以划定明确的聚类界限,实际应用中不可避免地会受到人为因素的影响。尽管进行了一些改进[6],但是投影寻踪聚类模型在进行聚类分析时仍不能直接提供明确的聚类结果,不便于推广应用。

针对投影寻踪聚类模型的上述问题,我们引入动态聚类方法[7],首次以动态聚类原则构建投影指标,从而建立了基于投影寻踪原理的动态聚类模型,即投影寻踪动态聚类 (projection pursuit dynamic cluster,简称 PPDC)模型。本文将详细介绍投影寻踪动态聚类模型的实现过程,并在边坡稳定性评价中进行了实际应用,最后和已有的应用结果作了对比分析。

2 投影寻踪动态聚类模型

步骤 1：数据无量纲化。由于各评价指标的量纲不尽相同,为了消除量纲效应,在建模之前对各指标数据进行无量纲化处理,对于越大越优的指标对于越小越优的指标分别为第 j个指标的样本最大值和最小值。

步骤 2：线性投影。投影就是从不同角度观察数据,寻找能够最大程度地反映数据特征和最能充分挖掘数据信息的最佳观察角度即最优投影方向。高维数据信息通过投影转化到低维空间,不但形象直观,而且便于运用常规方法进行分析处理,本文采用线性投影,即将高维数据投影到线性空间。设为 m维单位投影方向向量,其分量为 a1,a2,…,am,则 xij的投影特征值 zi可表示为：

步骤 3：构造投影指标。这是投影寻踪动态聚类模型建立的关键,是高维数据向低维空间投影聚类所遵循的原则,是寻找最优投影方向的依据,只有构造合理的投影指标才能取得合理的聚类结果。本文首次应用动态聚类方法[7]来构造投影寻踪动态聚类模型的投影指标。

整个样本的投影特征值序列组成的集合记为：Ω={z1,z2,…,zn},采用动态聚类法将其聚为p(p≤n)类,Θh(h=1,2,…,p)为由属于 h类的所有样本投影特征值构成的集合,定义 s(zi, zj)为任意两投影特征值间的绝对值距离。

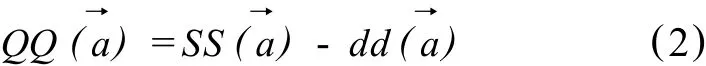
投影寻踪动态聚类模型的投影指标定义为投影分散度与类内聚集度之差,表示类间所有样本投影特征值的距离之和,对其求解就是寻求某一投影方向满足 ss(a)-dd(a)取得最大值,显然,投影分散度越大或类内聚集度越小,则投影指标越大。当取得最大值时,就实现了类间样本尽量散开、类内样本尽量集中的聚类目的,此即为投影寻踪聚类的思想。

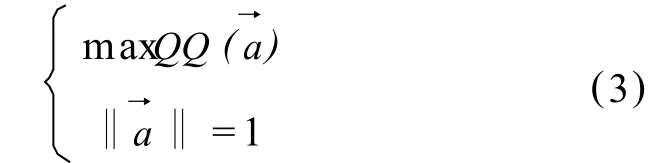
本文采用遗传算法求解[2]。

3 应用实例

边坡稳定性问题一直是岩土工程的一个重要研究内容,边坡稳定性的评价与预测是边坡工程研究的根本问题,也是边坡研究中最难和最迫切的课题之一,而边坡稳定性评价结果的正确与否直接关系到边坡工程的成败,具有十分重要的意义。边坡是由漫长的地质作用造成的,地质环境的复杂性和影响边坡稳定性因素 (如斜坡的外形、岩性、构造、水、地震和人为因素等)的不确定性,使边坡稳定性问题表现为多因素、多层次和多阶段的复杂动态非线性系统,故边坡稳定性评价是一项复杂的综合评价过程。针对影响边坡稳定性的诸多因素的不完整性和不确定性,研究人员先后提出了一些新的边坡稳定性评价方法,如模糊综合评价方法、灰色聚类评价方法、可靠度评价方法、系统聚类评价方法以及神经网络评价方法等等。这些评价方法的提出从不同侧面反映了影响边坡稳定性的不确定性质,但不论是确定性分析还是不确定性方法其用于边坡稳定性评价的准确性与实际情况仍有差距 ,另一方面,上述方法往往还存在评价过程中诸如权重确定没有统一的理论和计算公式、神经网络结构试算确定、评价过程相对复杂等不足。本文在边坡稳定性评价的投影寻踪聚类模型的基础上[8],运用投影寻踪动态聚类模型对此问题进行了进一步研究。同文献 [8],所选取的指标体系包括高差(1)、坡角 (2)、洪水位与滑坡剪出口高程关系(3)、滑体面积 (4)、滑体透水性 (5)、暴雨强度 (6)、变形破坏迹象 (7)、物质结构 (8)活动面产状变化情况 (9)、滑带强度 (10)、剪出口产状 (11)、人类活动情况 (12)、岩石层位组成(13)、岩石倾角 (14)等 14个指标,这些指标的样本数据见下表。按 PPDC法的计算步骤,其中m =14,n=12,p=5,得到最优投影方向向量为 a＊=(0.0224,0.3731,0.0241,0.2214,0.3308, 0.3003,0.3031,0.3570,0.2819,0.2345,0.2948, 0.4081,0.0625,0.0009),把 a＊代入式 (1)后即得到各典型滑坡体的投影值 z＊(i),结果见下表。投影特征值 z＊(i)越大,表示滑坡体的不稳定水平越大。

由下表可知,黄腊石 I、新滩、天宝聚为第 I类,为稳态 A级;云阳西城单独聚为第Ⅱ类,为稳态B级;宝塔、黄腊石Ⅱ、流来观聚为第Ⅲ类,为稳态 C级;白衣庵、向家湾聚为第Ⅳ类,为稳态D级;百换坪、范家坪、旧县坪聚为第 V类,为稳态 E级。A、B、C、D为不稳定状态,稳态分级标准祥见文献 [9]。此聚类结果与神经网络方法结果[9]一致,说明投影寻踪动态聚类模型运算可靠,结果合理。

表 边坡的分类指标样本数据及其投影值Tab. The indexes values of slope samples data and their projection values

应用分析表明,投影寻踪动态聚类模型具有如 下特点： (1)在整个运算过程中,仅仅需要预先给定样本的聚类数,而不需要人为给定其他任何参数,避免了投影寻踪模型中密度窗宽确定的人为任意性,因此,投影寻踪动态聚类模型具有普适性,便于实际应用推广。 (2)与投影寻踪聚类模型相比较,投影寻踪动态聚类模型不但可以直接得到投影特征值和最优投影方向向量,而且可以得到明确的聚类结果,避免了结果的经验判定。

4 结 论

投影寻踪动态聚类模型是处理多因素聚类问题的一种新的分析方法,它依据投影寻踪聚类的建模思想,应用动态聚类方法构造投影指标,有效地避免了投影寻踪聚类模型的不足：一方面,投影寻踪动态聚类模型在运算过程中不存在需要人为给定的参数;另一方面,投影寻踪动态聚类模型是投影寻踪原理与动态聚类方法的有机结合,可以直接输出聚类结果,避免了结果的再分析。边坡稳定性评价的实际应用表明,投影寻踪动态聚类模型切实可行,具有稳定性好、客观性强、分类结果明确、操作简便等优点,便于推广应用,为多因素样本聚类分析开辟了一条新途径。

[1] Friedman J H,Tukey J W.A projection pursuit algorithm for exploratory data analysis[J].IEEE Trans on Computer,1974,C-23 (9)：881-890.

[2] 张欣莉,丁 晶,李祚泳,等.投影寻踪新算法在水质评价模型中的应用[J].中国环境科学,2000,20(2)：187-189.

[3] 张欣莉,任仕泉,罗 利.企业竞争力评价的投影寻踪模型[J].数理统计与管理,2005,25(4)：53-55,117.

[4] 王顺久,张欣莉,丁 晶,侯 玉.投影寻踪聚类模型及其应用[J].长江科学院院报,2002,19(6)：53-55,61.

[5] 王顺久,侯 玉,张欣莉,丁 晶.流域水资源承载能力的综合评价方法[J].水利学报,2003,34(1)：88-92.

[6] 金菊良,张欣莉,丁 晶.评估洪水灾情等级的投影寻踪模型[J].系统工程理论与实践,2002,22(2)：140-144.

[7] 任若恩,王惠文.多元统计数据分析—理论、方法、实例[M].北京：国防工业出版社,1999.76-80.

[8] 汪明武,金菊良.投影寻踪聚类方法在边坡稳定性分析中的应用[J].岩土工程学报,2002,24(5)：619-621.

[9] 崔政权,李 宁.边坡工程—理论与实践最新发展[M].南京：南京大学出版社,2000.