海底隧道预注浆加固效果检查与评价

汪 磊,李 涛,王全胜

(1.上海工程技术大学城轨学院,上海 201620;2.北京交通大学土建学院,北京 100044;3.中铁隧道科研所,河南洛阳 471009)

注浆技术自从发明以来,已经广泛地应用于封堵涌水和改良地层,在基础建设的各个方面起到了良好的作用。而在海底隧道的修建中,由于环境的特殊性,裂隙岩体和无限量的海水补给使得隧道的安全施工更加特殊,隧道突涌水破坏或围岩失稳都会带来不可挽回的后果,因此，对于不良地质段隧道的施工往往采用预注浆对围岩进行超前加固,但目前预注浆效果检查技术很不规范,尚无完善的标准可以借鉴,继而导致了一些注浆工作完成后无法正确评价,从而影响了注浆工程取得良好的效果。本文以青岛胶州湾海底隧道断层F4-4第一循环预注浆为背景,针对海底不良地质段隧道预注浆效果进行研究。利用理论公式法、数值法和现场实测的方法对涌水量进行计算和测定,比较它们之间的关系,分析其中的规律,得出海底隧道的实际注浆效果。

1 工程概况

青岛胶州湾海底隧道是我国大陆第二条海底隧道,隧道南接黄岛区的薛家岛,北连青岛团岛,下穿胶州湾湾口海域,隧道全长6 170 m,其中海域段长3 950 m。隧道采用双向双洞六车道,中间设服务隧道,隧道主要采用钻爆法施工。根据前期工程地质勘探的结果,隧道海域段基岩受构造运动影响较严重,破碎岩体及抗风化能力较低的辉绿岩脉较发育,对水敏感的Ⅳ～Ⅴ级围岩所占比例较大,其中,隧道主洞II～III级围岩约占55.7%,IV级围岩约占38.1%,V级围岩约占6.2%。隧道顶部25 m内岩体中的地下水活动痕迹普遍较明显,隧道开挖时的爆破震动和围岩松弛都可能使其透水性加剧,埋深不足25 m的海域段占了相当大的比例。

2 涌水量计算

2.1 涌水量理论计算

2.1.1 理论计算地质模型

断层F4-4位于隧道YK6+915～YK6+961段,长46 m,高潮时水深27～30 m；海床呈缓坡状。海底覆盖层较薄,一般为2～3 m,主要为砂砾,局部沉积有淤泥。隧道拱顶覆盖层24～26 m。基岩以含晶屑火山角砾凝灰岩为主,局部夹凝灰岩、并有较多辉绿岩脉、石英正长岩脉侵入。断层F4-4为北西向破碎带,带内岩体为碎裂—镶嵌碎裂结构,裂隙以密闭型为主,少数为微张型,裂隙面浸染迹象不甚明显；围岩在松弛变形时抗渗性能易恶化,还可能发生渗透变形破坏。注浆施工地段为断层F4-4,相对位置如图1所示。

考察相关地质资料,断层F4-4为弱风化岩体受风化裂隙影响,具有弱～中等透水性,综合渗透等级为中等透水。具体各层渗透系数见表1。

表1 海域岩土体渗透系数统计综合成果

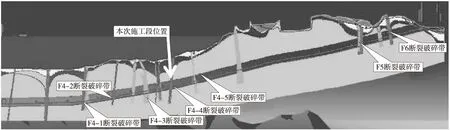
图1 断层F4-4相对位置示意

为了使所研究的海域段隧道穿越断层F4-4更具有指导意义,具体计算位置为断层F4-4的两端和中间,即为YK6+915、YK6+938和YK6+961。

2.1.2 理论计算概化模型

根据地质模型,建立涌水量的理论计算模型。如图2所示。当隧道围岩含有两种以上的含水层介质时,其渗透系数按下式进行等效化处理

(1)

式中，n、Mi、Ki分别为渗透性分层的数目、第i层的厚度和渗透系数。图2中H为含水层中原始静水位至隧道等价圆中心的距离，m；H0为含水体厚度，m；r为隧道洞身横断面的等价圆半径，m；d为隧道洞身横断面的等价圆直径，m。

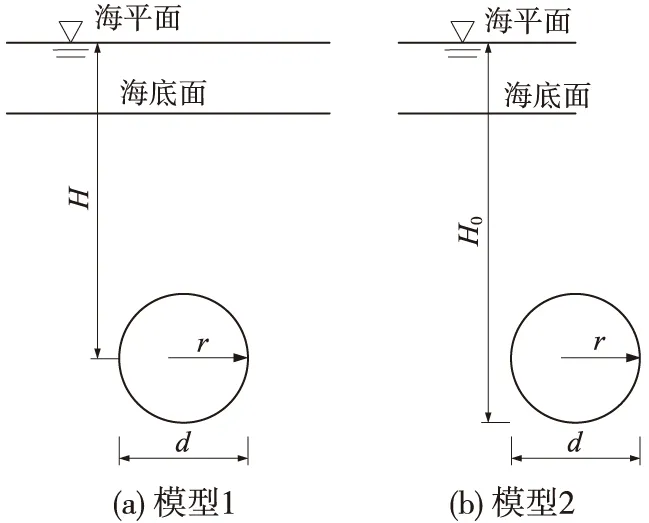
图2 涌水量计算概化模型示意

2.1.3 理论计算公式及结果

海底隧道位于半无限含水层中,地下水直接接受海水的定水头入渗补给,施工前期的最大涌水量与施工中的经常涌水量基本一致。其最大涌水量的计算公式如下。

(1)大岛志洋公式(模型1)

(2)

式中，q0为单位长度可能最大涌水量，m3/d·m；K为岩层渗透系数；H为含水层中原始静水位至隧道等价圆中心的距离，m；r为隧道洞身横断面的等价圆半径，m；d为隧道洞身横断面的等价圆直径，m；m为转换系数,一般取0.86。

(2)铁路规范古德曼经验式(模型1)

(3)

式中，q0为单位长度最大涌水量，m3/d·m；K为渗透系数，m/d；H为静止水位至洞身横断面等价圆中心的距离，m；d为隧道洞身横断面等价圆直径，m。

(3)铁路规范经验式(模型2)

q0=0.025 5+1.922 4K·H

(4)

式中，q0为单位最大涌水量，m3/d·m；K为渗透系数，m/d；H为含水体厚度，m。

(4)注浆后涌水量计算公式

(5)

式中，Q为单位最大涌水量，m3/d·m；Ki为注浆区域渗透系数，m/d；K为岩体渗透系数，m/d；h为含水层中原始静水位至隧道等价圆中心的距离，m；R为隧道等效半径，m；t为注浆加固圈厚，m。

利用如上4个公式计算结果分别如表2～表5所示。

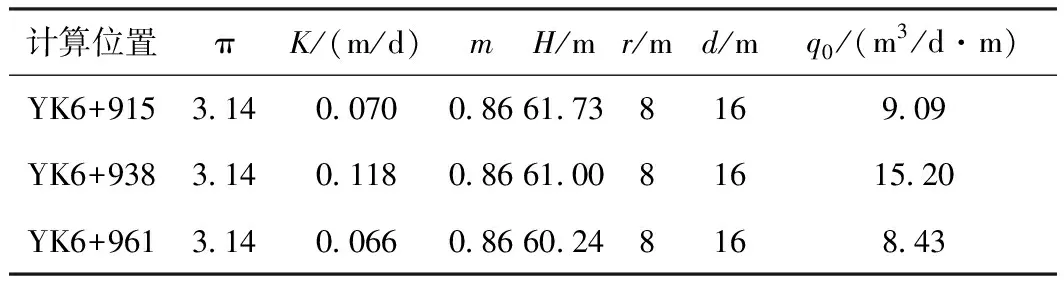
表2 海域隧道(右洞)涌水量计算(大岛洋志公式)

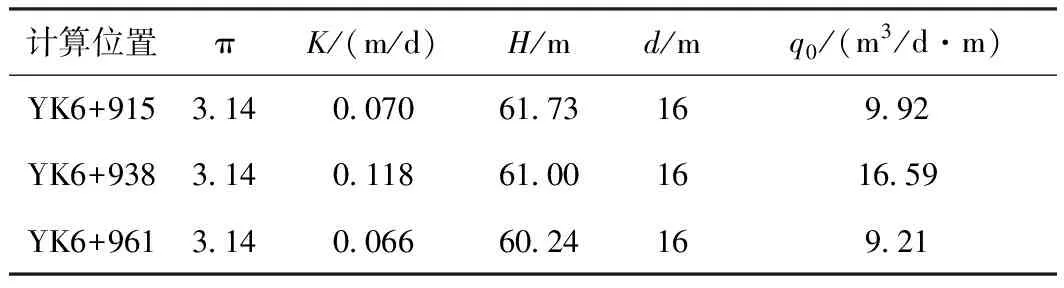
表3 海域隧道(右洞)涌水量计算(铁路规范古德曼经验式)

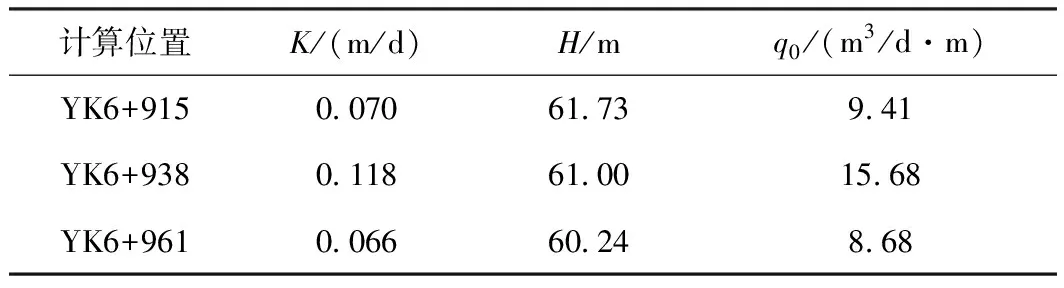
表4 海域隧道(右洞)涌水量计算(铁路规范经验式)

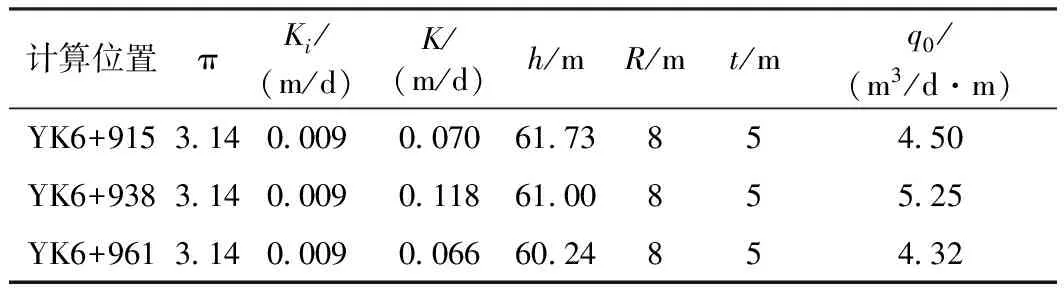
表5 海域隧道(右洞)涌水量计算(注浆后)

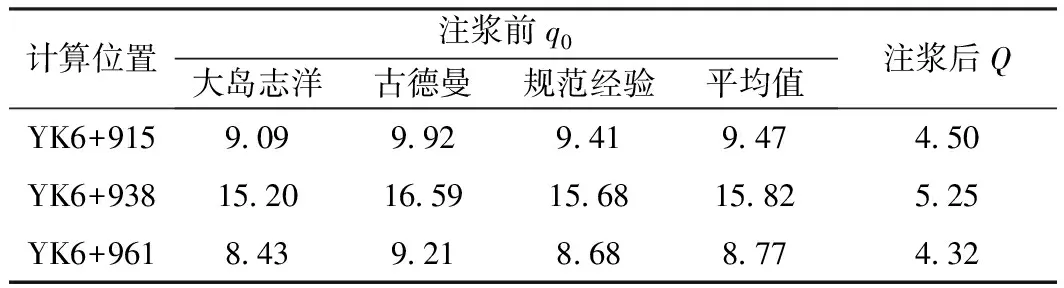
表6 海域隧道(右洞)最大涌水量对比 m3/d·m

分析表6,在断层F4-4地段隧道右洞沿线的涌水量计算时用不同的公式计算所得结果有所不同,用大岛洋志公式计算的涌水量最小,铁路规范古德曼经验式计算的涌水量最大,铁路规范经验式计算的涌水量居中。不过总的来说,三者结果相差不大,断面YK6+915涌水量大约为9.47 m3/d·m；断面YK6+938涌水量大约为15.82 m3/d·m；断面YK6+961涌水量大约为8.77 m3/d·m。

根据注浆后试验测得,注浆体的渗透系数大约为1.0×10-5cm/s,利用公式(5)可得注浆后的涌水量结果如表5所示,并将其与注浆前的涌水量进行比较可知,通过注浆后隧道涌水量明显降低,由于在过同一个断层F4-4的时候使用的是同样的注浆结束标准,所以注浆结束后注浆体的渗透系数相似,进而注浆后各个断面上的涌水量也相近。

2.2 涌水量数值计算

2.2.1 数值计算概化模型

为了与理论公式及经验公式的计算结果进行对比,数值法计算仍取在断层F4-4范围即隧道YK6+915～YK6+961段内的两端和中间的3个断面进行模拟计算。具体位置分别为YK6+915、YK6+938和YK6+961,其中在断面YK6+915和断面YK6+961计算的涌水量代表断层两头处隧道内的涌水量情况,而在断面YK6+938所计算的涌水量代表断层中间处的涌水量情况。另外,不考虑双洞渗流效应,仅考虑右线隧道断面内的涌水量情况。计算剖面1见图3(其他2个剖面类似),其中水平向取200 m,竖向取100 m(不包括海水部分)。

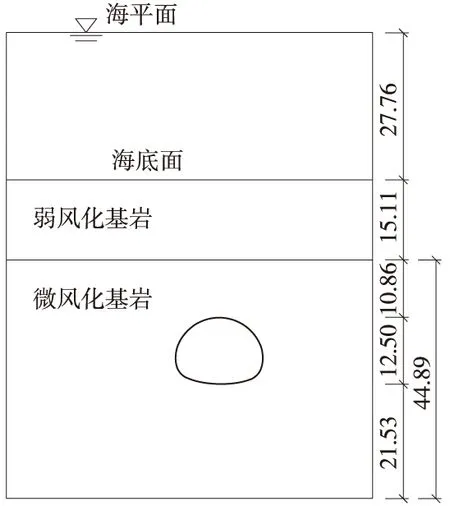
图3 剖面1(YK6+915)(单位：m)

YK6+915、YK6+938和YK6+961 3个剖面均为海域剖面,左右两侧及顶部均有水源补给,而且认为所选计算范围足够大,因此可以视为定水头边界,水头值等于海平面所对应的位置高程(即水头),为承压渗流场。另外,由于隧道处岩体的渗透性较差,地下水以渗出的形式涌出,因此隧道内侧可作为第一类边界(自由渗出面)加以模拟；隧道底部边界以下地下水呈水平渗流状态,对隧道涌水量影响较小,视为第二类边界条件(零流量边界)。

2.2.2 数值计算理论基础

单位厚度的隧道涌水量理论计算公式如下

(6)

式中,L为隧道周边轮廓；n为隧道壁法线方向；其他参数意义同前。

实际计算中,作如下简化：用隧道壁4个特征点(顶点、左侧点、底点、右侧点)(图4)位置处的单宽流量的平均值代表整个隧道壁的单宽流量Q0,Q0与隧道周长L的乘积即为单位厚度隧道涌水量。

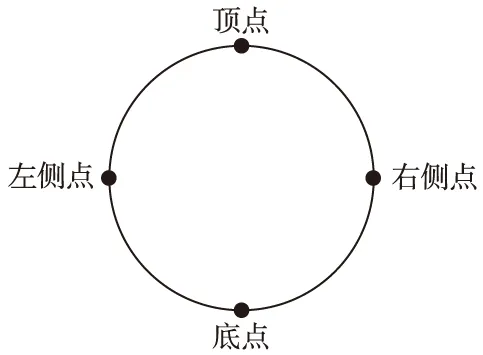
图4 隧道涌水量计算点示意

2.2.3 数值计算分析

为了分析考虑隧道穿越F4-4断层时预注浆加固前后涌水量的比较,考虑了3种工况进行分析：

(1)无预注浆加固时,考虑渗流场作用下隧道涌水量的计算；

(2)采用不同的预注浆加固圈厚度(分别取3、4、5、6、7 m和8 m)时,考虑渗流场作用下隧道涌水量的计算,其中设围岩渗透系数Kr与注浆圈渗透系数Kg,令Kr/Kg=2、Kr/Kg=5和Kr/Kg=10；

(3)采用设计注浆加固圈厚度为5 m,令Kr/Kg=2、Kr/Kg=3、Kr/Kg=4、Kr/Kg=5、Kr/Kg=6、Kr/Kg=7、Kr/Kg=8、Kr/Kg=9和Kr/Kg=10时,考虑渗流场作用下隧道涌水量的计算。

胶州湾海底隧道预注浆加固圈的设计厚度为5 m,但对于不同的注浆剖面所取得的注浆效果也不同,主要由于所注围岩的地质特征不同,进而表现为隧道开挖时的涌水量不同。如图5为当注浆加固圈厚度为5 m时,采用不同的注浆圈渗透系数可以计算出不同的日涌水量。对于剖面1和剖面3当Kr/Kg>5后,隧道开挖涌水量的计算结果减少变缓；对于剖面2当Kr/Kg>7后就会出现隧道开挖涌水量的计算结果减少变缓的现象。

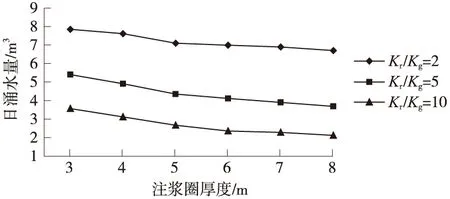
图5 隧道开挖涌水量随注浆圈渗透系数的变化

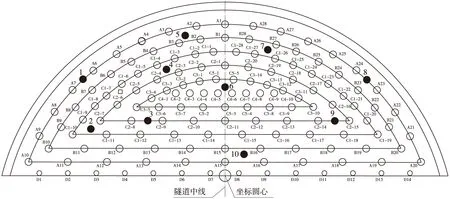
图7 检查孔布置

当所取注浆圈的渗透系数相同而注浆圈厚度不同时,计算所得隧道开挖日涌水量也不相同。如图6分别为剖面1(其他2个剖面类似)在隧道开挖涌水量随注浆圈厚度的变化情况,计算中分别考虑了Kr/Kg=2、Kr/Kg=5和Kr/Kg=10 3种情况。从图中可以看出，这3种情况下隧道开挖涌水量随注浆圈厚度变化的规律是相似的,并且当注浆圈厚度大于5 m后,隧道开挖日涌水量的变化逐渐趋缓并最终趋向于稳定。

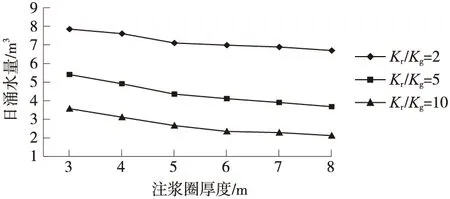
图6 剖面1隧道开挖涌水量随注浆圈厚度的变化

同时,当注浆圈从3 m增加到8 m的过程中在各个渗透系数确定的情况下,隧道开挖日涌水量的变化值也是几乎相同的。这就可以说明对于同一渗透系数,注浆圈厚度的改变对隧道开挖日涌水量的控制是有限的,所以对于一定的隧道围岩地质状况,当注浆材料、注浆工艺等确定时,必需注意控制注浆效果,避免浪费。

3 海底隧道预注浆检查

此循环总注浆量为1 285.4 m3,总进尺为30 m,平均每延米注浆量为42.85 m3。单孔最大注浆量为0.51 m3/m,主要集中在隧道开挖面的上部和左侧,此处裂隙较大,出水量较大；右侧孔(地质情况较好)出现最小注浆量0.2 m3/m。

注浆分多次扫孔完成,注浆主要是填充裂隙加固岩层。拱顶部位是注浆的关键,从地质探孔和注浆钻孔情况分析,拱顶正上方5 m,而这一位置恰好处于B续孔端部,为注浆加固之薄弱环节。拱顶A5、A6、B3、C1、C3等孔注浆量也较大,达到0.4～0.51 m3/m,在这4个孔中扫孔至7 m开始有较大出水量,在第二次补充注浆扫孔后无水或水量很小,但注浆量依然很大,注浆压力很低(1 MPa左右),上升缓慢甚至注浆量达到设计值而压力无法达到设计值。通过反复分析扫孔和注浆过程,在拱顶正上方偏左1～3 m,深度为17～20 m位置处有结构面,存在较大的裂隙,通过注浆已完全封堵了此裂隙。

此循环注浆为挤密注浆,注浆过程控制采用“控压限量”的方法,注浆压力限制在3～4 MPa内,主要以控制注浆压力及流量作为单孔每循环注浆结束标准。

3.1 注浆检验孔布置

注浆效果检查采用钻检查孔法,根据注浆状况,选择注浆范围存在薄弱环节的注浆部位布设检查孔,检查孔布置如图7所示。

3.2 实测涌水量统计(表7)

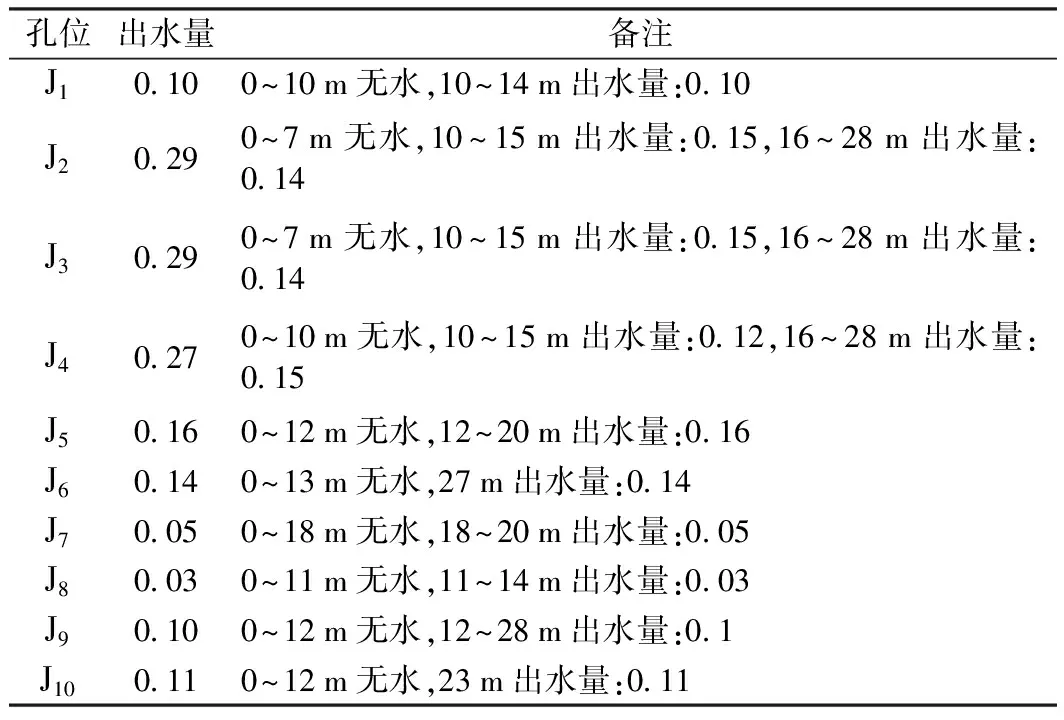
表7 检查孔出水量汇总 L/min

分析如上各孔的出水量,总共出水量为1.49 L/min。其中,J2、J3和J4出水量较大,J7、J8出水量较小,可以说明隧道左侧裂隙较发育,出水量较大,这和前面整个断面内的注浆量分布是相对应的。为了进一步研究出水量在注浆前后的分布规律，下面将综合公式法和数值法对涌水量进行计算。

4 涌水量计算比较及分析

4.1 无注浆情况下隧道开挖涌水量计算比较

在无注浆情况下,利用公式法和数值法的隧道开挖涌水量计算结果如表8所示。

表8 无注浆情况下隧道开挖涌水量计算结果 m3/d

通过分析表8可以发现，在剖面1和剖面3利用公式法计算的结果较数值法小一些,而在剖面2正好相反。分析两种计算方法,对于公式法,它有很多的不足,比如说：只能考虑围岩渗透系数为各向同性；只能对圆形洞室进行求解；大部分公式只是对毛洞进行研究，不能考虑注浆、衬砌结构等的影响；不能考虑渗流场和应力场等的耦合作用。而对于数值法,在求解边界条件复杂、本构关系复杂的问题上有很大的优势,但它的计算结果有很大的随意性,仍然有它的不足,其中涌水量的计算结果受所取渗透系数、计算模型大小、网格划分质量等条件影响很大。另外,就计算的3个剖面而言,3个剖面所对应的地质情况不相同,计算所得渗透系数也不同,其中在数值法计算中隧道围岩的渗透系数是按公式等效后选用的,而在这个等效化公式中涉及到了模型尺寸,所以即使对于同一计算剖面,而选用不同的计算模型就会得出不同的等效化渗透系数,进而计算出不同的涌水量。即而会出现剖面1和剖面3利用公式法计算的结果较数值法小一些,而剖面2正好相反的情况。

4.2 注浆情况下隧道开挖涌水量计算比较

比较公式法和数值法在注浆后的隧道开挖涌水量见表9,一方面注浆后的比较结果和注浆前的比较结果是一样的；另一方面,剖面1和剖面2的计算结果相似的。所以在实地注浆的时候,注浆设计时可以将Kr/Kg=5所对应的注浆量作为实际设计值进行参考,而剖面2的注浆量Kr/Kg=5所对应的注浆量及注浆压力基础之上应该有所提高,才能充分达到预期的注浆效果。

表9 注浆后隧道开挖涌水量计算结果 m3/d

4.3 与实测数据的比较

过断层F4-4的第一个循环预注浆,即隧道过断层F4-4的开始段,与计算模型的剖面1相对应。根据实测结果,此次注浆循环后隧道上半断面10个检查孔总共的出水量为2.145 6 m3/d。10个检查孔的出水量仅为上隧道上半断面的涌水量值,如果近似考虑隧道上半断面和下半断面的涌水量相等,整个隧道开挖出水量大约为4.29 m3/d,而用数值分析法和公式法的计算结果分别为4.35 m3/d和4.50 m3/d。因此可以说明,此循环注浆达到了预期设计目的。

5 结论

通过隧道开挖涌水量计算和注浆后隧道出水量实测两方面对海底隧道穿越断层F4-4时预注浆的效果进行检查与评价,可以得出如下结论。

(1)公式法计算隧道开挖涌水量有很多的不足,主要是由于公式法的一些假设与实际隧道围岩的地质情况有一定的差距；数值法在求解边界条件复杂、本构关系复杂的问题上有很大的优势,涌水量计算结果较为合理,在计算过程中需特别注意渗透系数的选取、计算模型大小、网格划分质量等条件。

(2)比较两种方法的计算结果可知,基本上利用数值法的计算结果要大于公式法的计算结果,原因主要在于数值法考虑的隧道围岩地质特性和隧道断面形状与实际更符合些。

(3)当采用不同注浆圈厚度和不同注浆圈渗透系数时,隧道开挖涌水量的变化明显有一定的规律,主要表现为两方面：一方面,随着注浆圈厚度的增加隧道开挖涌水量减小,但当注浆圈厚度大于5 m后,3个剖面的隧道开挖涌水量的变化趋于平缓。如果按注浆圈厚度为5 m和Kr/Kg=5时进行比较,3个剖面的涌水量分别为4.35、9.33、4.20 m3/d,而在未注浆的情况下,三者分别为9.11、17.40、7.35 m3/d,即涌水量分别减少了54%、46%和43%。另一方面,在相同注浆圈厚度的情况下,随着注浆圈渗透系数的减小,隧道开挖涌水量也相应的减小,但对于不同的隧道围岩地质,当注浆圈渗透系数小于一定值的时候,隧道开挖涌水量的减少就会变得不明显。当Kr/Kg=5时,相对于未注浆隧道的涌水量减小了54%,并且会随着Kr/Kg值的增大涌水量会进一步减少,但变化会越来越小。

(4)通过如上计算过断层F4-4开始阶段时,用公式法、数值法及实测所得的隧道涌水量分别为：4.50、4.35、4.29 m3/d,三者大小相近,说明本循环注浆达到了设计预期目标。

[1]王建秀,朱合华,叶为民.隧道涌水量的预测及其工程应用[J].岩石力学与工程学报,2004,23(7):1150-1153．

[2]丁万涛,李术才,徐帮树，等.隧道涌水量解析公式在海底隧道工程应用研究[J].地下空间与工程学报,2008,4(4):662-664．

[3]刘继国,朱光仪,郭小红，等.厦门海底隧道建设中涌水量流固耦合数值模拟[J].现代隧道技术,2006,43(2):34-38．

[4]姬永红,项彦勇.水底隧道涌水量预测方法的应用分析[J].水文地质工程地质,2005(4)：84-87．

[5]李廷春,李术才,陈卫忠，等.厦门海底隧道的流固耦合分析[J].岩土工程学报,2004,26(3):397-401．

[6]毕焕军.裂隙岩体数值法预测计算特长隧道涌水量的应用研究[J].铁道工程学报,2000(1)：59-62．

[7]许巧详,刘 斌,金 明,等.地铁隧道穿越江河地质稳定性及渗流特性数值分析[J].中国安全生产技术,2007,3(1):62-65.

[8]Manuel M, Luis M, Jose M. Prediction and analysis of subsidence induced by shield tunneling in the Madrid metro extension. Canada. Geotech J., 2002,39:1273-1287.

[9]Hakami H. Rock characterisation facility (RCF) shaft sinking numerical computations using FLAC[J]. International Journal of Rock Mechanics and Mining Sciences, 2001,38(1):59-65.

[10]李昌宁.厦门海底隧道施工中重难点分析及技术措施[J].铁道标准设计，2007(S2):1-4.

[11]汪小平.厦门东通道海底隧道涌水量分析及预测[J].铁道勘察,2008(1)：27-29．