Multicast routing algorithm based on tabu search

HUANG Lin， LAI Jun－feng， HOU Jian， DU Xue－wu

（1.School of Mathematical Science，Dalian University of Technology，Dalian 116024，China；2.Department of Mathematics，China Jiliang University，Hangzhou 310018，China；3.College of Science，Inner Mongolia University of Technology，Huhhot 010021，China）

Multicast routing algorithm based on tabu search

HUANG Lin1，2， LAI Jun－feng＊3， HOU Jian1， DU Xue－wu1

（1.School of Mathematical Science，Dalian University of Technology，Dalian 116024，China；2.Department of Mathematics，China Jiliang University，Hangzhou 310018，China；3.College of Science，Inner Mongolia University of Technology，Huhhot 010021，China）

The delay and delay variation－bounded Steiner tree problem is an important multicast routing issue in real－time multimedia networks.Such a constrained Steiner tree problem is known to be NP－complete.A multicast routing algorithm is presented，which is based on tabu search to produce routing trees having a minimal network cost under delay and delay variation constraints.The simulation shows that the algorithm is efficient for actual networks.This approach makes IP multicast utilize resources efficiently in delivering data to a group of members simultaneously.

multicast；tabu search；delay constraint；delayvariation constraint

0 Introduction

Multicast is a mechanism to efficiently support multi－point communications［1］.In order to support real－time applications，network protocols must be able to provide QoS guarantees.Several delay－constrained heuristics have been proposed［2］.However，some of these heuristics may fail to provide a low cost tree as they assume that network links are symmetric.

There are several situations in which the need for bounded variation among the path delays takes place.During a teleconference，it is important that the speaker is to be heard by all participants at the same time，otherwise，the communication may lack the feeling of an interactive face－to－face discussion.Rouskas，etal.［3］presented a heuristic algorithm that was used to construct multicast trees，which guaranteed certain bounds on the end－to－end delays and delay variations.Sheu，etal.［4］presented a multicast routing scheme on core based tree（CBT）.But they do not attempt to optimize the multicast tree in terms of cost.

Artificial intelligence technique is used for solving this problem because of its success on similar difficult combinatorial problems.For the delay and delay variation－bounded minimum cost multicast routing problem，several heuristics have been proposed［5－10］.In this paper，an efficient algorithm is presented，which is based on tabu search［11］to produce a low－cost multicast tree with delay and delay variation constraints.This algorithm is called tabu search（TS）for delay and delay variation constraints low－cost multicast routing algorithm（TSDDVMA）.TSDDVMA belongs to source－based routing algorithm，because it is assumed that sufficient global information is available to the source.The algorithm starts with an initial shortest path tree constructed by using Sheu′s algorithm［4］.Then the algorithm constructs a backup－pathsset for each destination usingK－th shortest pathalgorithm，and generates neighborhood structure.

1 Problem definition

Mathematically，the delay and delay variation－bounded minimum cost multicast routing problem can be formulated as follows.Given a graphG＝（V，E），with node setVand edge setE，define two objective functions，c（u，v）andd（u，v），on each edge（u，v）∈E.Let

（u，v）be the cost of edge（u，v）andd（u，v）be ts delay.Assume thatc（u，v）＝c（v，u）andd（u，v）＝d（v，u）.On this graph，there are a source nodes，and a set of destination nodesM，called the multicast group.The set of vertices from the setV－M－｛s｝is called Steiner vertices.It tries to construct a delay and delay variation－bounded Steiner treeTrooted ats，that spans the destination nodes inMsuch that for each nodevinM，the delay on the path from

tovis bounded by a delay constraintΔ，and at the same time，the inter－destination delay variation is also bounded by a constraintδ.Formally，for eachv∈M，ifp（s，v）is the path nTfromstov，then

Delay and delay variation－bounded minimal cost multicast tree is a delay and delay variation constraints Steiner treeTsuch that

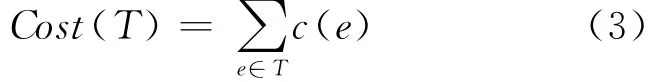
s minimized and satisfies the Inequalities（1），（2）.

2 Multicast routing algorithm with delay and delay variation constraints

The number of possible multicast trees in a computer network of a moderate size is extremely large.Furthermore，because of the multiobjective nature of the problem and the various cost parameters，it is not clear what constitutes the best tree.Modern iterative heuristics such as TS have been found effective n dealing with this category of problems which have an exponential and noisy search space with numerous local optima.These iterative algorithms are heuristic search methods，which perform a nondeterministic but intelligent walk through the search space.

按照城市主体功能区与自然环境区分化的思路，大都市区进行了两个同级别不同层面的划分，即都市化地区和生态特色发展区。规划通过形成主、次级区域，实行差异化发展引导。其中，都市化地区主要以南昌、紧邻城市与县镇为重点形成的大都市核心区，生态特色发展区则主要包括九岭山生态人文特色发展区等三大发展区，处于次级区域。奉新县地处九岭山生态发展区，未来将有环城旅游带环绕，同时大都市区在整体上选择了生态保护与资源开发共进的模式，在奉新县所属区域重点建设九岭山公园，发展定位为国家级养生度假胜地。

2.1 Initial solution

For the delay and delay variation－bounded Steiner tree problem，Rouskas，etal.［3］constructed a delay and delay variation constraints Steiner tree，but the algorithm′s complexity is high.In this paper，the initial solutionT0is constructed by using DDVCA［4，5］.If DDVCA returns false，then the algorithm may fail to obtain a feasible solution.

2.2 Backup－paths－set

For each destination nodev∈M，firstly compute least cost paths fromstovby usingK－th shortest path algorithm to construct a backup－paths－set［7，12－14］.LetBvbe the backup－paths－set for destination nodev，then

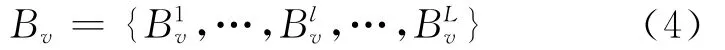
If there are nokdifferent paths from the source to destination nodevsatisfing the delay constraint，it is shown that the delay constraint is too small，then negotiate with destinations node above the delay constraint［3］.

2.3 Neighborhood structure

A neighbor structure of the solutionTnowis defined as：

whereis thes－th backup path for destination nodev.

See the following definitions about the multicast tree.Given a networkG＝（V，E）and a multicast treeT，p（s，v）is a path fromstov，fors，v∈V.

Definition 1Adding path（∪）.Add a pathp（s，v）intoT，denoted byT∪p（s，v），T∪p（s，v）＝｛e｜e∈Tore∈p（s，v）｝（6）

Theorem 1Given a networkG＝（V，E），a source nodes，destination node setM.Δandδare the delay bound and the delay variation bound of multicast session，respectively.SupposeTis a subtree，andΔT＜Δ，δT≤δ.Sub（M）is the destinations covered inTso far，andSub（M）≤M.Usedmaxanddminto represent the maximal delay and minimal delay of the path among the paths fromsto each destination ofSub（M）inT，respectively.m∈M，m贡Sub（M），ifp（s，m）satisfies max｛0，dmax－δ｝≤d（p（s，m））≤min｛dmin＋δ，Δ｝andT′＝T∪p（s，m），then

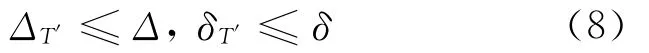
Theorem 1shows that the procedure of constructing a feasible tree meets delay and delay variation bounds，if the delay of a path fromsto next uncovered destination satisfies max｛0，dmaxδ｝≤d（p（s，m））≤min｛dmin＋δ，Δ｝，and then the tree after adding this path is still a feasible tree［5］.

2.4 Tabu moves

A tabu list is maintained to prevent returning to previously visited solutions.This list contains information that forbids the search to some extent from returning to a previously visited solution.In approach of this paper，a multicast tree is considered as an element of tabu list.

2.5 Aspiration criterion

Aspiration criterion is a device used to override the tabu status of moves whenever it is appropriate.It temporarily overrides the tabu status if the move is sufficiently good.The aspiration criterion must make sure that the reversal of a recently－made move（that is，a move in the tabu list）leads the search to an unvisited solution，generally a better one.In this approach，if the cost of a tabu candidate solution is better than current solution，then it replaces current solution and is considered as new current solution.

2.6 Termination rule

A fixed number of iterations have been used as a stopping criterion，and experimented with different values of iterations.It is found that for all the test cases，the TSDDVMA converges within a maximum of 200iterations.The pseudo code for TSDDVMA is as follows：

Procedure TSDDVMA（G＝（V，E），s，M，Δ，δ，c，d）

2.7 Time complexity

Theorem 2The time complexity of TSDDVMA isO（kmn3），wheremis group size andnis network size，kis the parameter ink－SPA.

ProofThe time complexity of generating initial solution by using DDVCA isO（mn2）［4］，and the complexity of constructing backup－paths－set by usingk－SPA isO（kmn3）［3，7－10，13，14］.Because one iteration costsO（k），thus，forQiterations，the cost becomesO（Qk）.So the worst time complexity of the algorithm isO（mn2＋kmn3＋Qk）.The termQkis usually much smaller thankmn3，so the time complexity of TSDDVMA isO（kmn3）.

3 Simulation results and discussion

The TSDDVMA algorithm described in this paper has been tested on several randomly generated networks based on the Waxman′s algorithm［15］.

In the first set of experiments，TSDDVMA is compared with DDVCA［4］and SADDVMA［5，6］for cost performance，where DDVCA is a delay and delay variation－bounded Steiner tree without considering the tree cost.Fig.1shows the tree costctfor varying network sizenwith the group sizem＝4and 6respectively with an average node degree of 3，Δ＝0.40andδ＝0.20.The source nodes and destination nodes vary in each time experiments.It can be seen from Fig.1that TSDDVMA has a better cost performance than DDVCA，and is close to SADDVMA，and could construct low－cost trees which satisfy the given delay and delay variation bound and manage the network resources efficiently.

In the second set of experiments，Fig.2shows the tree cost for varying network sizenwith the group sizem＝5，an average node degree of 3.5（around）and 4.0respectively，Δ＝0.40andδ＝0.20.In general，TSDDVMA has good cost performance and is feasible and effective.

Finally，consider the iteration times of the algorithm.Fig.3shows the tree cost for varying iteration times with the number of network nodesn＝40and 50respectively，group sizem＝4，5and 6.The algorithm converges quickly，and has desirable characteristics of approximation iterative heuristics，which satisfies the real－time requirements of multimedia network.

Fig.1 Tree cost ctversus network size nforΔ＝0.40，δ＝0.20and average node degree 3

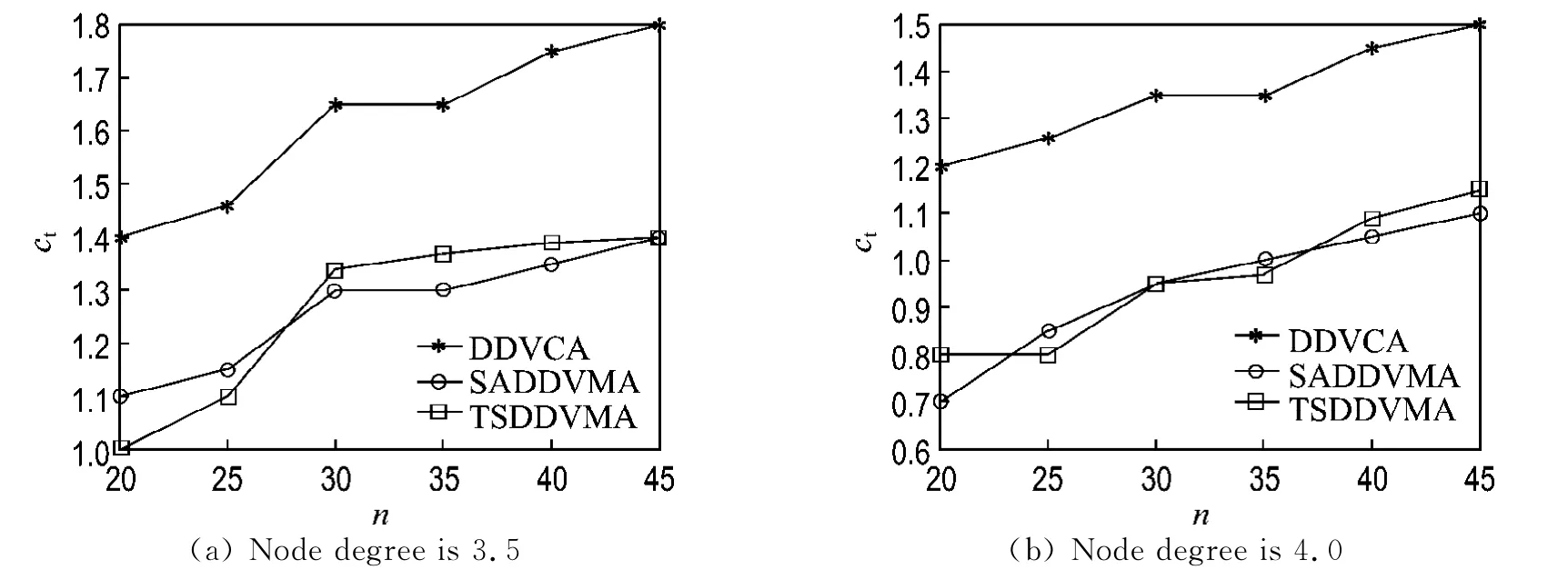
Fig.2 Tree cost ctversus network size nforΔ＝0.40，δ＝0.20and m＝5

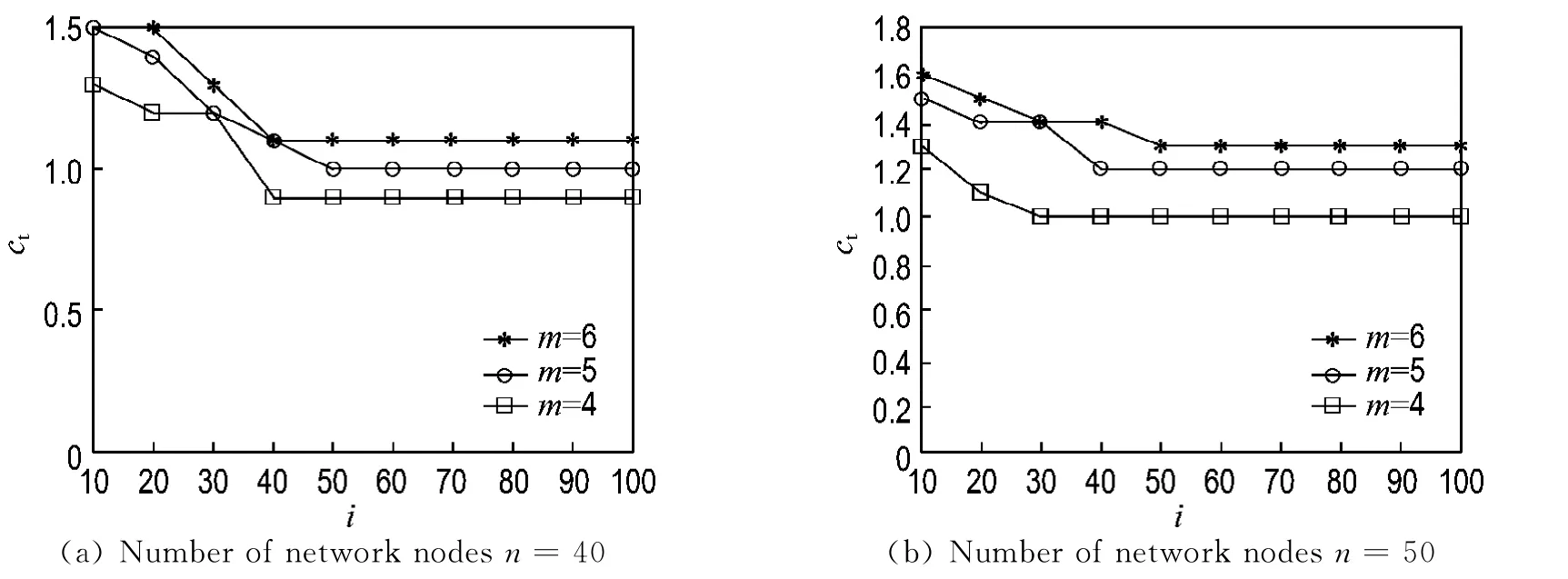
Fig.3 Tree cost ctversus iteration times i for example network

4 Conclusions

Simulations demonstrate that the algorithm of this paper performs excellent performance of cost，rapid convergence and better real－time property.

［1］BERTSEKAS D，GALLAGER R.Data Network［M］.NJ：Prentice－Hall，1992

［2］KOMPELLA V P，PASQUALE J C，POLYZOS G C. Multicasting routing for multimedia communication［J］.IEEE Transaction on Networking，1993，1（3）：286－292

［3］ROUSKAS G N，BALDINE I.Multicast routing with end－to－end delay and delay variation constraints［J］.IEEE JSAC，1997，15（3）：346－356

［4］SHEU P R，CHEN S T.A fast and efficient heuristic algorithm for the delay－and delay variation－bounded multicast tree problem［J］.Computer Communication，2002，25：825－833

［5］ZHANG K，WANG H，LIU F Y.Distributed multicast routing for delay and delay variation－bounded Steiner tree using simulated annealing［J］.Computer Communication，2005，28：1356－1370

［6］ZHANG K，WANG H，LIU F Y.An efficient algorithm based on simulated annealing for multicast routing with delay and delay variation constraints［C］／／Proceedings of the 19th International Conference on Advanced Information Networking and Applications（AINA′5）.Washington D C：IEEE Computer Society Press，2005

［7］SUN W S，LIU Z M.Multicast routing based neural networks［J］.Journal of China Institute of Communications，1998，19（11）：1－6（in Chinese）

［8］LU Guo－ying，LIU Ze－min.Multicast routing based on ant－algorithm with delay and delay variation constraints［C］／／The 2000IEEE Asia－Pacific Conference on Circuits and Systems.Tianjin：IEEE，2000

［9］ZHANG S B，LIU Z M.A new multicast routing algorithm based on chaotic neural networks［J］.Chinese Journal of Computer，2001，24（12）：1256－1261（in Chinese）

［10］GUO W，XI Y G.Minimal cost multicast routing problem with end to end delay and delay variation constraints［J］.Journal of China Institute of Communications，2001，22（6）：13－20（in Chinese）

［11］WANG L.Intelligent Optimization Algorithms with Applications［M］.Beijing／Heidelberg：Tsinghua University Press／Springer，2001

［12］SALAMA H F，REEVES D S，VINIOTIS Y.Evaluation of multicast routing algorithms for real－time communication on high－speed networks［J］.IEEE Journal on Selected Areas in Communication，1997，15（3）：332－345

［13］SHI J，ZOU L，DONG T L.The application of genetic algorithm in multicast routing［J］.Acta Electronica Sinica，2000，28（5）：88－89（in Chinese）

［14］WANG H，FANG J，WANG H，etal.TSDLMRA：an efficient multicast routing algorithm based on Tabu search［J］.Journal of Network and Computer Applications，2004，27（2）：77－90

［15］WAXMAN B M.Routing of multipoint connections［J］.IEEE Journal on Selected Areas in Communication，1988，6（9）：1617－1622

1000－8608（2010）05－0801－05

基于禁忌搜索的组播路由算法

黄 林1，2， 赖俊峰＊3， 侯 剑1， 杜学武1

（1.大连理工大学数学科学学院，辽宁大连 116024；2.中国计量学院数学系，浙江杭州 310018；3.内蒙古工业大学理学院，内蒙古呼和浩特 010021）

实时多媒体网络中，带延迟与延迟抖动约束的斯坦利树问题是一个研究热点.这种带约束的斯坦利树被证明是NP－完全问题.提出了一种基于禁忌搜索的带延迟与延迟抖动约束最小代价组播路由算法.实验结果表明，该算法对于实际网络是有效的.这种方法使得IP组播把数据同时发送到组成员时有效地利用了网络资源.

组播；禁忌搜索；延迟约束；延迟抖动约束

TP393

A

2008－05－04；

2010－06－05.

内蒙古工业大学科研基金资助项目（X200829）.

黄 林（1979－），男，博士，E－mail：goodluckyoume＠yahoo.com.cn；赖俊峰＊（1978－），男，讲师，E－mail：ljfimpu＠sina.com.

by：2008－05－04； Revised by：2010－06－05.

Supported by：Fund of Inner Mongolia University of Technology（X200829）

s：HUANG Lin（1979－），Male，Doc.，E－mail：goodluckyoume＠yahoo.com.cn；LAI Jun－fen＊（1978－），Male，Lecturer，E－mail：ljfimpu＠sina.com.