第40届国际物理奥林匹克竞赛实验试题简介

荀 坤,王若鹏,陈晓林

(北京大学 物理学院,北京 100871)

1 引 言

第40届国际物理奥林匹克竞赛于2009年7月12日至7月19日在墨西哥的梅里达市(Merida)举行.代表中国参赛的5名中学生全部都获得了金牌,其中,史寒朵同学还成为了国际物理奥林匹克竞赛史上第一个获得总分第一的女生,此外,她还获得了本届比赛的实验第一名奖和女生第一名奖.

本届竞赛的实验部分由2道光学题组成,分别是利用刀片锐边的衍射测量激光波长和测量云母片的双折射量.2个实验使用了相同的激光光源和光学平台,学生可以自己选择做题的顺序.赛会统一提供计算器、透明胶带、粘贴纸、剪刀、三角尺、笔、纸和绘图纸等.试题有20多页,本文不得不对其中的知识介绍部分作较多删节,但会尽量完整地保留考试内容.由于篇幅限制,试题解答尽量采用赛会提供的标准答案.最后,简单分析中国考生的答题情况.

2 试题概要

2.1 实验装置

除木制光学平台外,2个实验试题还要共用1台二极管激光器(包括激光器支架和电源)及1面可调节反射镜,它们的安装方式见图1.实验中用到的其他实验器材见图2.

实验A需用到的器材有:

1)固定在方柱上的短焦会聚透镜(C);

2)安放在硬纸框内的刀片(D1),滑动导轨(D2),带滑槽的有机玻璃支架(D1,已装在D2上);

3)带有游标尺(1/20 mm)的观察屏(E);4)放大镜(F);

5)30 cm的直尺(G);

6)游标卡尺(H);

7)钢卷尺(I).

实验B用到的器材有:

1)2片装在幻灯片框内的偏振片,每个偏振片还配有1个有机玻璃座(J);

2)装在塑料圆筒内的云母薄片(K);

3)光探测装置,包括装在塑料盒中的光探测器、连接用导线、用于固定光探测器的泡沫套及1台用于测量光探测器输出电压的万用表(L).

2.2 实验内容

2.2.1 实验A内容

按图1的指示,让激光束(A)经反射镜(B)反射后,再通过焦距为几cm的透镜(C).可将该透镜的后焦点看成点光源,从该点光源发出直接到达的球面波与经刀片锐边散射后再到达的柱面波会相互干涉,在屏上形成如图3所示的衍射图像.

图3 观察屏上看到的典型衍射图

按透镜后焦点与刀片的位置关系,可以有2种光路配置,分别见图4和图5.

图4 配置Ⅰ,刀片在透镜的焦点之前

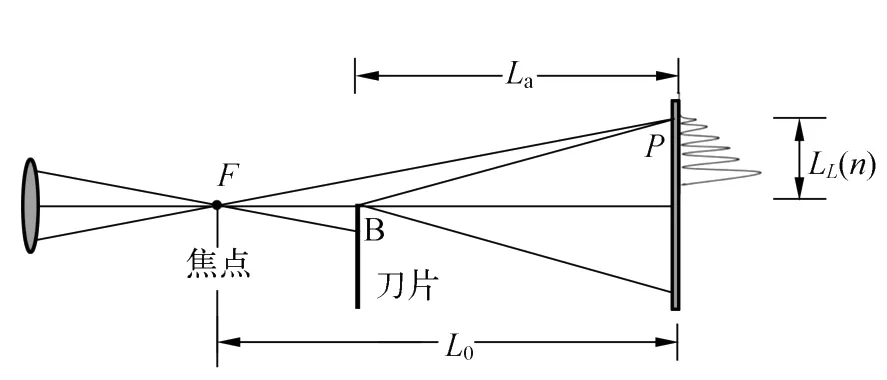
图5 配置Ⅱ,刀片在透镜的焦点之后

1)任务A 1 光路设计(1.0分)

设计一套光路,以获得图3所示的干涉图像.要保证从焦点到屏的距离L0远大于焦距.

a.在所给的光学平台图上绘出实验装置的草图,即在光学平台图上标出不同设备的“标记符”,还可以在此基础上加画一些简单内容以使设计更清楚.

b.可以用1张白卡片来跟踪光束的路线,以帮助调节激光束的方向.

c.在实验装置草图上示意绘出激光束的传播路线,给出测得的激光束相对光学平台的高度 h.

请熟悉上述实验装置.在屏上应该能看到10来条竖直的线状条纹,请读出暗纹的位置(可以用放大镜更清楚地看到条纹的位置).观察条纹最好的位置是在被照射的屏(E)的背面.所以,屏上的标尺应该面向光学平台外侧.如果光路正确,只需简单滑动导轨(D2)使刀片(D1)前后移动,即可分别观察到配置Ⅰ和配置Ⅱ对应的2种衍射条纹花样.

由前述图4和图5知,有5个基本长度.

L0为从焦点到屏的距离;Lb为从刀片到屏的距离(配置Ⅰ);La为从刀片到屏的距离(配置Ⅱ);LR(n)为 n级暗纹的位置,配置Ⅰ;LL(n)为 n级暗纹的位置,配置 Ⅱ.

无论是配置 I还是配置Ⅱ,第一个暗纹都是最宽的,对应 n=0.

实验装置必须满足:对配置Ⅰ,LR(n)≪L0,Lb;对配置Ⅱ,LL(n)≪L0,La.光波的干涉现象是由于同一点发出的光波的光程差造成的.根据相位差的不同,波可以相消(相消干涉)形成暗纹;波也可以相长(相长干涉)形成亮纹.

详细分析这些波的干涉,可给出如下产生暗纹的条件.对配置Ⅰ:

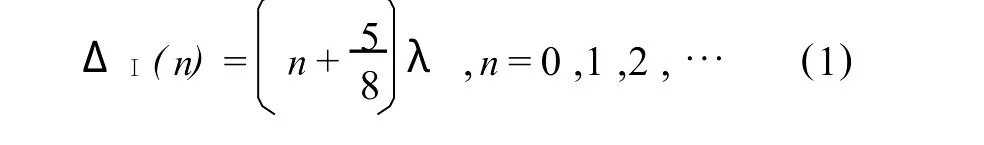
对配置 Ⅱ:

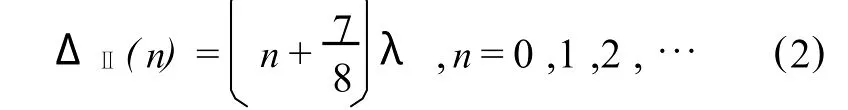
这里λ是激光束的波长,对配置Ⅰ和配置Ⅱ,光程差ΔⅠ和ΔⅡ分别为

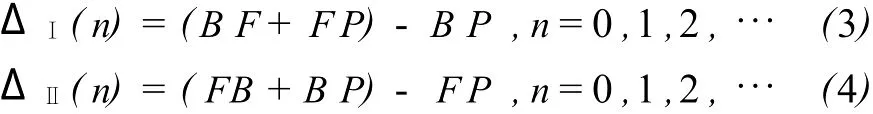
2)任务A 2 光程差的表达式(0.5分)

假设式(3)和式(4)分别满足:LR(n)≪L0,Lb和LL(n)≪L0,La(需要确认装置是否确实满足这些条件),求出ΔⅠ(n)和ΔⅡ(n)的近似表达式,用 L0,L b,L a,LR(n)和 LL(n)表示.当 x≪1

时,可以用(1+x)r≈1+rx这一近似公式.

使用上述公式的实验困难是 L0,LR(n)和LL(n)不能精确测量.L0测不准的原因是不容易找到透镜焦点的位置;后2个量测不准的原因是它们的零点位置难以确定.

为解决LR(n)和 LL(n)的测量困难,可以选择观察屏(标记符为 E)标尺的零点(0)作为测量所有条纹位置的参考零点.令 l0R和 l0L分别为定义LR(n)和LL(n)时所用的零点位置,此时,它们实际上是未知的.再令lR(n)和lL(n)为条纹到所选取的原点的距离.因此,应有:

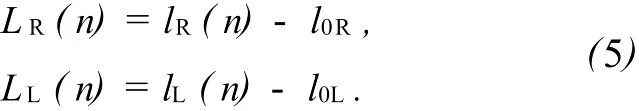
3)任务A 3 测量暗条纹的位置和刀片的位置(3.25分)

a.对配置Ⅰ和配置Ⅱ,分别测量不同条纹编号 n下暗条纹的位置lR(n)和lL(n).将测量结果记入表1中.对每种配置,测量的条纹位置数要尽可能达到或超过8.

b.报告测得的刀片位置Lb和La,并注明所用测量仪器.

c.为分析简单和结果精确起见,不要由Lb和La计算得到 d=Lb-La,而是要直接测量,并要标明所用的测量仪器.

4)任务A 4 数据分析处理(3.25分)

完成前面测量后应该就已经可以得出 l0R和l0L,当然也包括波长λ的值.

a.设计一个方案来得到这些值,并写出所需的表达式或方程.

b.结果要包括误差分析.可以用表1,也可以用自己的表来给出结果,但要确保表中各栏名称能清楚反映其内容.

c.用所给图纸选适当变量画图得到所需量.

d.分别写出带不确定度的l0R和 l0L的值.

5)任务A 5 计算λ(2分)

综上所述，打孔注药防治黄斑星天牛不但防治效果好，不污染环境，不杀伤天敌，且用药量少，成本低，在通常情况下建议使用氧化乐果，既节约又有效，可大面积推广使用，对受害严重的也可以进行3次注药防治。

写出λ值的计算结果,包括不确定度和得到它的过程.在计算λ时,凡出现 Lb-La之处,均可以用 d代替,并使用 d的测量值来作计算.

2.2.2 实验B内容

如云母一类的双折射晶体,其折射率与电场的方向也即光的偏振方向有关.对于传播方向与云母片表面垂直的光,云母薄片有2个相互垂直的特殊轴向,称之为轴1和轴2,见图6.

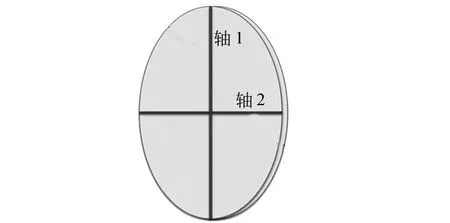
图6 云母薄片的2个特殊轴向

当入射光偏振方向与轴1或轴2平行时,云母分别相当于折射率为 n1或 n2的介质,经过云母片前后,光的偏振方向均不会发生改变.当入射光偏振方向与轴1夹角为θ时,可以将入射光视为沿轴1和轴2两个方向偏振的光的叠加.经过云母后的透射光可看作是2个分别沿轴1和轴2方向偏振但两者相位不同的偏振光的叠加.一般说来,透射光的偏振状态和入射光的偏振状态不再一样,还存在垂直于入射光偏振方向的偏振成分,见图7.

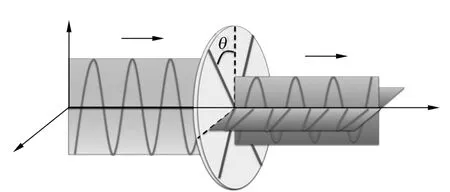
图7 轴1与入射光偏振方向有夹角θ

将偏振方向与入射光偏振方向平行和垂直的光强分别记作 IP和 IO.这2个光强的大小与夹角θ、波长λ、云母片厚度L及折射率差|n1-n2|有关.折射率差|n1-n2|被称为介质的双折射量,是本实验要测量的内容.

需指出的是,光探测器测量的是照射到探测器上的光强,与光的偏振态无关.由于还与其他因素(如云母对光波的吸收)有关,IP(θ)和IO(θ)与夹角θ的关系复杂,可定义归一化光强:

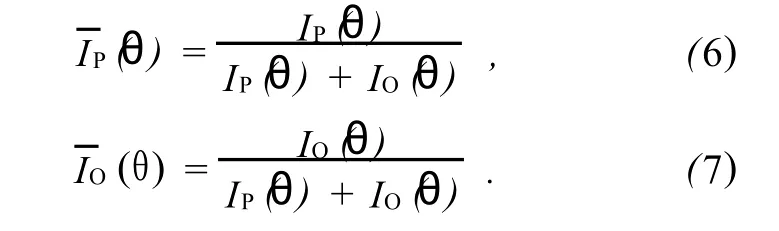
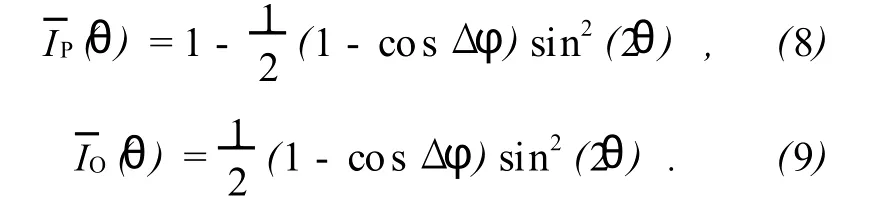
这里相位差Δφ由下式给出,

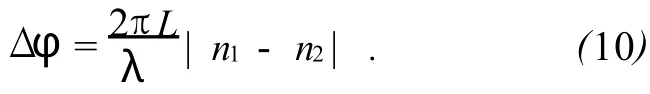
1)任务B1 设计一个测量 IP和 IO与夹角θ关系的装置.θ可以是与轴1和轴2中任意一个的夹角.用(+)标记起偏器的透振方向,分别用(+)和(-)来标记检偏器透振方向与起偏器平行和垂直.测量 IP和 IO的装置分别占0.5分.

调整激光束,使其与光学平台平行,并通过装有云母片的圆筒的中心.可以用白色厚纸片来确定激光束的径迹,还可以通过调节反射镜来改变光束的走向.

当有光照射到光探测器上时,会有电压输出,此电压与光强成正比,可以用万用表测量.虽然在没有激光入射到光探测器上的情况下,会有输出电压小于1 m V的背景光强,但在进行光强测量时不要作背景光强修正.

2)任务B2 角度刻度的标定

装载云母片的圆筒外壁标有等角度的分刻线.写出2条相邻刻线之间的角度间隔(用度表示).(0.25分)

找到夹角θ等于0时的刻度位置对数据分析是十分重要的.最好先确定云母的一个光轴(轴1)与入射光偏振方向平行时的刻度位置(这一般不与任何刻线重合).选择最接近此位置的刻线作为夹角测量的临时原点,将相对于临时原点测得的角度记为¯θ,稍后,再用¯θ零点值来修正.

3)任务B3 测量 IP和 IO对于你认为必要的若干¯θ取值,测量光强IP和IO.将测量结果填入表2中.应在同一云母片位置(即相同的取值)分别测量光强 IP和 IO.(3.0分)

θ角的零点由轴1的位置定义.可采用作图的方法或数值计算的方法来确定.在极大值或极小值附近,光强曲线可用抛物线来近似:

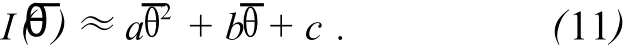
抛物线的极大值或极小值点由下式给出:

5)任务B5 选择适当的变量

6)任务B6 数据分析与相位差

将数据分析所用变量的值填入表3中,要采用修正后的角度θ值并包含不确定量.在坐标纸上画出数据点.(1.0分)

a.以获得相位差Δφ为目的,对上面的数据作统计分析,给出结果及结果的不确定度,并写出分析中所用到的方程或公式.将此处统计分析得到的结果,以直线的形式画在(已标有数据点的)坐标纸上.(1.75分)

b.计算相位差Δφ及其不确定度的值,结果用弧度表示.在区间[0,π]确定相位差的值.(0.5分)

7)任务B7 计算双折射量|n1-n2|

注意到在相位差Δφ上增加2π的整数倍或改变Δφ的符号,都不会改变光强的大小,但双折射量|n1-n2|却会改变.所以在采用任务B6中得到的Δφ来计算双折射量|n1-n2|时须作如下处理:

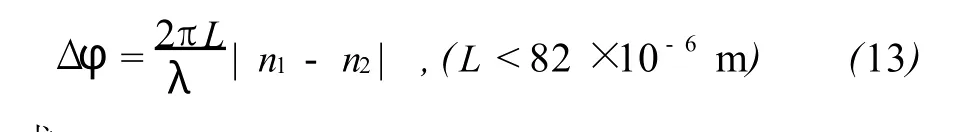
或

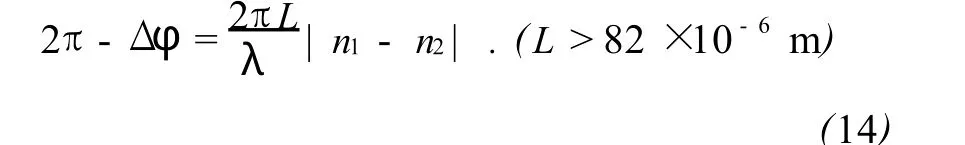
这里L是云母片的厚度,其值可在装云母片的小圆筒上找到,单位为μm.L的不确定度可以取为1×10-6m.这里的波长可采用试题A中测得的值,也可用红光区间620×10-9～750×10-9m的平均值.写出L,λ和|n1-n2|的值及不确定度,并写出用于不确定度计算的公式.(1.0分)

3 试题解答

3.1 试题A解答

1)按图8配置光路.调节反射镜倾角和透镜高度,保证激光光束始终与光学平台平行.短焦透镜C与观察屏间距离尽可能远,并能通过滑动导轨分别得到配置I和配置Ⅱ对应的2种衍射条纹花样.测量激光束距光学平台的高度,其值为h±Δh=(5.0±0.05)×10-2m.

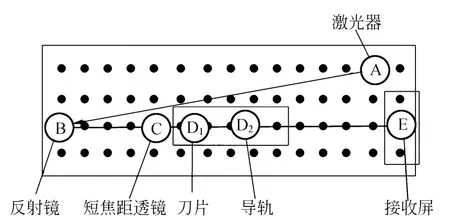
图8 实验A的光路示意图

2)对配置Ⅰ,有:

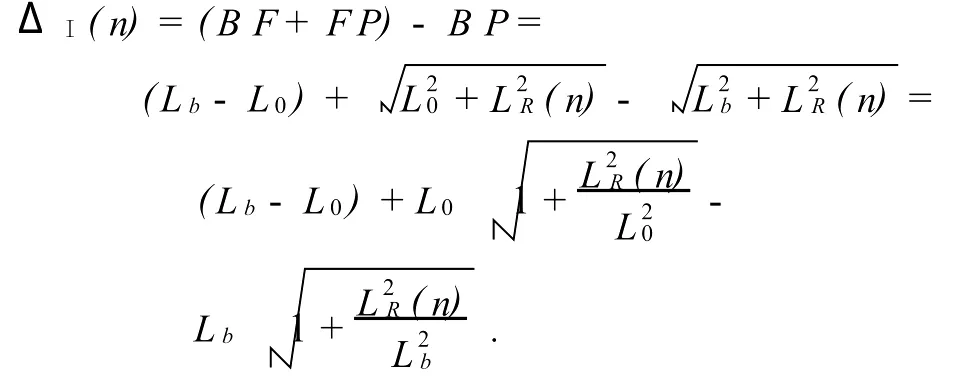
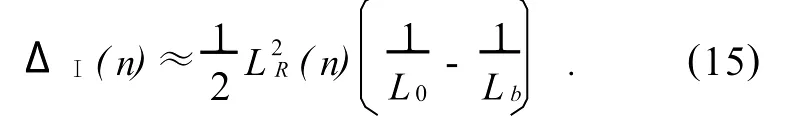
类似地,对配置Ⅱ,有:

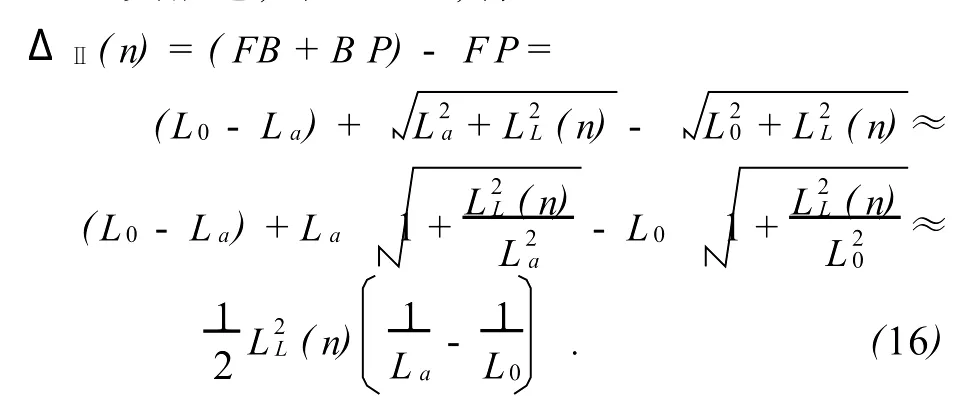
3)适当调节刀片位置,以使能在配置Ⅰ和配置Ⅱ情况下在屏上分别观察到相应的衍射图.测量暗纹的位置并记录于表1中.表中 xR=

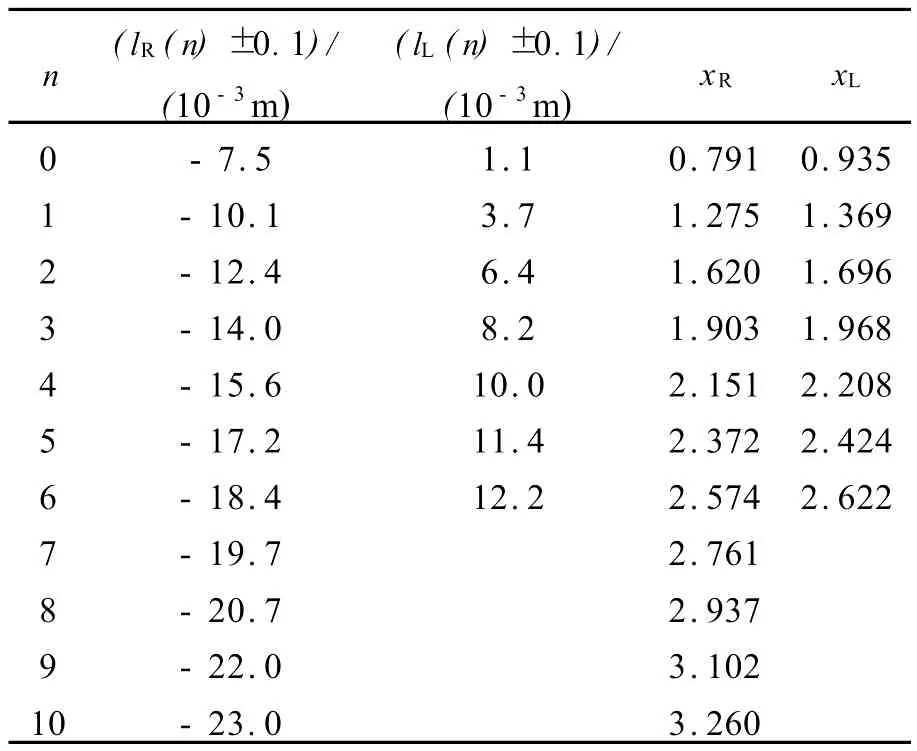
表1 衍射图样暗条纹的位置

测量得到刀片位置:

Lb±ΔLb=(653±1)×10-3m(用卷尺测);

La±ΔLa=(628±1)×10-3m(用卷尺测);

d=Lb-La=(24.6±0.1)×10-3m(用游标卡尺测).

4)用表1数据分别画出 lR-xR和 lL-xL关系图,并作线性拟合,如图9所示.

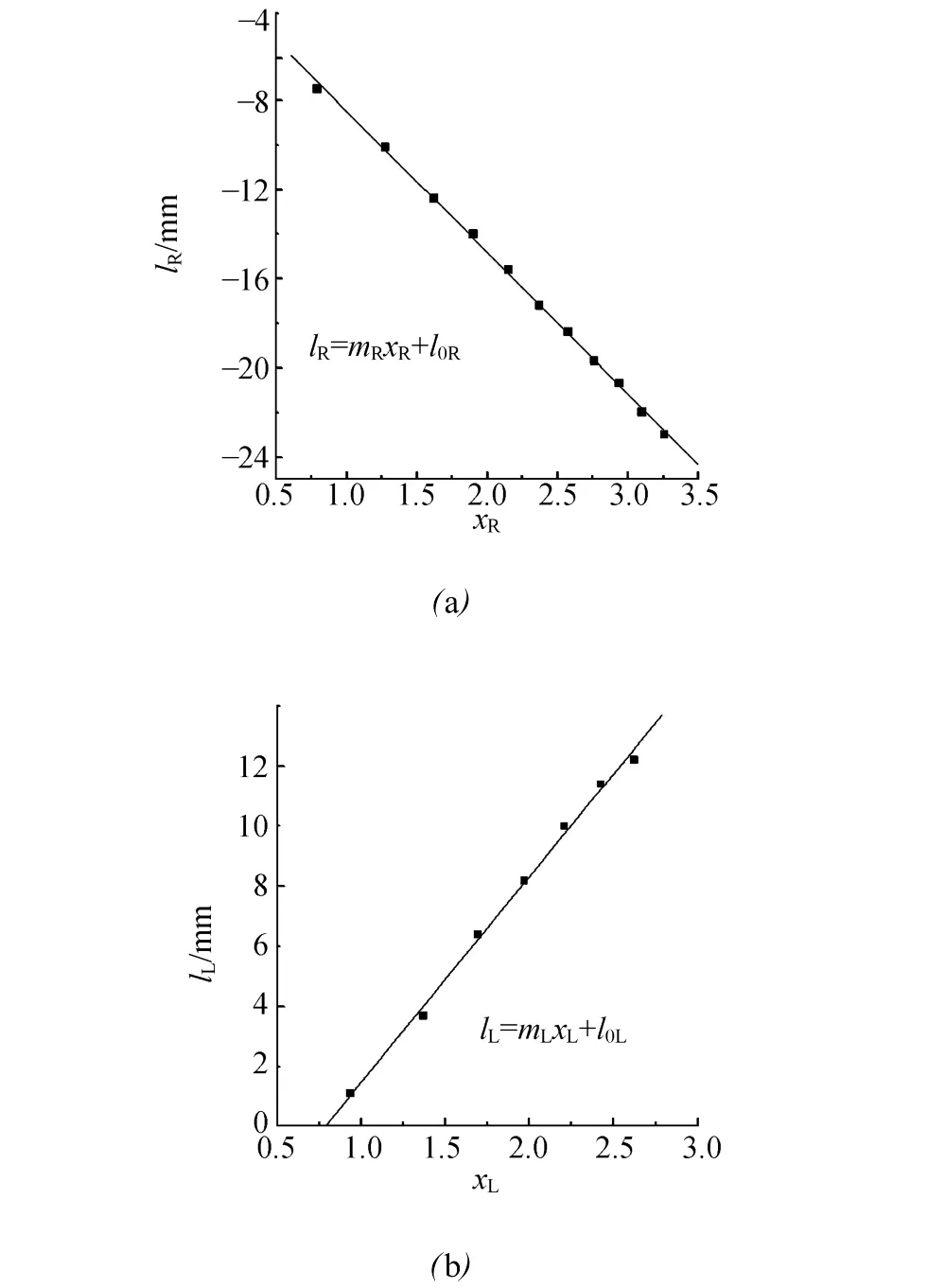
图9 l R-x R和l L-x L关系图及线性拟合

赛会提供的计算器并不具有线性拟合功能,试题还要求选手写出线性拟合以及各拟合量的误差分析公式,因篇幅所限,这里不再列出,读者可以从任何一本大学实验教材上查到.线性拟合得到的结果为:mR=(-6.35±0.07)mm,l0R=(-2.1±0.2)mm;mL=(6.8±0.2)mm,l0L=(-5.3±0.4)mm.

5)对比式(1)和式(15)及式(2)和式(16)有:

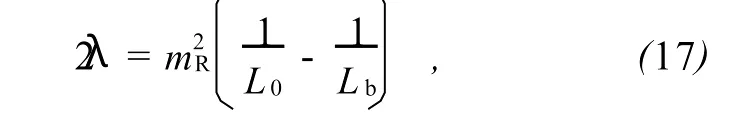
和

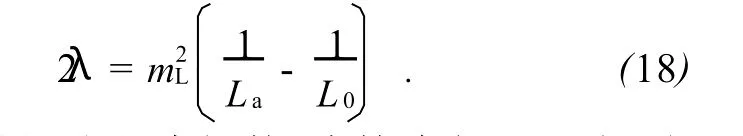
注意到L0实际上是未知的,将其消去,可以得到:

将各测量值代入式(19)得:

λ的不确定度为

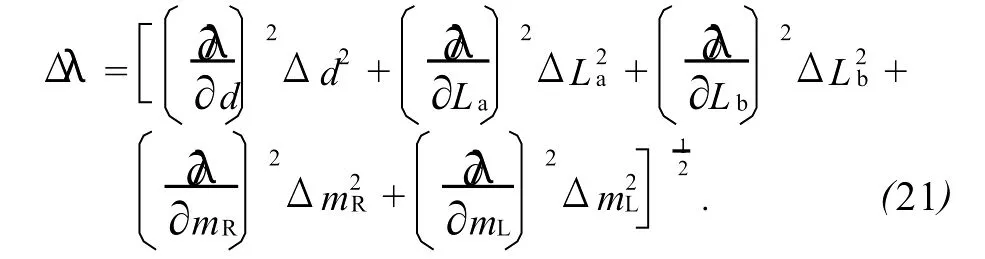
注意到,根号内前3项远小于后2项,m2R≈m2L,且ΔmL≈3ΔmR,近似有 :

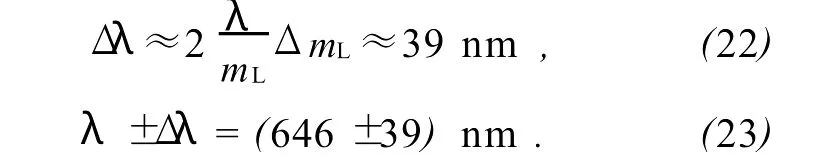
3.2 试题B解答

1)图10(a)和(b)分别为测量 IP和 IO的光路示意图,(a)与(b)的唯一差别是检偏器的透振方向分别与起偏器的透振方向平行和垂直.

2)安放云母片的圆筒外壁上共有100条分刻线,故2条相邻刻线间的角度间隔为θint=3.6°.安放云母片的圆筒被嵌入密合的外套座内,转动圆筒就可以改变云母片光轴的取向.外套座上有一刻线,用于指示圆筒的相对角位置.

按图10(b)安置光路,转动安有云母片的圆筒(K)使探测器(L)检测到的光强最弱.此时,云母片的一个光轴即与起偏器的透振方向一致.将此时最靠近外套座上刻线的圆筒上的刻度线作为临时角度零点,将圆筒相对此零点转过的角度记为¯θ.

图10 测量 I P和 I O的光路示意图

3)由式(8)和(9)知,只需在90°范围测量 IP和IO.因此,¯θ的取值范围-3.6°～93.6°,可以每3.6°取一点.在同一¯θ位置,改变检偏器的取向分别测量光强 IP和 IO,得到的结果记入表2中.

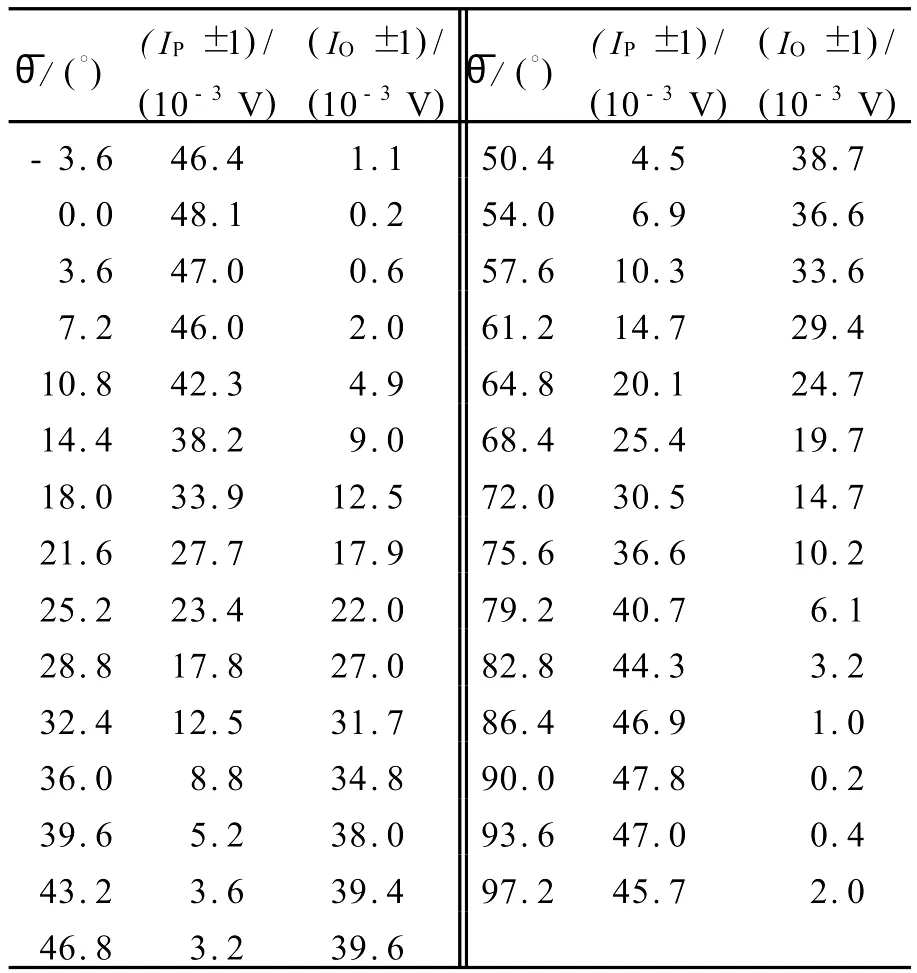
表2 I P和 I O测量结果

4)¯θ零点的位置可以由表2中前3个数据点作数值求解的方法得到(用作图的方法也可以).光强曲线可用抛物线I)≈a++c来近似.将前3个数据点的值(x1,y1)=(-3.6,1.1),(x2,y2)=(0,0.2),(x3,y3)=(3.6,0.6)代入,可解得:a=0.05,b=-0.069.于是得到

6)注意到θ从0到45°时,x=sin2(2θ)即可从0到1,可以只选表2中的12组数据来作分析,结果见表3.

表3 y= ¯I O 与 x=sin2(2θ)的关系

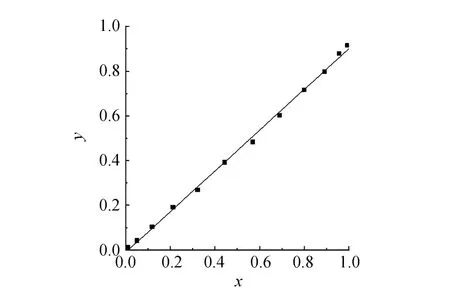
图11 y= ¯I O 与 x=sin2(2θ)的关系

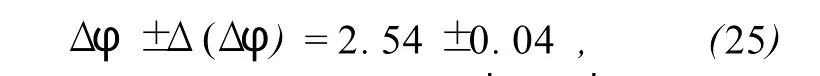
7)从安放云母片的圆筒的标签上读得云母片的厚度为:L±ΔL=(100±1)×10-6m,由实验A测得的激光波长λ±Δλ=(646±39)×10-9m.据此,求得云母片的双折射量为:

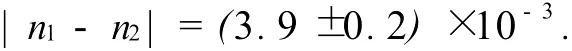
估计|n1_-n2|的误差时用到了公式:

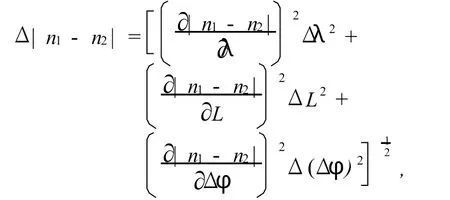
和

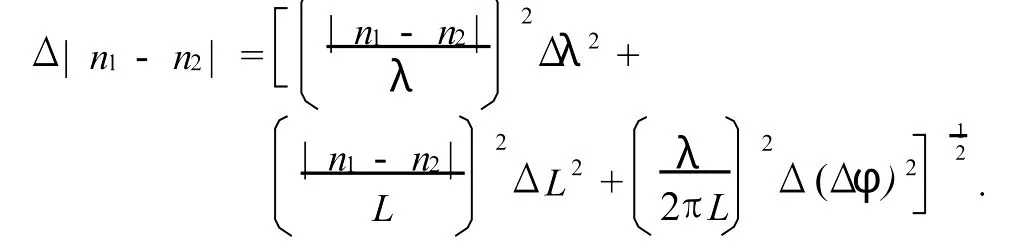
显然,λ对|n1-n2|误差的贡献远大于其他量,因此,在估计误差时可以仅仅考虑此项.

4 分 析

总起来说,本次实验考试内容比较平常,没有超出学生的知识范围,也不需要独特的构思,但对学生实验素质的要求也还是较高和全面,考察了光路设计、光路调节、公式推导、测量读数和数据处理几方面的能力.和历次实验竞赛一样,所有同学都反映时间非常紧张.只有具有清晰的物理图像、良好的实验操作素养和扎实的实验数据处理基本功的同学才可能取得令人满意的成绩.由于针对近年来国际物理奥林匹克竞赛的特点,加强了基础,特别是误差分析方面的训练,中国队取得了很好的成绩.实验A有2人得了满分,史寒朵同学更是以19.9分(满分为20分)的高分名列实验第一.

但是,同学们的答卷也暴露了一些问题.在实验A中,有一位平时实验非常好的同学,在处理数据时被卡住了,丢了5.5分,还有一位同学没有考虑到L0实际上是测不到的(因为不知道透镜的焦距),也丢了一些分.在实验B中,由于时间紧,有一位同学没有做完,其他同学也只是勉强完成.当然,按这类竞赛的性质,本来就不应该有人能完满完成全部考试内容.

[1] 吕斯骅,段家忯.新编基础物理实验[M].北京:高等教育出版社,2006.

[2] 马秀芳,沈元华.第八届亚洲物理奥林匹克竞赛中实验考题的分析[J].物理实验,2007,27(12):29-33.