采用重置参数的轨道改进算法*

刘 卫，缪元兴

(中国科学院国家天文台云南天文台，昆明 650011)

双行根数是北美防空联合司令部(NORAD)提供的太空飞行物编目及轨道根数信息。一般配合SGP4/SDP4模型进行定轨预报[1]，实际工作中由于精度等原因很多工作不能基于SGP4/SDP4模型进行，例如利用SLR资料进行科研时需要精密初始根数。如果采用TLE作初值，会出现残差过大不收敛，或者收敛到与实际状态有偏差的轨道上。对这种初始根数误差较大的精密定轨过程，本文结合两颗卫星的算例给出了一种能够利用TLE根数和激光测距资料得到精密根数的方法。首先以TLE根数为初值用精密定轨程序解条件方程[2]，然后以第一轮迭代计算结果(只采用改进后的轨道状态量)作为初始值并重置模型参数，再进行第二轮迭代计算，由于第一轮计算使得轨道状态量有了较大的改进故此时定轨计算结果能收敛到正确轨道上，定轨最终得出的RMS达到厘米级精度。此方法较好地解决了因初值不准引起的定轨计算不收敛，或收敛到与实际状态偏差大的轨道上的问题。此方法解决了使用SLR资料进行科研时无精密初始根数的问题; 另外，此方法也可为激光漫反射空间碎片精密定轨过程提供了计算思路，对空间碎片研究具有重要意义。

1 双行根数提取

双行格式如下：

第1行第3组为根数对应的历元时间，其他变量依次为轨道倾角i；升交点赤经Ω；轨道偏心率e；近地点辐角ω；平近点角M；每天运动的圈数C(圈/天)。

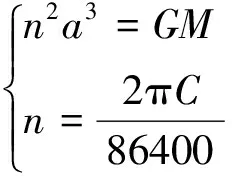
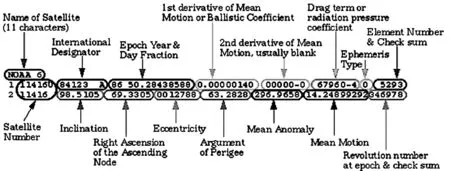
图1 双行根数格式Fig.1 The format of TLE(Two Line Elements)

2 TLE根数映射到精密定轨初始根数历元

为了与已知的SLR初始根数作比对，先将双行根数外推到给定的SLR精密根数历元时刻。

表1 已知的历元SLR精密初始根数Table 1 Precise initial orbit elements of SLR

表2 由双行根数提供的初值Table 2 TLE orbit elements

表3 外推至SLR精密初始根数对应的历元时刻Table 3 Epoch orbit elements extrapolated from the precise initial elements of SLR

由以上相同历元的坐标、速度相对比，可见双行根数位置误差为千米量级。由于TLE给出的是平根数，此转换忽略了短周期项部分，所以带入较大误差。

表4 外推所采用的摄动模型Table 4 Models used in the prediction

其他比如章动、岁差以及天文常数均按照IERS Conventions(2003)[4]进行处理。

3 用SLR和TLE作初值的具体算例

采用AJISAI激光卫星作为具体算例。

(1)首先采用全球激光网精密根数作初值，利用3天的激光测距资料进行定轨计算。

表5 计算环境Table 5 The caculation environment

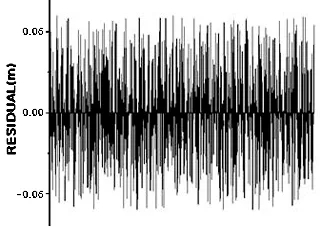
图2 以SLR精密根数作初值迭代收敛后的资料的残差分布图

表6 精密根数最后一次迭代的RMSTable 6 The RMS errors at the last iteration calculated with the precise elements

续 表

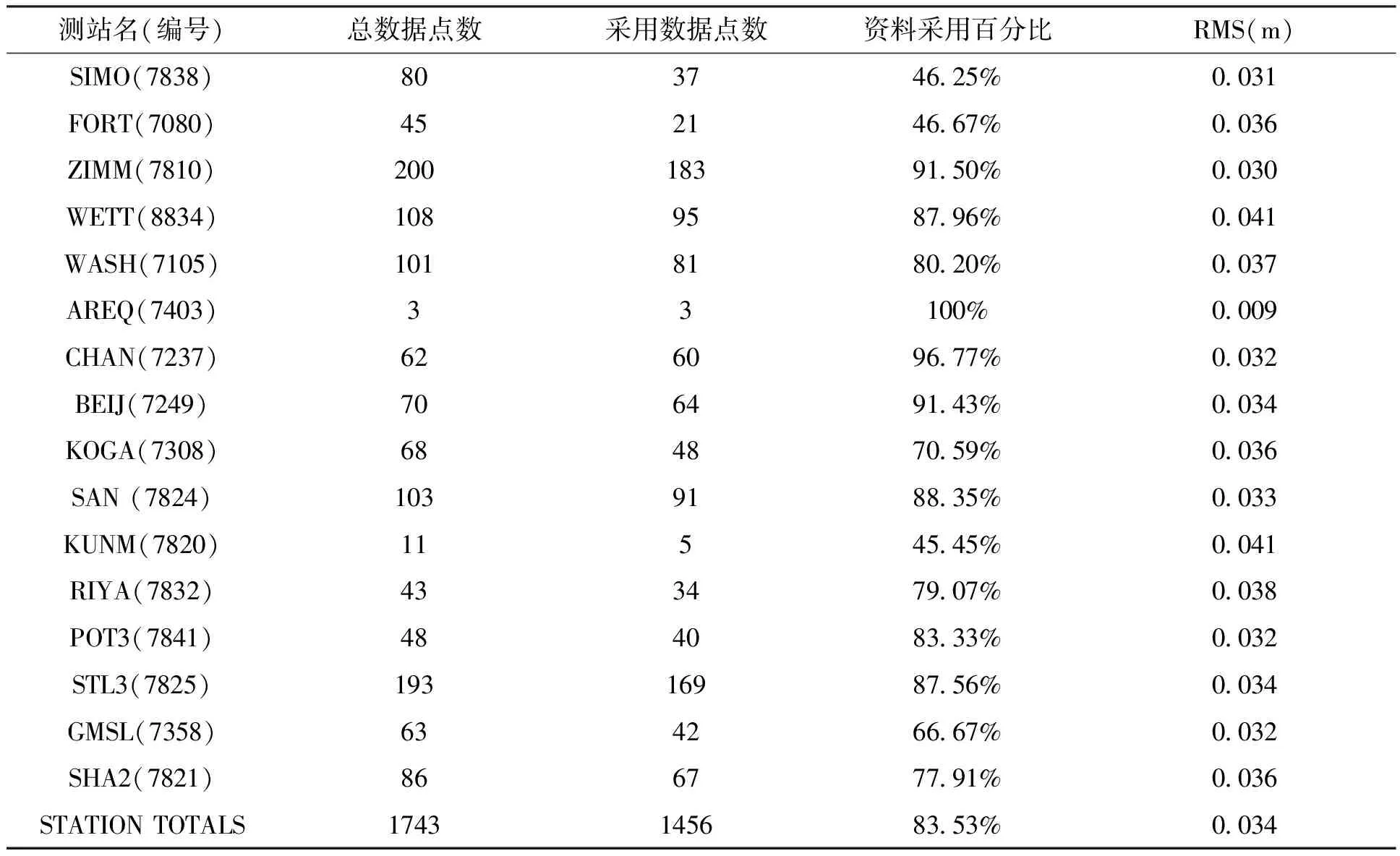
测站名(编号)总数据点数采用数据点数资料采用百分比RMS(m)SIMO(7838)803746 25%0 031FORT(7080)452146 67%0 036ZIMM(7810)20018391 50%0 030WETT(8834)1089587 96%0 041WASH(7105)1018180 20%0 037AREQ(7403)33100%0 009CHAN(7237)626096 77%0 032BEIJ(7249)706491 43%0 034KOGA(7308)684870 59%0 036SAN(7824)1039188 35%0 033KUNM(7820)11545 45%0 041RIYA(7832)433479 07%0 038POT3(7841)484083 33%0 032STL3(7825)19316987 56%0 034GMSL(7358)634266 67%0 032SHA2(7821)866777 91%0 036STATIONTOTALS1743145683 53%0 034

(2)由双行根数首次计算

表7 双行根数计算环境Table 7 The calculation evironment with TLE

由TLE起始根数得到初次轨道残差在105(m)量级，所以这里的残差判据采用105(m)。由表8可以看到估值后CD值(半天为1个弧段,3天共6个弧段)偏离了其合理值甚至变为负值，Restart一行为重置后的模型参数

表8 第1轮处理前后CD的变化Table 8 The changes of CD after the first round of calculation with TLE

两轮迭代计算的RMS变化曲线如图3、4。

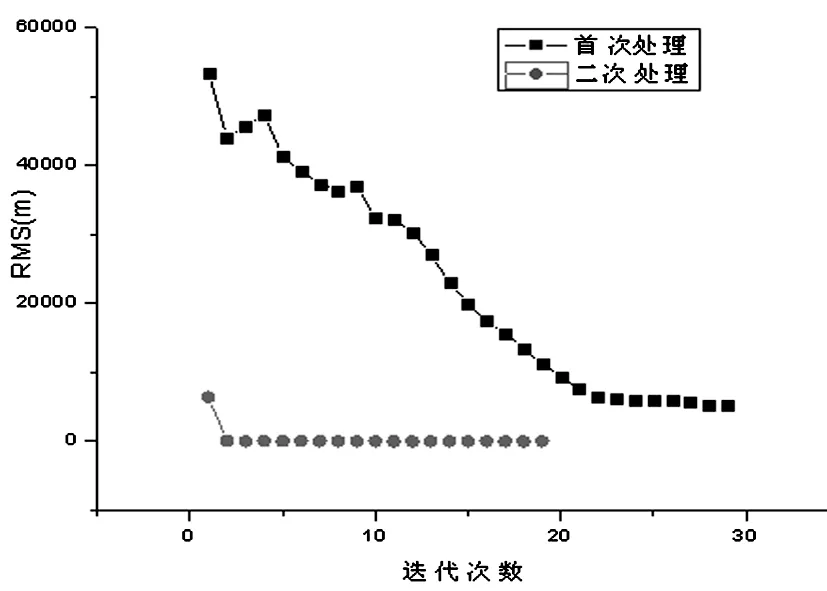
图3 TLE根数两次处理RMS比较

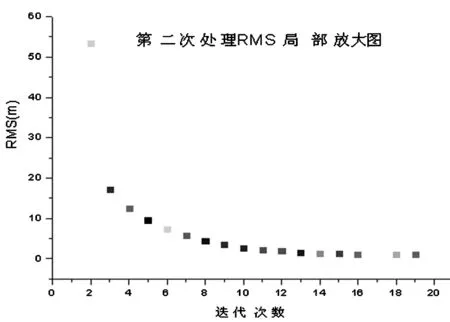
图4 TLE根数二次处理局部放大

首轮定轨计算时，在20次迭代后残差在6千米左右RMS就已经没有变化了，而此时轨道并没有达到精密定轨的精度。因为被估计模型参数中，如CD值吸收了较大的轨道初误差而偏离其合理值[5]，使得迭代次数增加而RMS数值不再减小，定轨过程没有收敛到正确结果。所以再进行第2轮计算，以首轮定轨所得状态矢量为初值并重置模型参数到其合理值范围，经过2次迭代RMS就达到了米级，这在局部放大图4 中可以清晰地看到，第2轮处理作了19次迭代计算，发现结果已经收敛到厘米级，再迭代下去RMS值不会再有新的变化，见图4。此时，多数测站的RMS已达到4至5cm，说明定轨计算过程已收敛，计算结果证明了重置参数的轨道改进算法是有效的。

图5 TLE根数作初值迭代收敛后的资料的残差分布图

第2轮处理最后一次迭代后的RMS如表9。

表9 第2轮处理RMSTable 9 The RMS errors in the second round of calculations with TLE

续 表

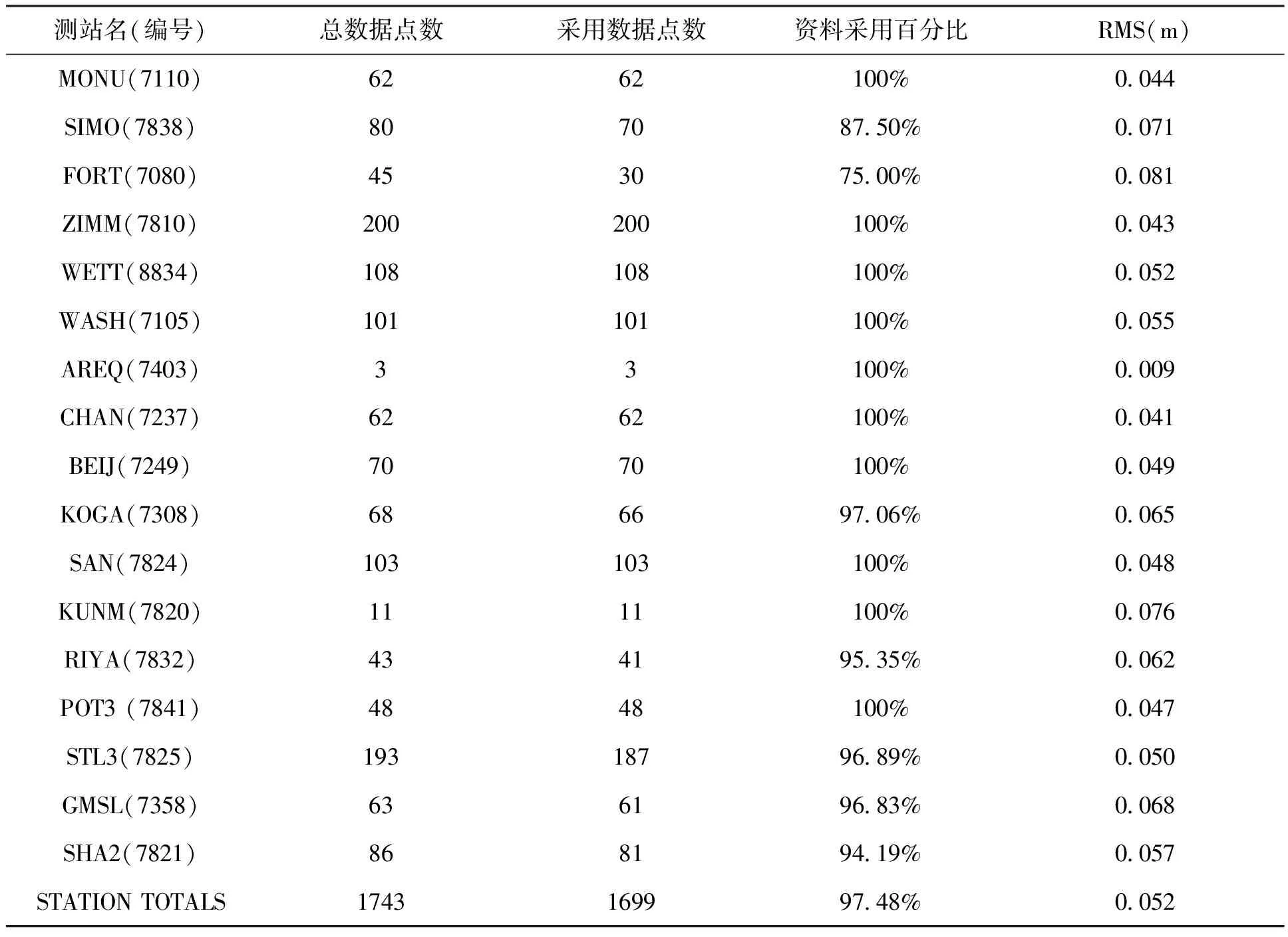
测站名(编号)总数据点数采用数据点数资料采用百分比RMS(m)MONU(7110)6262100%0 044SIMO(7838)807087 50%0 071FORT(7080)453075 00%0 081ZIMM(7810)200200100%0 043WETT(8834)108108100%0 052WASH(7105)101101100%0 055AREQ(7403)33100%0 009CHAN(7237)6262100%0 041BEIJ(7249)7070100%0 049KOGA(7308)686697 06%0 065SAN(7824)103103100%0 048KUNM(7820)1111100%0 076RIYA(7832)434195 35%0 062POT3(7841)4848100%0 047STL3(7825)19318796 89%0 050GMSL(7358)636196 83%0 068SHA2(7821)868194 19%0 057STATIONTOTALS1743169997 48%0 052

二次定轨后双行根数与精密初始根数迭代后的结果比对见表10。

表10 双行根数与SLR精密根数迭代后结果比较Table 10 Comparison of the results with TLE and SLR

由表列比较结果可知，以双行根数作为初值用上述方法进行定轨计算可以得到精密的轨道根数，表10所列计算结果位置差只有厘米级，速度差在亚毫米级。

(3)为了验证该算法的有效性，以LAGEOS-1激光卫星为算例，采用TLE根数作初值，过程同(2)最终RMS同样达到厘米级。

4 结 论

本文采用双行根数和全球激光网的SLR轨道根数作初值进行精密定轨比较计算，在初次迭代时，双行根数的残差值达到数十千米，但经过两轮数十次迭代的定轨计算，用双行根数作初值也能收敛到精密轨道上。在上述计算过程中，对模型参数的估值，如果初始根数的误差较大，某些模型参数，例如CD会吸收初始轨道中的误差，使其估值偏离合理值，定轨过程并未达到精密定轨的精度，而迭代计算的RMS值已不再变化，根数改正量变小，继续迭代也很难把轨道根数改良。而本文所用的参数重置方法则在第一轮轨道改进根数的基础上重置模型参数，再次进行迭代，这样被估值的模型参数相当于重新初始化过，使定轨计算过程收敛到正确值，达到精密定轨的目的。此方法解决了使用SLR资料进行科研时无精密初始根数的问题; 另外，此方法也可为激光漫反射空间碎片观测资料的精密定轨过程提供了算法，对空间碎片的研究具有重要意义。

[1] 韦栋，赵长印.SGP4/SDP4模型精度分析[J]. 天文学报,2009,50(3):332-339.

Wei Dong, Zhao Changyin. Analysis on the Accuracy of the SGP4/SDP4 Model[J].Acta Astronomica Sinica,2009,50(3):332-339.

[2] 刘林,周建华，马剑波. 卫星精密定轨中的数学方法[M]. 北京:解放军出版社, 2002.

[3] 彭恢全，缪元兴.一种解析定轨方法[J]. 天文研究与技术-国家天文台台刊，2007,4(4):337-342.

Peng Huiquan, Miao Yuanxing. An Analytical Method of Orbit Determination[J]. Astronomical Research & Technology,2007,4(4):337-342.

[4] Dennis D,Mdarthy，Gērard Petit.TERS conv-entions(2003).(TERS Technical Note:32)Frankfurt an Main：Verlag des Bundesamts für kartographte and Geodäsie,2004.

[5] 李济生. 人造卫星精密轨道确定[M]. 北京:解放军出版社, 1995.