关于卫星姿态确定非线性滤波算法的研究
黄 琳,荆武兴
(1.航天东方红卫星有限公司研发中心,北京100094;2.哈尔滨工业大学,航天工程系,哈尔滨150001)
0 Introduction
Spacecraft attitude determination from a sequence of vector observations in gyro-equipped spacecraft has been intensively investigated and widely applied in practice[1-2].Thequaternion is a most popular attitude representation for the global attitude estimation,though it is not a minimal representation because of its four dimensions.Various methods are proposed to keep the normalization constraint that has to be addressed in quaternion filtering problems.In general these methods can be classified as constrained estimation scheme and unconstrained estimation scheme[3-5].The former scheme assumes the quaternion estimation error covariance matrix must be singular,and the central idea is to use a nonsingular representation(i.e.,quaternion)for a reference attitude and a three-component representation for the deviations from the reference.The latter scheme assumes no such singularity and treats the four components of the quaternion as independent,but it has to incorporate some special normalization stages.More details about the two schemes and their advantages/disadvantages have been given in[3-5].
Nonlinear filtering algorithms have been used to estimate the quaternion and the gyro drift rate bias.Up to now,a number of attitude determination filters have been proposed,and some classical filters such as the multiplicative extended Kalman filter(MEKF[1]),the augmented extended Kalman filter(AEKF[6]),and the unscented Kalman quaternion filter(USQUE[7])have been widely accepted.The MEKF and the USQUE are typical constrained estimation filters,which are brought forward based on the EKF algorithm and the UKFalgorithm respectively.The AEKF is a typical unconstrained estimation filter which is proposed based on the EKFalgorithm.Recently,thesequential Monte-Carlo algorithms or the particle filtering methods[8]have been applied to spacecraft attitude determination.Cheng and Crassidis proposed a particle filter to determine the modified Rodrigues parameter(MRP)and the drift rate bias[9].However,the singularity associated with the MRP representation has to be addressed by frequently switching to an alternative set of MRPs or the quaternion,and also the ambiguity of the MRPhas to be addressed by using a so-called‘CONDMRP’solution.Moreover,the six-dimensional particle filter has to simultaneously observe several vectors and use a huge number of particles(as many as 2000,an impractical computation burden for current onboard computers).As a result,the filter is not satisfied.A different estimator is proposed by Oshman and Carmi[10],which consists of a quaternion particle filter(QPF)and a genetic algorithm(GA)embedded gyro bias maximum-likelihood estimator.The QPF is a numerical unconstrained estimator which works directly with a number of weighted quaternion particles,and it is able to completely avoid the problem of singularity.This is a remarkable advantage over the Kalman filter variants,because they have to propagate and update the quaternion estimation error covariancematrix.The quaternion ambiguity problem has also been eliminated by using a special regularization method.The bias estimation is temporarily decoupled from thequaternion estimation at each iteration.Genetic algorithms are introduced to search an optimal bias estimate from a maximumlikelihood cost function.The GA-embedded bias estimator is interlacing with the QPF,therefore the combined attitude determination filter is called by GA-QPF.The simulated results show this filter(even with 150 quaternion particles and a 200-element population for the bias estimator)can achieve a better performance with respect to several classical filters in the simulation cases where the initial quaternion estimate is uncertain.Nevertheless,the bias estimator seems sophisticated and over computing time consuming.Jiang et al propose a dual particle filter which includes an attitude particle filter and a bias particle filter[11].The proposed attitude particle filter uses two attitude representations,the quaternion and the generalized Rodrigues parameter(GRP[12]).The quaternion is used for initial quaternion particle sampling,time propagating,observation updating,and particle resampling,while the GRPis used for the computations of the mean and the covariance matrix and the rougheing of the resampled particles.A similar idea has been given in[9]also.However,the GRP ambiguity problem has been ignored in[11].The bias particle filter is the direct application of astandard particle filter(i.e.,bootstrap filter).Jiang et al[13]proposed a marginalized particle filter for spacecraft attitude determination,by applying the Rao-Blackwellisation technique to an approximated quaternion and bias estimation,where the bias vector is partitioned from the augmented state of quaternion and bias and assumed to be conditionally linear Gaussian.Therefore the used bias estimator is a Kalman filter in nature.However,the model approximation of the original nonlinear/non-Gaussian attitude determination problems destroy the normalization constraint of the quaternion propagation,and its uncertain influence has not been considered and investigated.Once again,the GRPambiguity problem has not been eliminated in this work.
This paper proposes two novel attitude determination filters for a low-Earth satellite with a three-axis magnetometer(TAM)and a three-axis gyro(TAG).The two filters are modified from the GA-QPF and the DPF[11].Both filters take the QPF as their quaternion estimator,so that the frequent switching between the GRP and the quaternion is avoided for the particle attitude filter of[11],whereas the QPF given in this paper uses a slightly different quaternion particle resampling and regularizing methods.The main difference between the twofilters is using different bias estimators.Onefilter uses an auxiliary particle filter,which is believed to be capable of resolving the state filtering problems with small process noise better than the bootstrap filter[8].The other uses a UKFwhich is believed to be an appropriate algorithm for the gyro bias estimation of approximately Gaussian distribution and also for its low amount of calculation.Hence the two novel filters are named of the modified DPF and the HFrespectively.
1 Gyro-equipped attitude determination state space models
A general continuous dynamics model is given in[1-2],which in general is discretized as[2,7]
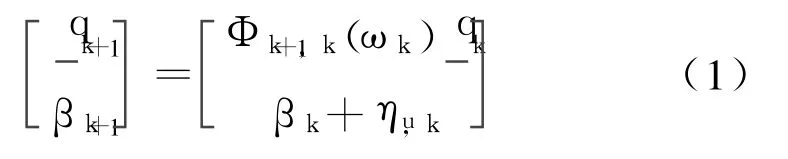
whereqkis the quaternion,q =[qTq4]T,q is the vector part and q4is the scalar part.βkis the TAGdrift rate bias vector;is a stationary zero-mean,white noise process with covariancewhereinis an orthogonal transition matrix about the true angular velocityωkof the body(B)frame with respect to the reference(R)frame,(ωkis resolved in B frame.)and the matrix is given
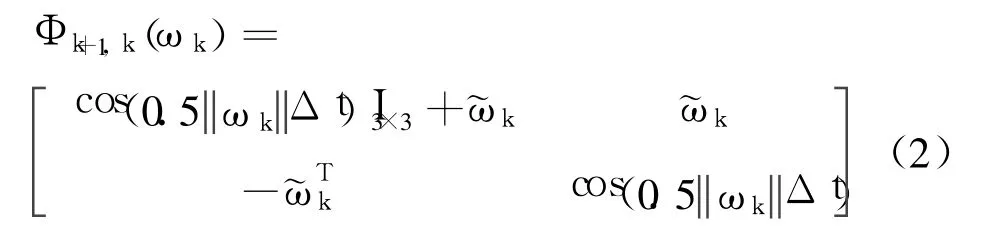
the true rateωkis unknown and is obtained from the TAG measurement,whereinis the TAG measurement,ηυ,kis the zero-mean white Gaussian measurement noise with covarianceThe TAM vector observation model is given[2]

where~bkis the TAMmeasurement,bR,kis the reference geomagnetic field,vB,kis the TAM observation noise whose distribution is already known,Akis the attitude matrix of the B frame with respect to the R frameand is the matrix representation of the quaternion qk.
2 Modified dual particle filter
In this section,first the present quaternion particle filter which is slightly different from the QPF is simply introduced,then an auxiliary particle bias filter is completely given.Consider the resamplingand regularizing disturb the posterior representation[8],it is better for the precision with a posterior estimation to implement the computations of the mean and the covariance before the resampling and regularizing stage.
2.1 Quaternion particle filter
2.1.1 Initialization(k=0)
A single vector observation can not make the threedimensional attitude completely observable,though the rest uncertain attitude information is reduced to one dimension,i.e.,the rotation angle around the vector.Oshman and Carmi make use of the fact and propose a method to generate a number of initial quaternion parti-cles(or samples)which keep the normalization constraint.A detailed technique is presented in Appendix B of[10].However,the choice of an appropriate number of initial quaternion particles denoted by NSdepends on simulation experience.Denote the initial prior quaternion particle set byand the corresponding weight set byClearly,
2.1.2 Observation update(k=0,…,N)
Firstly calculate the likelihood probability of the quaternion particle
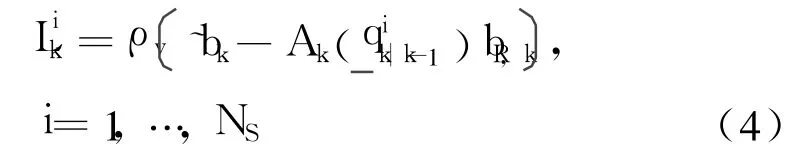
whereρv(·)represents the probability density of the observation noise vB,k.
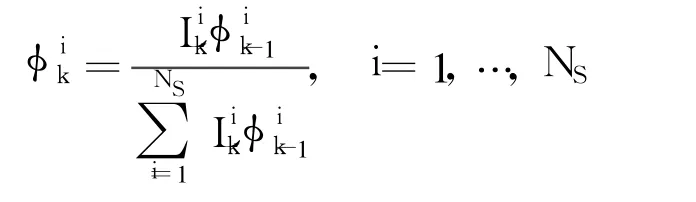
2.1.3 Computation of mean and covariance(k=0,…,N)
The application of the classical solutions to compute the mean and the covariance from the weighted particle set to the weighted quaternion particles may destroy the normalization constraint and get in trouble with the quaternion ambiguity problem.One maximumposterior probability(MAP)approach and two minimum mean square error(MMSE)approaches are recommended in[10]to compute the mean quaternion.Consider a low accuracy of the MAP approach and the identical character of the two MMSE approaches,this paper only uses the second MMSE approach that is similar to Davenport’s well known‘q-method’.The optimal quaternion estimateis the normalized eigenvector corresponding to the largest eigenvalue of matrix

where tr(·)is operation of‘trace’,matrix Bkand vectorζare respectively defined by
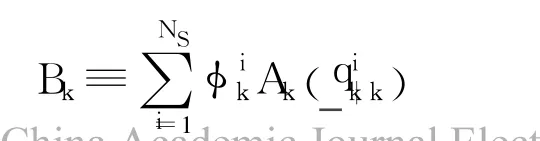

The quaternion estimation error covariance is given[10]

2.1.4 Resample and regularization(k=0,…,N)Calculate the effective sample size

Denote the 3×3 matrix of the vector part of the quaternion estimation error covariancebyand its square root matrix bythen draw samples as


wherein N(·|m,S)is a multivariate normal density with mean mand variance S;hGis the bandwidth of the Gaussian kernel and is suggested with the optimal value
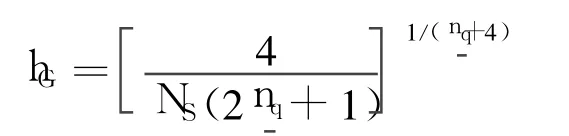

Finally,the diversity of the resampled quaternion particles is added as
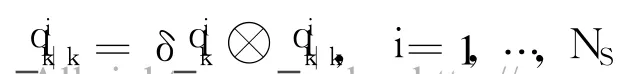
2.1.5 quaternion particle propagation(k=0,…,N)
The TAG sample periodΔh is much smaller than the TAM sample periodΔt.Assume the two periods satisfy KRIG=Δt/Δh,where KRIGis an integer.The quaternion particle is propagated by using
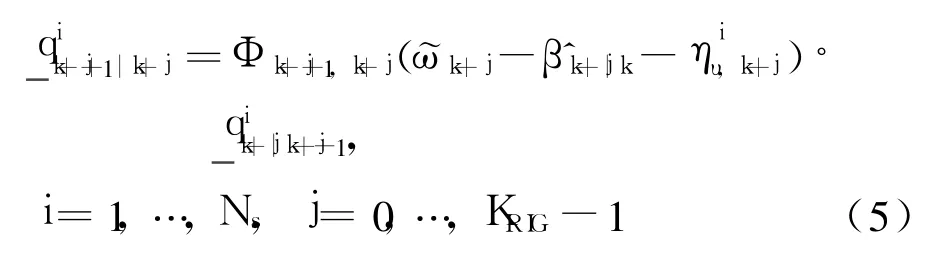
2.2 Auxiliary particle bias filter
Based on the standard particle filter(e.g.,bootstrap filter),Pitt and Sheppard[14]proposed a socalled auxiliary particle filter that is able to automaticly generate particles from the particles of the previous time step which are most likely to the true state.Compared to the bootstrap filter,this filter is effective to deal with state filtering problems when the process noise is small.Consider that the process noiseηu,kis small for the bias vectorβk,one can see the auxiliary particle filter is a better bias estimator.
2.2.1 Initialization(k=0)
Draw initial aprior bias particles from the prior distributionρ(θ0),say,a Gaussian distribution
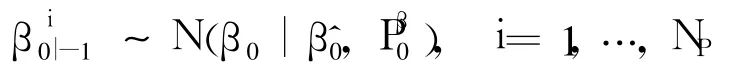
whereβ^0andare the initial bias mean estimate and covariance estimaterespectively.Denote theinitial aprior bias particleset by
and their corresponding weight set by.Clearly,Calculate the initial likelihood probability
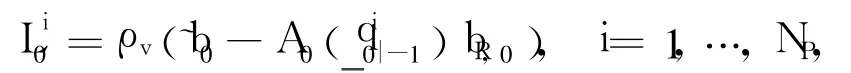
where the NPinitial quaternion particlesmight be chosen from the generated initial quaternion particleOf course,this is for the case where NP≤NS.Otherwise,theextra NP-NS+1quaternion particleshave to be additionally generalized.In this paper,assume NP=NS.Finally,calculate the weightsand normalize them as

2.2.2 Bias particle propagation(k=1,…,N)
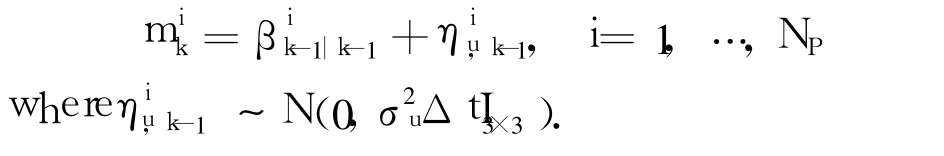
Secondly,calculate the likelihood probability of some biasby using a similar method as Eq.(4)
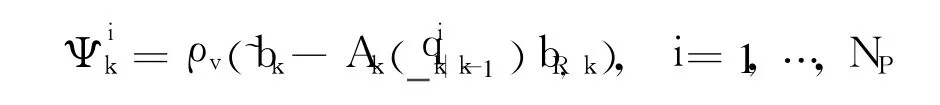
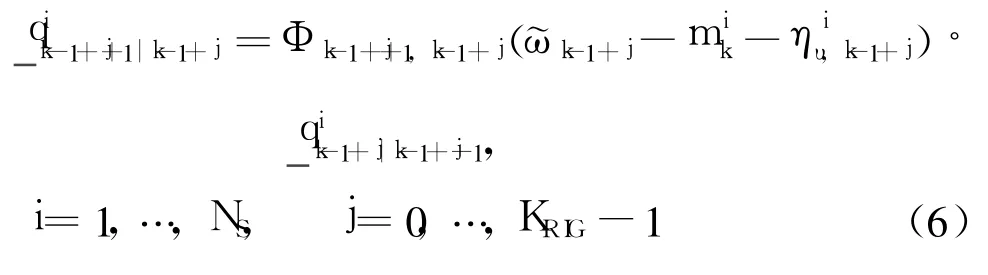
Thirdly,calculate the weightsand normalize them as

select the high likely bias particles of previous time step using the systematic resample method,e.g.,

where il represents the current particle‘l’is drawn from the particle‘i’of previous time step.
Finally,the bias particles are propagated as
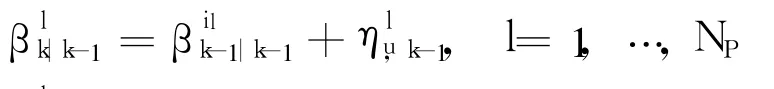
2.2.3 Observation update(k=1,…,N)
Firstly,calculate the likelihood probability again
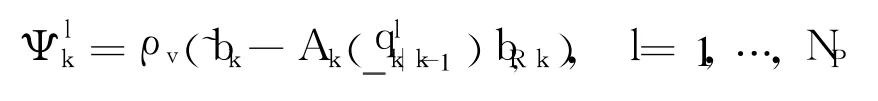

2.2.4 Computation of Mean and Covariance(k=0,…,N)
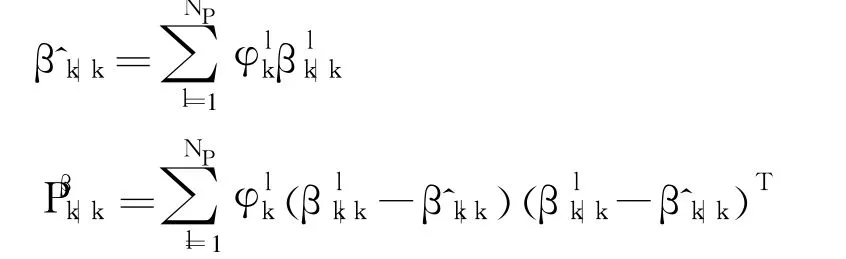
2.2.5 Resample and regularization(k=0,…,N)
This step is believed to be unnecessary for an auxiliary particle filter by Arulampalam et al[8],but improved by Pitt and Sheppard[14].This paper suggests taking this step when the effective sample sizeis below given threshold,e.g.,2NP/3.The weights of the resampled bias particles are set to1/NP.Regularize the resampled bias particles as follows


3 Hybrid filter
The difference of the HFfromthe modified DPFis the use of a UKF bias estimator,which is a direct application of the UKF algorithm to the 3-dimensional bias estimation.The bias UKF is given as follows.
3.1 Initialization(k=0)
Denote theinitial aprior mean estimate and covariance estimateandto generate a initial bias sigma point setthe weights for calculating the mean and the covariance are denoted byandrespectively.
Then choose seven initial aprior quaternion particles from the setand generate seven prediction observation sigma points as
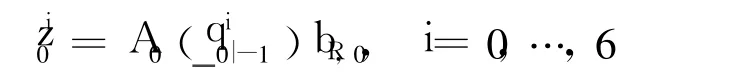
3.2 Observation update(k=0,…,N)
Firstly,calculate the mean observation
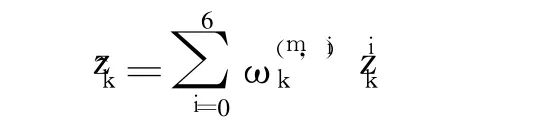
Secondly,calculate the innovation and its covariance respectively

where Rkis the covariance of the observation noisevB,kwhich is regarded as a zero-mean,white Gaussian noise.
Thirdly,calculate the correlative covariance matrix and the gain matrix respectively
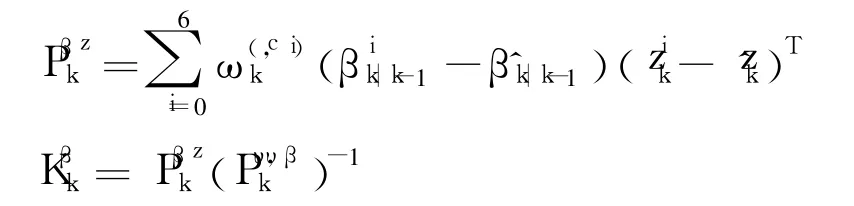
Finally,calculate the posterior mean and covariance respectively

3.3 Bias sigma point propagation(k=0,…,N)
Firstly predict the bias mean and the covariance matrix
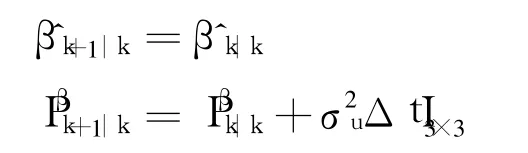
Then generate prediction observation sigma points as
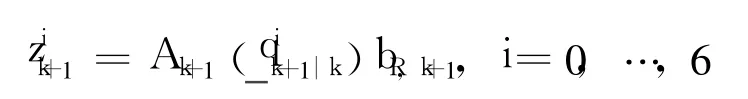
where
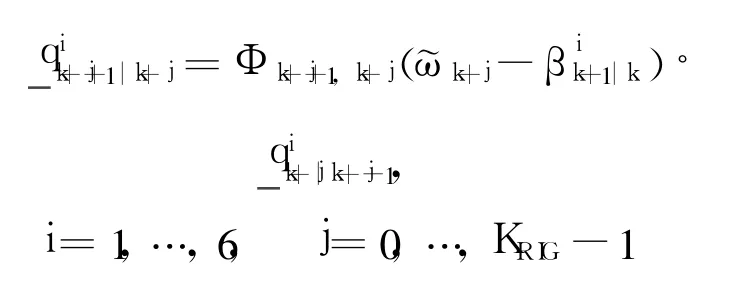
4 Simulation results and analysis
A typical small satellite considered in[15]is chosen in the simulation section.The satellite runs in a nearly circular low Earth orbit with an inclination of 82°and a height of 823 km,it is out of control and spinning with an initial rate of 2.0°/s.The real geomagnetic field vector is simulated using a 10-order international geomagnetic reference field model.The reference vector is simulated using an 8-order model.White and colored TAM measurement noise processes are considered.The white Gaussian noise of 60 nT(σ)is used in the simulations of subsections 4.1 and 4.2,and the colored noise is introduced to the simulations of subsection 4.3.The colored-noisemodel is described by a first-order Markov process driven by white noise[16].The‘time constant’of the Markov process has been chosen corresponding to an orbital arc length of 18°(about 300 s in this paper).The power spectral density of the white-noise driving term has been chosen,so that the magnitude of the colored noise will match the white Gaussian noise used in subsections 4.1 and 4.2.The measurements periodΔt of the TAM is 10s.The TAG output is contaminated with a measurement noise with two components:a white zero-mean Gaussian process with intensityand a drift bias modeled as an integrated Gaussian white noise with intensitys3.The true initial drift rate bias is set to 0.1°/h on each axis.The sampling periodΔh of the TAG is 1s.
4.1 Effects of various particle numbers on performances of the modified DPF and the HF
Various particle numbers are chosen to test the performances of the modified DPF and the HF.For convenience,let NP=NS.The initial bias mean estimate and the covariance estimate are given
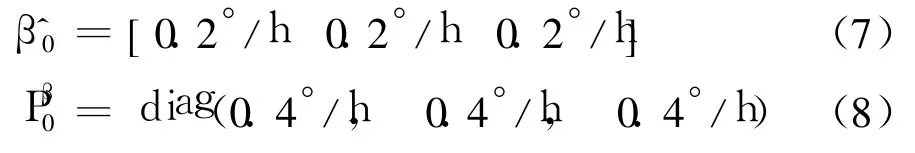
To evaluate thequaternion and the bias filtering errors,two indexes used in[10]are introduced.One is for the quaternion estimation error(in degrees)evaluation and is given

whereδq4is the scalar component of the error quaternionδq.The other is the TAGbias estimation error norm(in°/h).
The time histories of the quaternion estimation errors of four HF filters(NSP=120,NSP=300,NSP=600 and NSP=900)show the steady-state estimation errors are not more than 0.25°and the differences among them are slight.These HF filters converge from large initial errors(>150°)into the steady-state errors in about 10min.Similar results are obtained from the modified DPF.However the bias estimation errors of the modified DPF filters and those of the HF filters shown in Fig.1 are different.Fig.1a shows the bias errors of the HF filters always remaining in the neighborhood of some constant bias during the whole time interval.Fig.1b shows that the errors of the modified DPF filters first increasing and then remaining in the neighborhood of some constant bias.By far it is not difficult to find that the effects of particle numbers on the attitude and bias filtering performances of the two novel filters are not very crucial or clear when 900≥NS=NP≥120.Therefore,in the following simulations,NS=NP=120 are used.
In addition,a large initial bias estimate is used to test the convergent performance of the HF,e.g.,
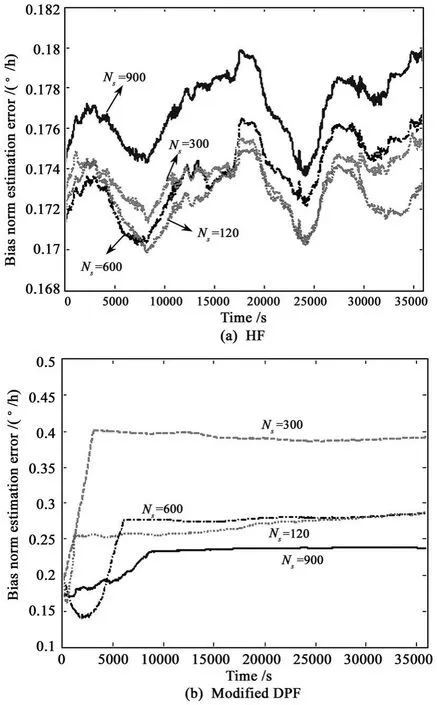
Fig.1 Bias norm estimation errors of modified DPF and HF with various numbers of particle
However,it takes the HF about 11h to reach the steady-state attitude estimation error of 0.25°,and the bias norm estimation error indeed decreases to a nearly constant rate.As shown in Fig.2,the slow rate does not mean the bias UKFis an inefficient filter in nature.The real reason,we suspect,is that the innovated information from the vector observations can not be directly fed back to the observation updating of the bias estimate.Unless mentioned,the initial bias estimate used in the simulations is better estimated as given in Eqs.(7)and(8).
4.2 Effects of initial quaternion estimate on filtering performances
The two novel filters have been compared to the MEKF and the USQUE.Different initial quaternion estimates have been considered for the MEKF and the USQUE,while the modified DPF and the HF generate the initial quaternion particles using the technique in Appendix B of[10].
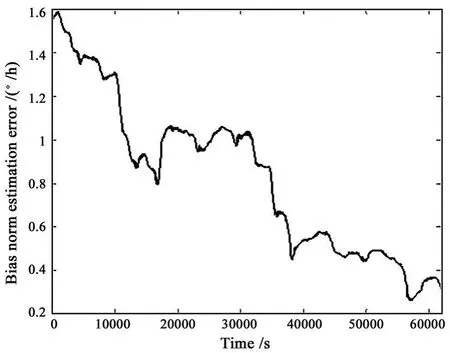
Fig.2 Bias norm estimation errors of HF with a bad initial bias estimate
4.2.1 Constant initial quaternion of small estimation error
In this example,an initial quaternion estimate whose norm attitude error is 50°has been chosen for the MEKF and the USQUE.A large initial attitude covariance matrix has been chosen for the MEKF and the USQUE.Though the large matrix might be physically meaningless,it can speed up the convergence.
The results show that the four filters converge to the steady-state quaternion estimation errors at almost same rate and their quaternion estimation errors are of same level.However,the MEKF and the USQUE reach their bias estimation errors equivalent to HF in about 10000 s and the errors of all the three filters are lower than the modified DPF almost during the whole time interval,as shown in Fig.3.
Obviously,the classical filters can achieve a better performance with much less calculation when the initial quaternion estimation error is small.If a good initialization is expectable,either the MEKFor the USQUE is a more promising filter.
4.2.2 Constant initial quaternion of large estimation error

Fig.3 Bias norm estimation errors of four filters with constant initial quaternion estimate(small-error case)
In this example,a worse initial quaternion estimate whose norm attitudeerror is 160°has been chosen for the MEKF and the USQUE.Compared to those above results,the modified DPF and the HF keep almost same performances,whereas the performances of the other two classical filters sharply degenerate and are much worse than the two novel filters.Fig.4 shows that,the novel filters reach the quaternion estimation error of less than 0.25°in about 10 min,whereas the USQUE and the MEKF need about 17 h respectively to reach the errors of less than 0.5°and 1.5°.Obviously the modified DPF and the HF are more promising when the initial estimation error is large.Necessary to mention,thebetter performance of the USQUEwith respect to that of the MEKF is obtained by regulating the UT parameter(i.e.,α∈[0,1]).That is to say,the same USQUE does not guaranteed in any case to achieve a steady performance than the MEKF.In other words,the classical filters depend more on the regulating work than the novel filters do.

Fig.4 Quaternion estimation errors of four filters with constant initial quaternion estimate(large-error case)
4.2.3 Uncertain initial quaternion
In this part,the initial quaternion estimates of the MEKF and the USQUE are ramdomly generated according to a uniform distribution on the unit hypersphere.The four filters are executed independently for 50 Monte Carlo runs.The maximum errors of the four filters during 30000 s to 62000 s are chosen for each run.The statistical distribution results of these maximum errors are given in Table 1.One can see that,the HF in 50 runs all reaches the quaternion estimation error of less than 0.5°.The convergent performance of the modified DPF is a little worse than HF but much better than the USQUE,The MEKF is the worst.
In addition,the average runtimes of the four filters are also tested.The results can be regarded as an indirect evaluation of their average calculation amounts.The 50×4 runs are executed in the computers of same computing capacity.If denote the average runtime of the MEKF as 1,then the USQUE,the HF,and the modified DPF are 6,60,and 170 respectively.Surprisingly,the HF filter’s runtime is only 10 times as the USQUE filter’s.So the HFis a promising filter for onboard applications.

Table 1 Statistical distribution results of quaternion estimation errors of four filters with uncertain initial quaternion estimates(50 runs)
4.3 Effects of colored observation noise on filtering performances
In this example,the performances of the four filters using colored TAM measurements have been tested.Use the third innovation(i.e.,residual)component processes of the MEKF,the USQUE,the modified DPF,and the HF respectively for the white noise and the colored noise,an exact evaluation is done by computing the time-averaged autocorrelation[17]
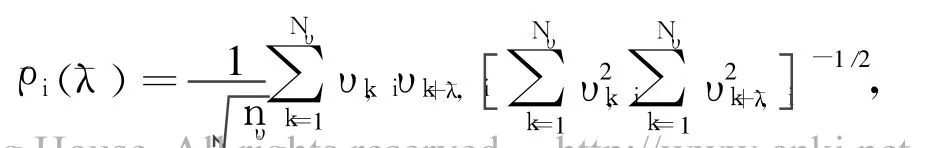
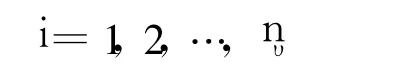
whereυk,iis the ithcomponent of the innovation vector at timetk;¯λis the correlative step;nυis the dimension of the innovation vector;Nυis the number of the considered observation data points.If the innovation process is zeromean white Gaussian,the¯ρi(¯λ)is zero mean with variance of 1/Nυfor Nυlarge enough.In this example,Nυ=4000and various¯λare used.The mean and variance results of¯ρi(¯λ)for the white noise and the colored noise are respectively given in Table 2and Table 3.For an optimal filter,the mean and the varianceof¯ρi(¯λ)should be 0 and 2.5×10-4respectively.Table 2 shows that the mean results for the four filters are comparable and close to zero,whereas thevarianceresults for themodified DPF and the HF are considerably close to the optimal values and thevarianceresults for the two classical filters are far from the optimal values.That is,the novel filters can process the vector observations with white noise much better than the classical filters do.Similar conclusions can be drawn from the results shown in Table.3.Comparing Table 3 to Table 2,one can see the variance values for the two novel filters which use thecolored observations have increased many times,while those for the classical filters appear no remarkable varieties.

Table 2 Statistical results for time-averaged autocorrelation indexes of four filters’residuals(the third component)in the white-noise case

Table 3 Statistical results for time-averaged autocorrelation indexes of four filters’residuals(the third component)in the colored-noise case
5 Conclusions
Two novel filters are proposed for the gyro-equipped spacecraft attitude determination from vector observations.They are modified DPF and HF respectively.Both filters consist of same quaternion particle filter but use a different gyro drift rate bias estimator.The modified DPF filter uses an auxiliary particle bias filter,while the HF filter uses a UKF bias filter.An extensive simulation study has been done to evaluate the performances of the two novel filters and tocompare them with two classical filters:the MEKF and the USQUE.
Several important conclusions are drawn.The first is,none of the considered filters can always achieve a best estimation performance in any case.The classical filters can achieve better estimation accuracy with respect to the two proposed novel filters with much smaller computing amounts when a good initial quaternion estimate is expectable;otherwise their convergent performances are possibly reduced and even much worse than those of the novel filters,whereas the proposed filters are able to achieve the consistent estimation performances in various cases.Thesecond is,theeffect of the particle number on the estimation performance of the modified DPF or the HF is not very crucial when the number is large enough.Surprisingly,both the HF and the modified DPF can achieve a better convergent performance with only 120 particles.The HF is a promising filter for the real-time spacecraft attitude de-termination applications.The third is,the novel filters can process the vector observations much better than the classical filters do.All considered filters show some certain robustness for colored vector observations.At last,an advice that has been made by someone else is repeated again,that is,thecombined use of theclassical Kalman filter variants and the recently proposed particle attitude determination filters is likely to achieve a better estimation performance.For example,the HF is used as an initialization stage for the MEKF or the USQUE.
[1] Lefferts E J,Markley F L,Shuster M D.Kalman filtering for spacecraft attitude estimation[J].Journal of Guidance,Control,and Dynamics,1982,5(5):417-429.
[2] Markley F L,Crassidis JL,Cheng Y.Nonlinear attitude filtering methods[C].AIAA Guidance,Navigation,and Control Conf.and Exhibit,SA,California,USA,Aug.,2005.
[3] Shuster M D.Constraint in attitude estimation part I:constrained estimation[J].The Journal of the Astronautical Sciences,2003,51(1):51-74.
[4] Shuster M D.Constraint in attitude estimation part II:unconstrained estimation[J].The Journal of the Astronautical Sciences,2003,51(1):75-101.
[5] Markley F L.Attitude estimation or quaternion estimation[J].The Journal of the Astronautical Sciences,2004,52(1-2):221-238.
[6] Bar-Itzhack I Y,Oshman Y.Attitude determination from vector observations:quaternion estimation[J].IEEE Trans.on Aerospace and Electric Systems,1985,21(1):128-136.
[7] Crassidis JL,Markley FL.Unscented filtering for spacecraft attitude estimation[J].Journal of Guidance,Control,and Dynamics,2003,26(4):536-542.
[8] Arulampalam M S,Maskell S,Gordon N,Clapp T.A tutorial on particle filters for online nonliear/non-gaussian bayesian tracking[J].IEEE Trans.On Signal Processing,2002,52(2):174-188.
[9] Cheng Y,Crassidis J L.Particle filtering for sequential spacecraft attitude estimation[C].AIAA Guidance,Navigation,and Control Conf.and Exhibit,Rhode Island,USA,Aug.,2004.
[10] Oshman Y,Carmi A.Attitude estimation from vector observation using genetic-algorithm-embedded quaternion particle filter[J].Journal of Guidance,Control,and Dynamics,2006,29(4):879-891.
[11] Jiang X Y,Ma G F.Spacecraft attitude estimation from vector measurements using particle filter[C].The 4th Intel.Conf.on Machine Learning and Cybernetics,Guangzhou,China,Aug.,2005.
[12] Schaub H,Junkins JL.Stereographic orientation parameters for attitude dynamics:ageneralization of the rodrigues parameters[J].The Journal of the Astronautical Sciences,1996,44(1):1-19.
[13] Jiang X Y,Ma G F.Satellite attitude estimation based on marginalized particle filter[J].Control and Decision,2007,22(1):39-44.
[14] Pitt M,Shephard N.Filtering via simulation:auxiliary particle filters[J].J.Amer.Statist.Assoc.,1999,94(446):590-599.
[15] Psiaki M L.Global magnetometer-based spacecraft attitude and rate estimation[J].Journal of Guidance,Control,and Dynamics,2004,27(2):240-250.
[16] Alonso R,Shuster M D.TWOSTEP:a fast robust algorithm for attitude-independent magnetometer-bias determination[J].The Journal of the Astronautical Sciences,2002,50(4):433-451.[17] Bar-Shalom Y,Li X R,Kirubarajan T.Estimation with applications to Tracking and Navigation[M].New York:John Wiley&Sons,Inc.,2001.
- 宇航学报的其它文章
- 卫星编队飞行姿态协同输出反馈控制

