洪水灾情评价的脉冲耦合神经网络模型*

杨聪辉，王宝华，付强，谢永刚

(1.广州市水利水电勘测设计研究院，广东广州510640;2.东北农业大学水利与建筑学院，黑龙江哈尔滨150030;3.黑龙江大学生产力研究中心经济与工商管理学院，黑龙江哈尔滨150080)

洪水灾情评价，就是根据洪水灾情评价标准和各评价指标值，对因洪水灾害造成的破坏程度进行综合评估，灾情评价的结果(灾情等级)对洪水灾害的分类管理具有重要的指导意义［1－2］。洪水灾情评价涉及自然环境与社会经济等众多因素，目前国内外尚没有统一的洪水灾情评价指标体系和对各指标的灾情等级评价标准，因此，这至今仍是洪灾研究的难点和热点之一［1］。在洪水灾害损失评价方面相继提出了灾度判别法、模糊综合评判、物元分析、传统的BP模型等灾情等级模型［2－11］。但是，灾度判别法、模糊综合评判、物元分析法在确定权重时或多或少地存在着主观人为因素的影响和函数模式类评价方法构造评价指标集与评价等级之间函数关系的困难;传统的BP模型虽然克服了权重的主观因素，但传统的BP模型等灾情等级模型要构建训练网络，经过不断的学习训练权值、阈值，直至网络全局误差函数小于预先设定的一个极小值，然而权值、阈值同时训练网络还存在着训练次数大，易陷入局部最优，网络不宜收敛的缺点［12］。上述方法在解决洪水灾情评价这一类评价指标与洪水灾害等级之间复杂的非线性关系的问题中都不是十分理想。

近年来，被国际上称为第三代人工神经网络的脉冲耦合神经网络(PCNN)以其更接近生物机制的优越性，被广泛地应用在图像处理、决策优化和通信等方面［13］。因该方法通过脉冲输出从而调节阈值，并且应用动态阈值来确定洪水灾情的等级，比传统的BP模型简化了权值的训练。脉冲耦合神经网络模型更加简便、直观的特点将其应用领域推广到洪水灾情评价中是一次新尝试。

1 PCNN模型结构

脉冲耦合神经网络(Pulse Coupled Neural Networks，PCNN)是近十余年在国内外兴起的新型神经网络，国际上称PCNN为不同于传统神经网络的第三代人工神经网络。2000年Bressloff和Coombes［14］对具有强耦合的PCNN的动态行为进行了研究，指出在弱耦合情况下稳定的相位锁定状态是如何随着耦合强度的增加而进入不稳定的。并由此发展形成了PCNN模型。该模型是新兴起的其应用领域必将越来越广泛，理论也越来越完善。PCNN模型在洪水灾害评价中的应用还是空白，本文提出了该模型在洪水灾情评价中的应用。

PCNN的单个神经元模型［15］由接收域、调制部分和脉冲产生部分三者组成，大致结构见图1。

接受域:接受域接收来自其它神经元与外部的输入。接受域接收到输入后，将其通过两条通道传输。其中，一条通道称为L通道(式(1))，另一通道称为通道(式(2))。

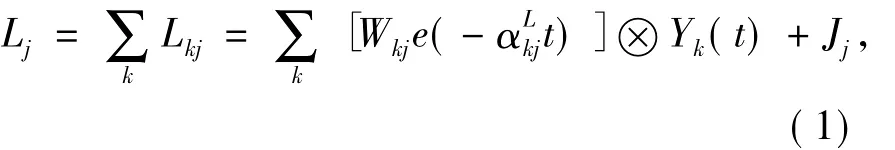
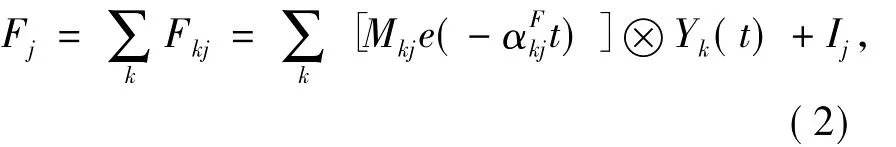
式中:Wkj与Mkj为突触联接权;数;Jj与Ij为输入常量;Yk(t)为神经元点火与否的信息。

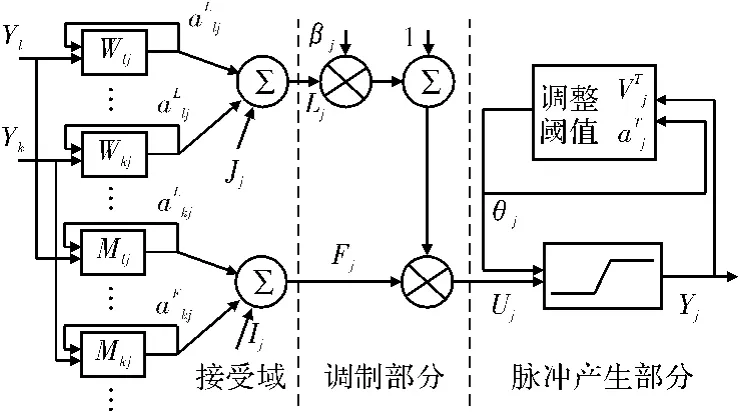
图1 PCNN单个神经元的模型

调制部分:调制部分将来自L通道的信号Li加上一个正的偏移量后与来自F通道的信号Fi进行相乘调制，见式(3)，模型中偏移量归整为1。

式中:Uj为相乘调制得到的信号;βj为联结强度。

脉冲产生部分:由阈值可变的比较器与脉冲产生器组成。当脉冲产生器打开时，其发放脉冲的频率是衡定的。当神经元输出一个脉冲，神经元的阈值就通过反馈迅速得到提高。当神经元的阈值θj超过Uj时，脉冲产生器就被关掉，停止发放脉冲。接着，阈值就开始指数下降，当阈值低于Uj时，脉冲产生器被打开，神经元就被点火，即处于激活状态，输出一个脉冲或脉冲序列。由此可知，神经元输出脉冲的最大频率不能超过脉冲产生器产生脉冲的频率。

从PCNN的结构中可以看出，神经元的输出为脉冲，来自其它神经元的输入亦为脉冲;构成PCNN的神经元的阈值是随着时间改变的，同时受到神经元输出的影响;PCNN中的神经元是先分别求输入信号与F通道和L通道的脉冲响应函数的卷积和，然后再进行相乘调制，调制结果与阈值相比，得到输出。PCNN模型连接输入部分等于上一次点火时的脉冲，直接体现了前后神经元之间的联系;并且应用动态阈值来确定洪水灾情的等级，这样调节阈值更容易对样本进行分类;省略了传统BP模型中权值的训练，减少了模型的复杂度。

2 基于PCNN模型在洪水灾情评价中的应用

2.1 PCNN计算步骤

PCNN根据应用不同，所采用计算公式不同，PCNN在洪水灾情评价中的步骤如下。

步骤1:对自然灾害等级和单指标分级标准单位数量级归一化处理。设自然灾害等级和单指标分级标准为{［a(i，j)，b(i，j)］，i=1，2，…，ni，j=1，2，…，pj}，其中a(i，j)，b(i，j)分别为第i级灾情第j个评价指标变化区间的上限值和下限值，j为第i级灾情标准的等级数目，ni、pj分别为洪水灾情标准的等级数目和评价指标数目。为消除各上下限值的量纲和统一各限制的变化范围，可采用下式进行极值归一化处理，例如对于越小越优的指标［16］:

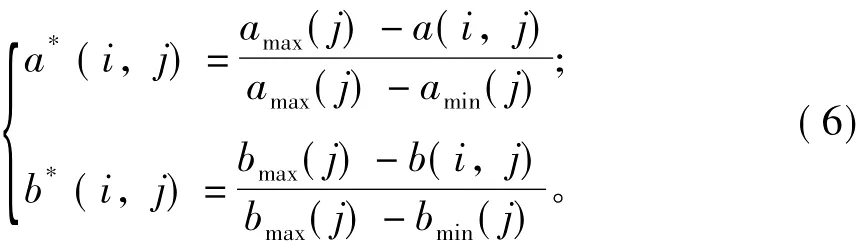
步骤2:利用均匀随机数在各级指标变化区间［a*(i，j)，b*(i，j)］内随机产生的25个指标样本值x(k，j)，相应的标准等级值y(k)=i。这样就得到了洪水灾情评价标准样本系列{x(k，j)，y(k)，k=1，2，…，nk，j=1，2，…，nj}，其中nk为样本容量。在步骤1中上下限值已经进行了归一化处理，因此评价标准系列不必再进行归一化处理。

步骤3:设初始连接部分的连接权和阈值均为0，VL为连接幅度系数，取值1，Ykl(n－1)为神经元x(k，j)点火与否的信息。采用F通道计算:

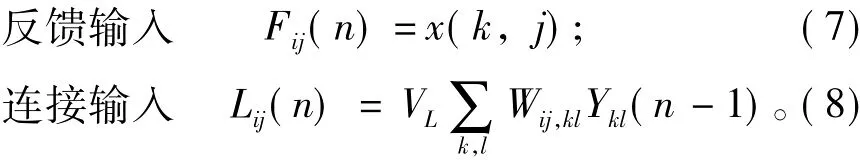
步骤4:调制部分。反馈输入和连接输入经过调制部分的作用产生神经元x(k，j)的内部活动项:

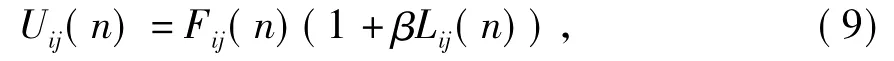
式中:β为连接强度取值0.01，神经元x(k，j)的脉冲生成器根据内部活动项Uij(n)的一个阶跃函数产生二值输出，并根据神经元x(k，j)点火(激活)与否的状态自动调整阈值θij的大小。如果神经元x(k，j)点火，则对θij进行调整:

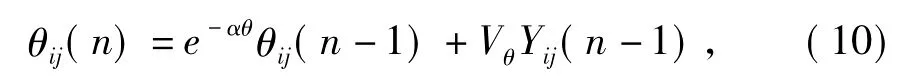
式中:αθ为时间衰减常量;Vθ为阈值常量。

步骤5:脉冲产生部分。

在该简化模型中，活动阈值θkj代表评价指标的标准，运行模型进行评价只需考虑阈值的情况，用阈值控制模型的输入等级。当Yij(n)=1时则神经元x(k，j)点火(激活)，则输出评价等级值。

2.2 实例应用

(1)基本资料:以新疆“96.7”洪水灾害中6个城市的灾情评价为例进行实例分析(表1)。受灾面积主要是指农作物受灾面积(包括农作物成灾面积和农作物绝收面积)和毁坏耕地面积两大部分(hm2);受灾人口指因洪水而受灾的人口(人);破坏房屋包括损坏房屋和倒塌房屋两部分，以受灾面积作为分级依据(m2);直接经济损失指由洪水灾害造成的直接经济损失(元)。4个评价指标将新疆“96.7”洪水灾害灾情划分为极重灾、重灾、中灾、小灾、微灾5个等级［17］，评价标准见表2。

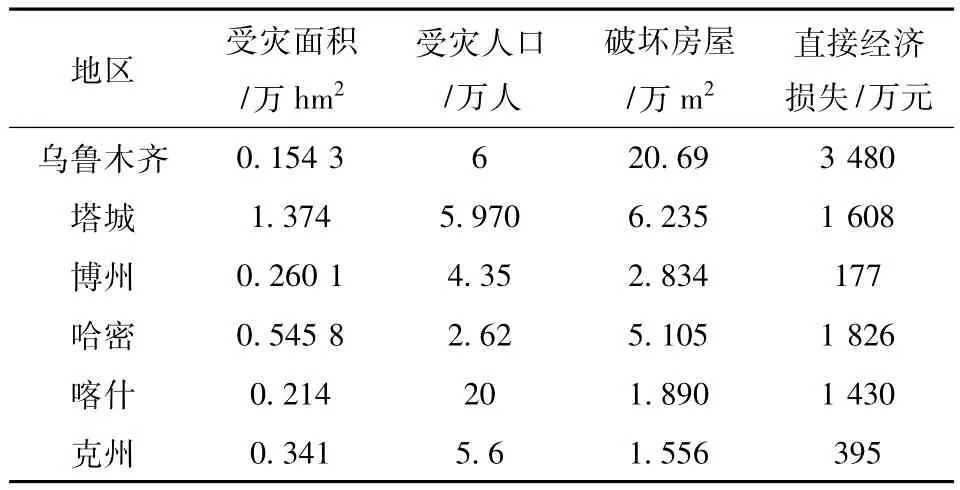
表1 新疆“96.7”洪水损失统计表

表2 自然灾害等级和单指标分级标准

(2)数据处理:自然灾害等级和单指标分级的归一化处理。

先将表2的自然灾害等级和单指标分级标准归一化处理后得到表3，再用表3标准检验模型的合理性后将表1归一化后输入给PCNN模型，采用MATLAB6.5编程计算进而确定新疆“96.7”洪水灾害中6个城市的灾情等级。在表2中各等级取值范围内均匀随机产生各5个样本(表4)，用第2.1节中介绍的步骤对样本逐一分类。该例中β=0.01，θkj为表2中各指标相应等级的范围。

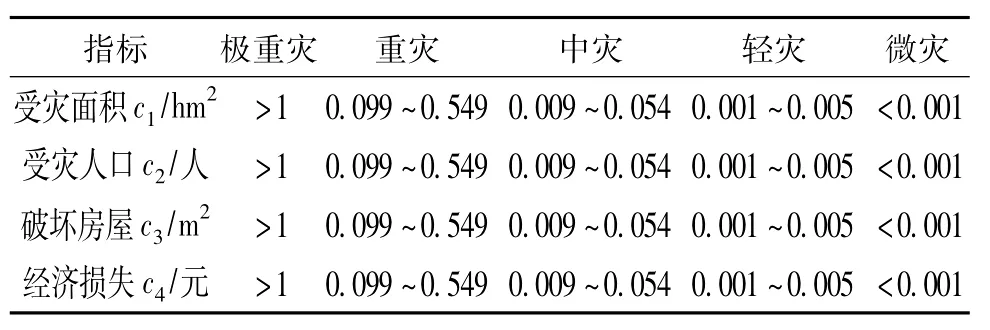
表3 无量纲化后的指标与分类标准

表4 新疆“96.7”洪水灾害灾情分类结果

2.3 评价结果比较

样本值及分类结果见表4。由表4的最后一栏看出PCNN模型对随机产生的25个样本的分类结果理想，故将表1的数据输入给稳定的PCNN模型，得到新疆“96.7”洪水灾害中6个城市的灾情等级，并将此结果与灰色关联法、灰色聚类法、灰色模糊综合3种方法的评价结果进行了比较(表5)。

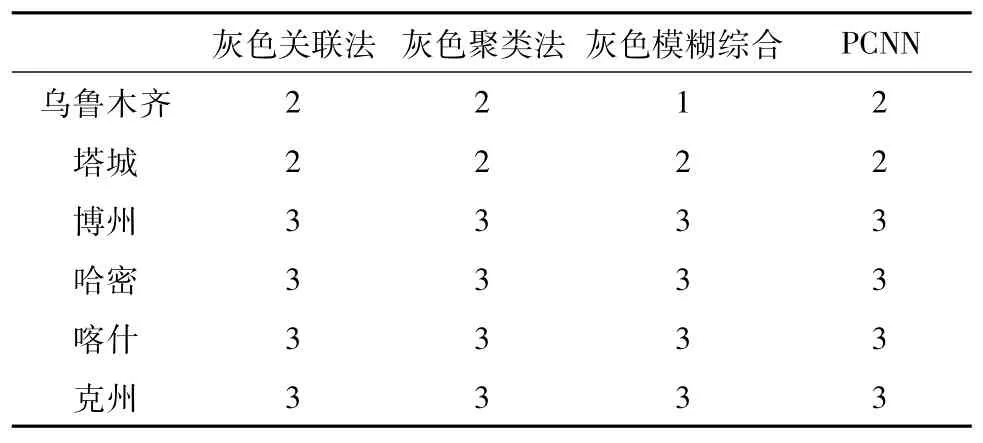
表5 不同评价方法结果比较

对比的结果表明了PCNN在洪水灾害灾情评价中的首次尝试是科学的，能够应用到因洪水灾害造成的破坏程度进行综合评价分类的问题中，对洪水灾害的分类管理具有重要的指导意义［14－17］。

3 结论

(1)PCNN解决了洪水灾情评价这一类评价指标与洪水灾害等级之间复杂的非线性关系的问题，评价结果简便、直观。PCNN把洪水灾情等级取值范围内均匀随机产生的样本以脉冲形式输入，通过脉冲输出从而调节阈值，并且应用动态阈值来确定洪水灾情的等级。评价结果同灰色关联法、灰色聚类法、灰色模糊综合法的评价结果进行了比较，表明其用于洪水损失评价具有科学性和实用性。

(2)PCNN实用性强，文章尝试性在洪水灾害灾情评价问题中应用到PCNN模型。实例表明:PCNN的运行机制、模型结构均比传统的BP模型简单明了;PCNN的运行时间比BP模型短，避免了BP模型中权值的反复训练过程，也没有陷入局部最优从而达不到网络收敛。

(3)PCNN推广性强，脉冲耦合神经网络模型以其更接近生物机制的优越性，被广泛地应用在图像处理、决策优化和通信等方面。本文将PCNN应用于洪水灾情评价是一次新尝试，在PCNN的单个神经元模型结构基础上采用不同反馈输入、连接输入公式和阈值的调整公式，取得了满意的评价结果，证明PCNN应用于灾情评价中是可行的，既拓宽了PCNN的应用领域，又为解决灾情评价问题提供了新的思路。

［1］魏一鸣，金菊良，杨存建，等.洪水灾害风险管理理论［M］.北京:科学出版社，2002.

［2］赵黎明，王康，邱佩华.灾害综合评估研究［J］.系统工程理论与实践，1997，17(3):63－69.

［3］金菊良，魏一鸣，杨晓华.基于遗传算法的洪水灾情评估神经网络模型探讨［J］.灾害学，1998，13(2):6－11.

［4］于庆东.灾度等级判别方法的局限性及其改进［J］.自然灾害学报，1993，2(2):8－10.

［5］赵黎明，王康，邱佩华.灾害综合评估研究［J］.系统工程理论与实践，1997，17(3):63－69.

［6］黄民生，黄呈橙.洪灾风险评价等级模型探索［J］.灾害学，2007，22(1):1－5.

［7］王宝华，付强，谢永刚，等.国内外洪水灾害经济评价评估方法综述［J］.灾害学，2007，22(3):95－99.

［8］刘合香，徐庆娟.区域洪涝灾害风险的模糊综合评价与预测［J］.灾害学，2007，22(4):38－42.

［9］蒋新守，范久波，张继权，等.基本GIS的松花江干流暴雨洪涝灾害风险评估［J］.灾害学，2009，24(3):51－56.

［10］黄蕙，温家洪，司瑞杰，等.自然灾害风险评估国际计划综述Ⅱ－评估方法［J］.灾害学，2008，23(3):96－101.

［11］黄蕙，温家洪，司瑞杰，等.自然灾害风险评估国际计划综述Ⅰ－指标体系［J］.灾害学，2008，23(2):112－116.

［12］李祚泳，邓新民.自然灾害的物元分析灾情评估模型初探［J］.自然灾害学报，1994，3(2):28－33.

［13］黄崇福.自然灾害风险评价理论与实践［M］.北京:科学出版社，2005:111－115.

［14］Gray C M，Singer W.Stimulus－specific neuronal oscillations in the orientation columns of cat visual cortex［J］.Proc，Nat.A-cademy Sci，1989，86(5):1699－1702.

［15］Gu Xiaodong，Yu Daoheng.PCNN's Principles and Applications［J］.Journal of Circuits and Systems，2001，6(3):45－50.

［16］付强.数据处理方法及其农业应用［M］.北京:科学出版社，2006:268－216.

［17］付意成，魏传江，王启猛，等.区域洪灾风险评价体系研究［J］.灾害学，2009，24(3):27－32.