伊犁一矿砾石土三轴渗透试验研究

岳中文，杨仁树,2，孙中辉，窦波洋，韩朋飞

(1.中国矿业大学(北京)力学与建筑工程学院，北京100083；2.深部岩土力学与地下工程国家重点实验室，北京100083)

1 概 述

新疆伊犁地区地下煤炭资源储量丰富，在该地区的大部分地方，第四系表土层中埋藏着一层巨厚砾石层，其中往往含有地下水。在含水复杂多变的砾石层中进行巷道施工，随时面临塌方冒顶、涌水、突水、涌砂和涌泥等一系列问题。因此，要解决富水砾石层井筒支护问题，就必须先了解砾石土的物理力学特性。特别是其渗透性能的影响因素，有必要进行深入的探讨和研究。从国内外的研究状况来看，土中水的研究历史非常悠久，早在1856年法国工程师达西(Darcy)就提出了线性渗流的达西定律[1]。周中等[2]通过自制的常水头渗透仪，测定了不同含砾量时土石混合体渗透系数值。朱崇辉等[3]通过对无黏性粗粒土的颗粒级配，进行控制性渗透试验研究。渗透试验也由饱和土发展到非饱和土，由常规渗透试验进展到三轴渗透试验。但是，三轴渗透性研究仍处在初期阶段，试验技术还很不成熟[4]。能够反映土体三轴渗透研究成果的文献寥寥无几，仅查到朱建华采用应力控制式三轴渗透试验仪研究了土坝心墙的渗透性和渗透各向异性随其所受的应力条件而变化的关系。李永乐等[5-7]利用特制的非饱和土三轴仪，对黄河大堤非饱和土的渗透特性进行了试验研究。如何利用三轴渗透试验对砾石土的渗透规律进行更加系统的研究，以确定更符合实际的砾石土体渗透性参数，便显得尤为重要。

本文利用多功能静动三轴试验机进行渗透试验，研究了伊犁一矿砾石土的渗透特性。通过对伊犁一矿砾石土样进行三轴渗透试验研究，可以有效克服进行常规渗透试验时的先天不足，从而减小误差，为伊犁一矿井筒渗流稳定分析提供更加合理的计算参数。

2 试验描述

2.1 试验仪器

试验采用清华大学水沙科学与水利水电工程国家重点实验室多功能静动三轴试验机，如图1所示。图2表示供水装置，主要有水箱、氮气瓶和压力表组成。

图2 供水装置

该试验机不但能进行土石、软岩与混凝土材料试验，具有轴向与围压独立静动载荷的能力，而且还具有单独渗流以及渗流与应力耦合的各种材料试验功能。加载模式可采用位置控制、应力控制、应变控制及试验过程中的相互转换，可实现计算机全过程控制与数据采集，以及可视化数据处理等。

2.2 试验材料

三轴渗透试验选用不同深度土样三组，试样基本的物理指标见表1。颗粒级配曲线见图3。

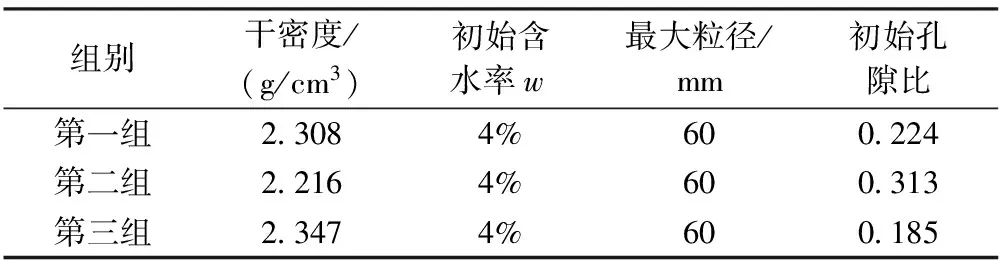
表1 试样的物理指标

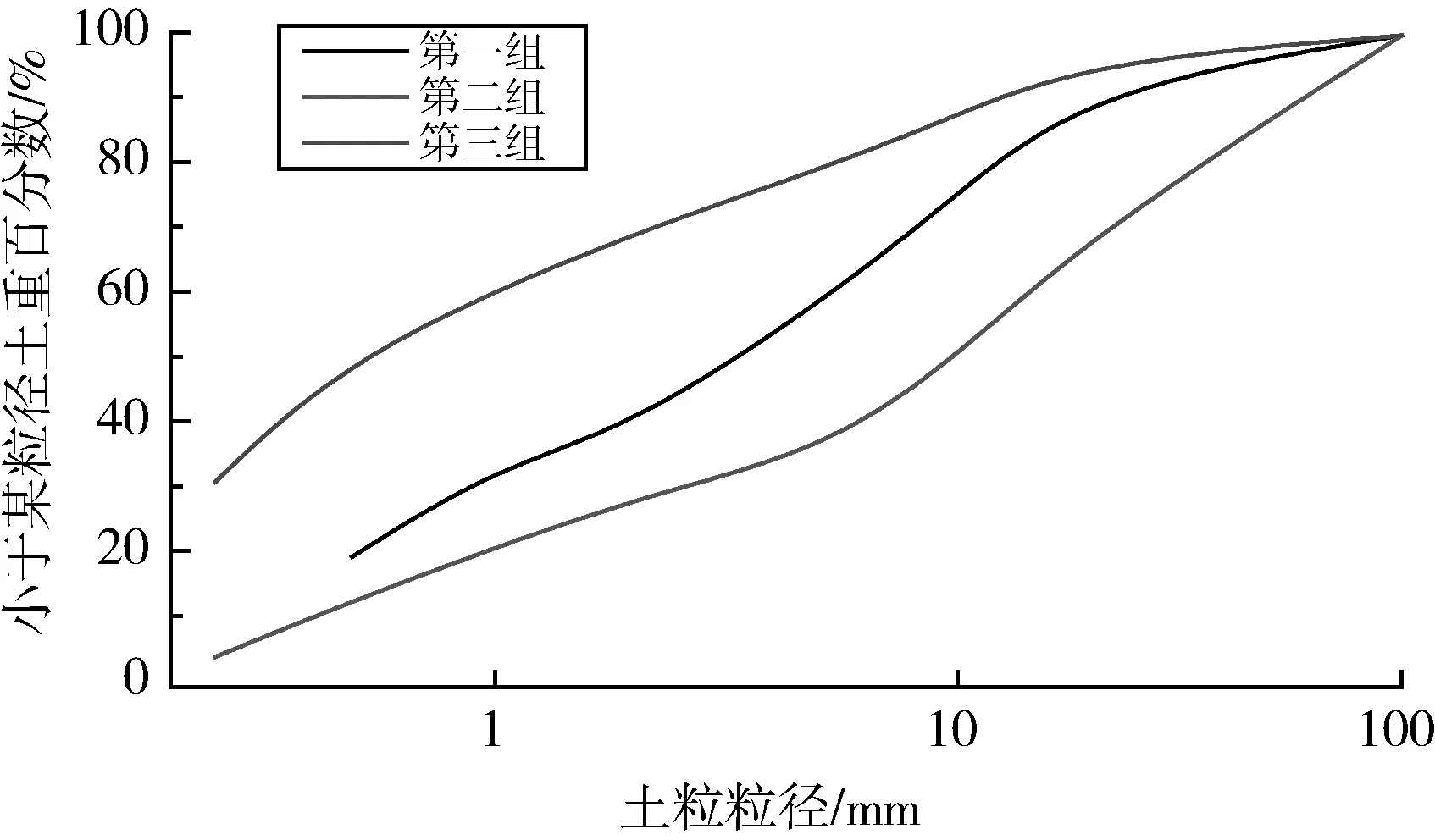
图3 试验材料颗粒级配曲线

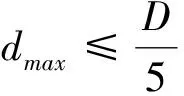
2.3 制样与装样

三轴渗透试验，采用含水率为4%的试样，采用钢制套膜制成垂直样，分四层压实制成。试样尺寸：直径为φ300mm，试样高度为700mm。

2.4 三轴试验原理和加载方案

三轴渗透试验，是通过恒定的周围压力、轴向压力施加至土样，待土样固结完成后，以恒定的流速或恒定的水头对土样进行渗透试验，测量土样在各种条件下的渗透系数。渗透试验分两种试验类型：恒流量试验和恒水头试验。本试验采用恒水头试验。每组围压及水头压力加载方案见表2。

表2 每组围压及水头压力加载方案

2.5 试验步骤

(1)按照三轴试验步骤将试样装好。

(2)施加预定的围压，进行固结排水。

(3)固结完成后，保持围压，用水头压力系统在试样底部施加第一级压力水头，使水从下向上渗透，流量排到体变管中，试样饱和。

(4)经过时间间隔后，记录体变管变化读数，得到在本级压力水头下t时间里的流量Q。记录两次。

(5)调节水头压力系统施加第二级压力水头，重复试验步骤，记录数据。

2.6 计算方法

按每级围压下固结完成后的式样高度H和体积变化量Δq，计算每级围压下固结完成后的试样面积A:

(1)

进行渗透实验，根据Δt时间间隔内的总流量ΔQ，计算单位时间流量q：

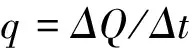
(2)

按试样高度H及压力差ΔP=P1，计算平均水力坡降i：

(3)

将渗流量q、水力坡降i及试样面积A代入下式(4)，计算出在围压σ3作用下的渗流系数k：

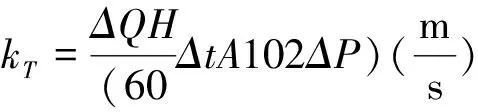
(4)

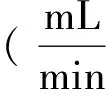
3 试验结果及分析

3.1 初始孔隙比e0对渗透系数的影响

图4表示不同围压条件下的e0-k关系曲线。从图4可见，渗透系数k随着初始孔隙比e0的增大而增大。基本上以围岩σ3=500kPa为界限，大于该围压时，随着孔隙率的增加，渗透系数增加的幅度越来越小；而小于该围压时，渗透系数增加的幅度越来越大，可见围压对砾石土的渗透性影响很大。

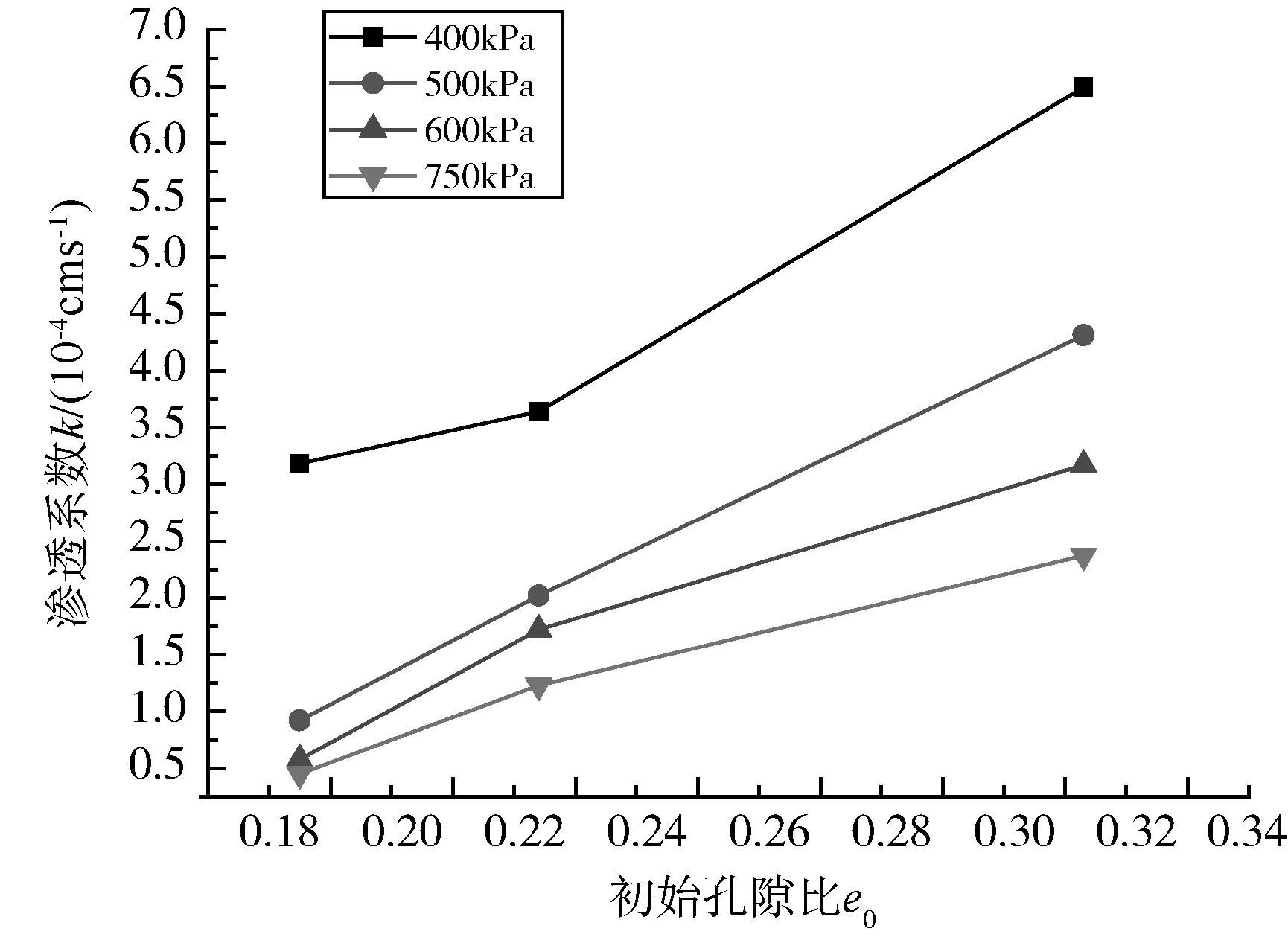
图4 不同围压条件下的e0-k关系图

3.2 不同水头压力对渗透系数的影响

图5、图6和图7分别表示试样在初始孔隙比e0=0.224、e0=0.313和e0=0.185时，在不同的围压条件下，渗透系数随着水头压力变化的关系曲线。由三个图总的变化趋势可以看到，渗透系数是随着水头压力的增大而增大的。同时可以看到，渗透系数和水头压力具有线性的关系。还可以看到，在相同的水头压力下，渗透系数是随着围压的增大而减小的。

图5 e0=0.224时渗透系数-水头压力变化关系

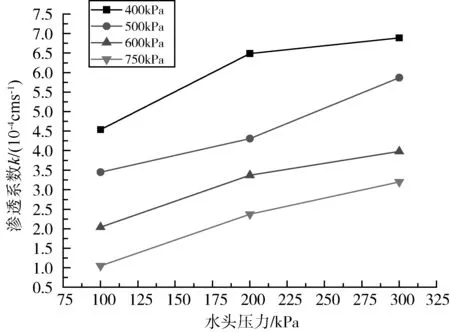
图6 e0=0.313时渗透系数-水头压力变化关系

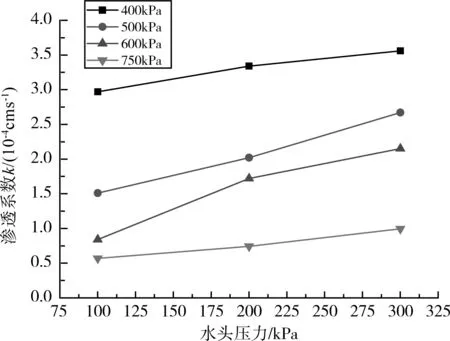
图7 e0=0.185时渗透系数-水头压力变化关系

3.3 围压σ3对渗透系数的影响

图8表示不同初始孔隙比e0条件下的σ3-k关系曲线。从图8可见，渗透系数k随着围压σ3的增大而减小。同时可以看到，随着初始孔隙比e0的减小，渗透系数也在减小。这是因为随着围压σ3的增大，一方面土样固结，有效应力增加(σ′=σ3-P,P为渗水压力)，孔隙比减小，即对骨架的影响较大；另一方面，也增大了水压力，即对渗透水流也会产生一定的影响。

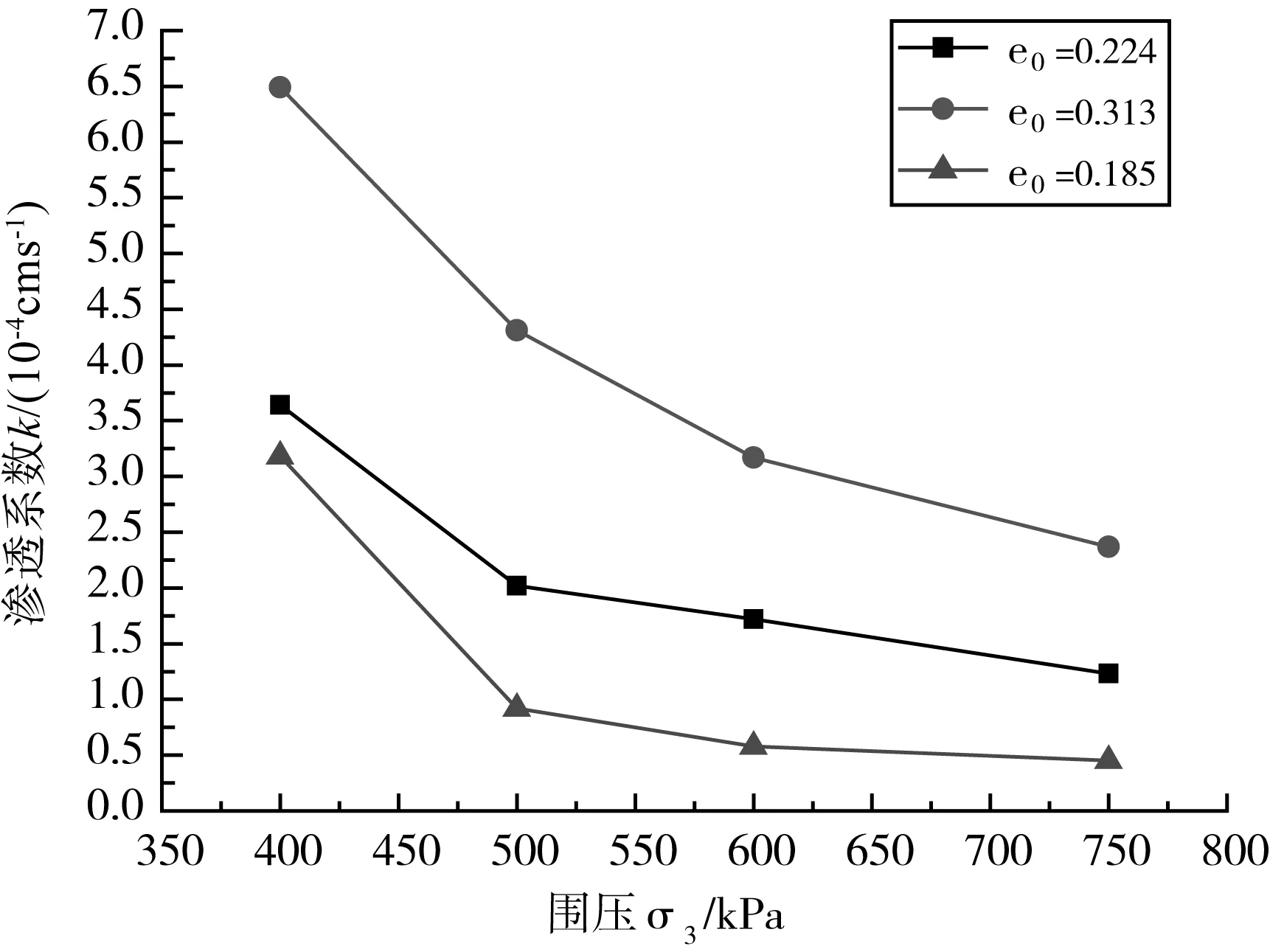
图8 不同初始孔隙比e0条件下的σ3-k关系图

4 结 论

本次研究利用多功能静动三轴试验机室内试验方法，进行不同级配、初始孔隙比和水头压力的砾石土渗透试验研究。研究结论为：①渗透系数k随着初始孔隙比e0的增大而增大；②渗透系数k是随着水头压力的增大而增大的。渗透系数和水头压力具有线性的关系；③在相同的水头压力下，渗透系数k是随着围压的增大而减小的。

[1] 屈智炯. 对粗粒土渗透变形研究的进展[J]. 水电站设计, 2008, 24(1): 48-55.

[2] 周中，傅鹤林，刘宝琛，等. 土石混合体渗透性能的试验研究[J]. 湖南大学学报(自然科学版), 2006, 33(6):25-28.

[3] 朱崇辉, 刘俊民, 王增红. 无黏性粗粒土的渗透试验研究[J]. 人民长江, 2005, 36(11): 53-55.

[4] 刘萌成，刘汉龙，陈远洪，等. 堆石料变形与强度特性的大型三轴试验研究[J]. 岩石力学与工程学报，2003，22(7)：1104-1110.

[5] 李永乐，张红芬，佘小光，等. 原状非饱和黄土的三轴试验研究[J]. 岩土力学, 2008, 29(10): 2859-2863.

[6] 李永乐，刘汉东，刘海宁，等. 黄河大堤非饱和土土水特性试验研究[J]. 岩土力学，2005，26(3)：347-350.

[7] 李永乐，崔翔宇，张红芬，等. 黄河大堤非饱和土的三轴试验研究[J].岩土力学，2006，27(2)：656-660.