基于改进Lorenz系统的多翼混沌吸引子及其电路设计

薛 薇，郭彦岭，沐晶晶

(天津科技大学电子信息与自动化学院，天津 300222)

基于改进Lorenz系统的多翼混沌吸引子及其电路设计

薛 薇，郭彦岭，沐晶晶

(天津科技大学电子信息与自动化学院，天津 300222)

在以 Lorenz系统为基础的一个新混沌系统上添加驱动信号，提出一个新的多翼对称非自治混沌系统.在某一固定频率下，该系统出现了 20翼的混沌吸引子.从仿真结果可以看出，此种改造方法不仅保留了原系统的混沌特性，而且增加了吸引子的拓扑结构复杂性.最后，设计了系统的模拟电路，从物理上验证新系统的混沌特性和数值仿真的一致性.

混沌；吸引子；电路设计；Lorenz系统

Lorenz在1963年发现第一个经典混沌系统——Lorenz系统[1].混沌系统具有丰富的非线性动力学特性，混沌的研究已广泛渗透于数学、科学和工程技术等领域.随着社会的进步、科技的发展，混沌动力学的研究也越来越深入，并且取得了重大发展，国内外许多学者对混沌特性做了大量的分析和研究[2–14].1984年，Chua提出第一个混沌电路，Chua电路为混沌理论的研究提供了一个新的方法，建立了混沌和实际模拟电路的联系[2].1999年 Chen等在 Lorenz系统的基础上利用混沌反控制方法成功构造了一个新的系统——Chen系统[3].2002年 Lü等提出了新的系统——Lü系统[4].2005年Qi等提出了新的4翼自治混沌系统——Qi系统[5–7].

同时，随着混沌研究的逐步深入和越来越多的科研工作加入混沌研究领域，出现了多翼混沌系统.1993年Miranda和Stone提出了一个可以产生n涡卷吸引子的混沌系统[8].2006年Yu等通过n阶多项式参数转换提出了一个基于 Lorenz系统族的多翼混沌吸引子[9]，在 Chua电路的基础上添加非光滑的线性函数如分段函数[10]、阶梯函数[11]及饱和函数[12]等来实现多种广义的 Chua电路.但上述混沌系统模型复杂，用模拟电路实现比较困难.

为了简化系统模型，使其容易用模拟电路实现，文献[13]在 Lorenz系统的基础上构造了一个新的 10翼多吸引子混沌系统.此混沌系统增强了混沌吸引子的拓扑结构复杂性，首次提出了如此多的混沌吸引子，同时系统模型结构简单，容易用电路实现.为了进一步提高系统的动力学特性，在此系统的基础上，本文提出了一种增加混沌多翼特性的方法.在系统中加入某一固定频率的驱动信号，使系统的翼数成倍增长，由 10翼提高到 20翼；实验中驱动信号由信号发生器直接给出，容易操作而且精度高.

1 多翼混沌系统及其混沌分析

文献[13]提出了一种新多翼混沌吸引子的改进Lorenz系统：

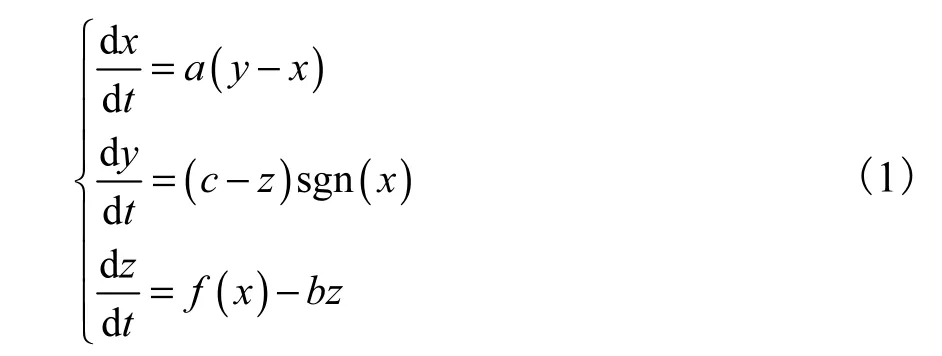
式中：a＝0.9；b＝0.1；c＝2；锯齿波函数 f(x)为

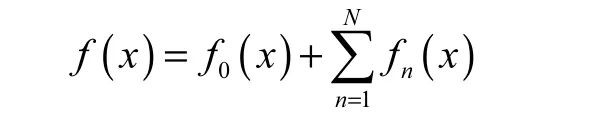
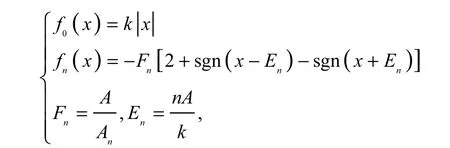
式中：1≤n≤N.当 A＝0.43，k＝2.5，A1＝A2＝A3＝A4＝2.06，F1＝F2＝F3＝F4＝0.208 7，E1＝0.172 0，E2＝0.344 0，E3＝0.516 0，E4＝0.688 0 时，系统(1)可以产生10翼混沌吸引子，如图1(a)所示.

为了能够产生更复杂的混沌吸引子，对系统(1)进行改进，使其关于x–y平面对称.从而产生20翼混沌吸引子，考虑到系统(1)的相图都在 x–y平面的上方，即系统(1)中z不存在负值.因此当令z＝－z时，带入系统(1)，可以得到新系统(2)，系统(2)的参数和其他条件同系统(1)，其混沌吸引子如图 1(b)所示.比较图 1(a)和图 1(b)可以看出，系统(1)和系统(2)是大致关于x–y平面的对称系统.

图1 不同系统的混沌吸引子Fig.1 Chaotic attractors of different system

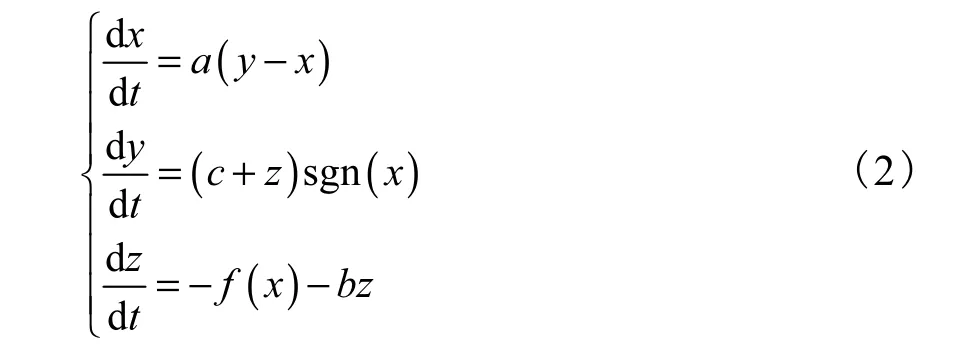
显然，系统(2)和系统(1)有相同的混沌特性.本文对这两种系统外加一驱动信号，使其以固定的频率在这两个系统间切换，可以得到 20翼混沌吸引子的新系统(3).由于每次切换并不改变系统参数，对系统(1)或系统(2)来说，只是改变初始值.因此，系统(3)也是一个混沌系统.

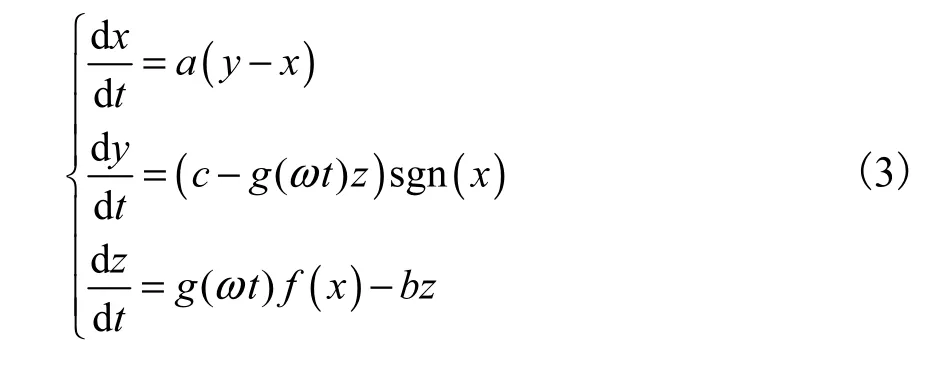
式中：a＝0.3；b＝0.7；c＝2；g(ωt)为方波函数，

系统(3)是以系统(1)为基础，在第二和第三个方程里加上驱动信号 g(ωt).ω为输入方波的角频率，它与频率f的关系为ω＝2πf，输入信号的幅值为1.

系统(3)是一非自治系统，由于时间 t的存在，在分析和计算时远不如自治系统方便，因此将系统(3)等价转换为一个四维自治系统，即

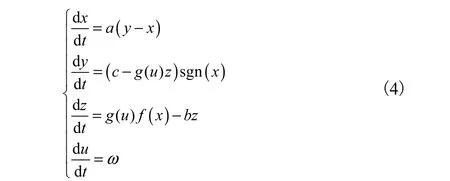
系统(4)的参数和系统(3)相同.当ω＝0.05，A＝0.43，k＝2.5，A1＝A2＝A3＝A4＝2.06，F1＝F2＝F3＝F4＝0.908 7，E1＝0.875 0，E2＝1.750 0，E3＝2.625 0，E4＝3.500 0时，系统(4)的多翼混沌吸引子如图 2(a)所示.

图 2(b)是系统(4)关于参数ω的 Lyapunov指数谱，显然系统(4)是一混沌系统，从图中可以看出ω在[－1，0.1]范围内最大 Lyapunov指数始终是正的，此时系统处于混沌状态，ω在(0.1，1]范围内最大Lyapunov指数为 0，其他指数为负，此时系统处于周期状态.

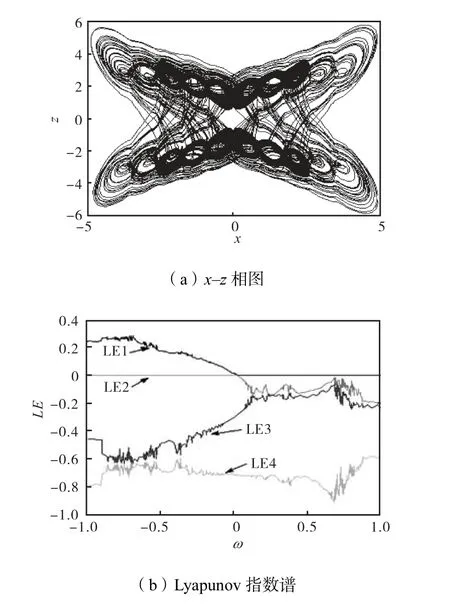
图2 系统(4)的x-z 相图和Lyapunov指数谱Fig.2 Phase portrait of system (4) on the x-z plane and its Lyapunov exponents

2 模拟电路设计和multism电路仿真

混沌系统最直接和简单的物理实现是通过电路完成的[12].基于此目的对系统(3)进行 multism 电路仿真.首先，为了能够搭建电路模型要对系统进行转换，将系统(3)的微分电路模型转换为积分电路模型(5).考虑到电路主要靠运算放大器来实现，运算放大器本身的比例环节有一个负号，积分电路本身也有一个负号，应对系统(5)进行变换.同时，由于示波器本身有一个扫描频率，为了让示波器能够显示混沌信号，需要对电路信号的频率进行调整：

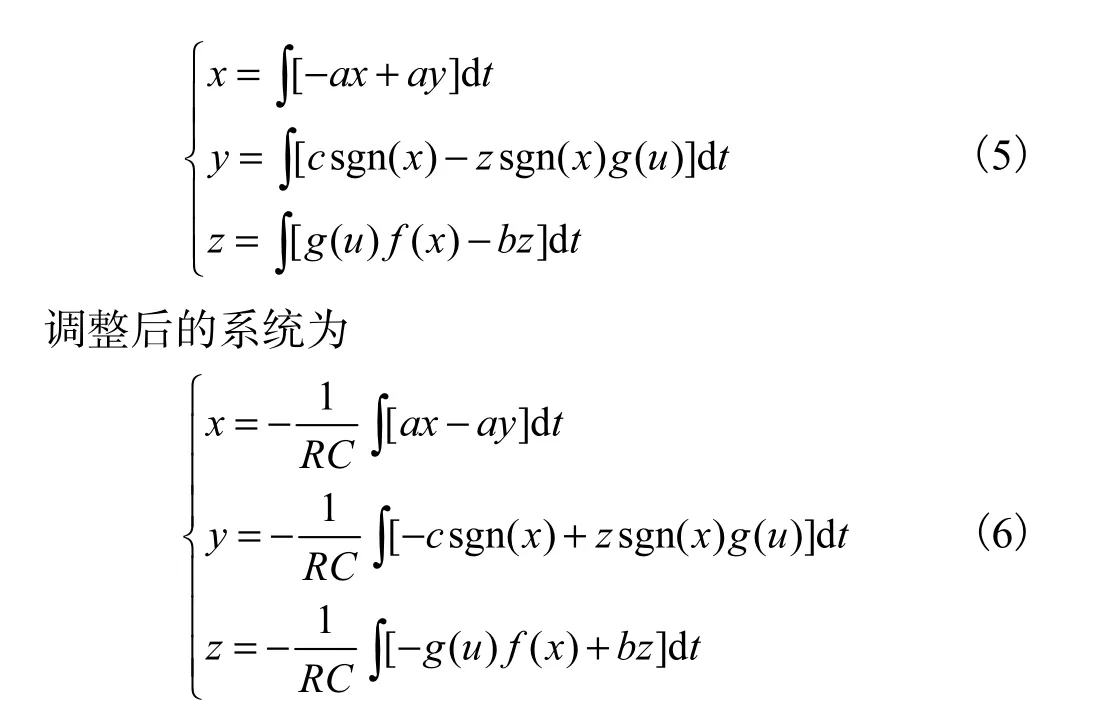
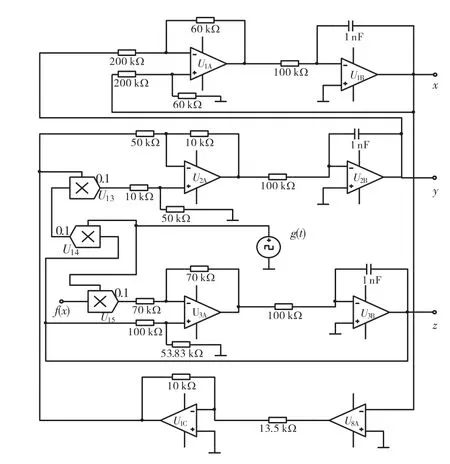
图3 系统(6)的电路实现Fig.3 Circuit implementation of system(6)

考虑到实际模拟乘法器 AD633的输出有一个0.1倍的缩小，因此对输入信号进行了 10倍的放大，取方波信号的输出为10,V，得到的multism仿真结果如图5所示.

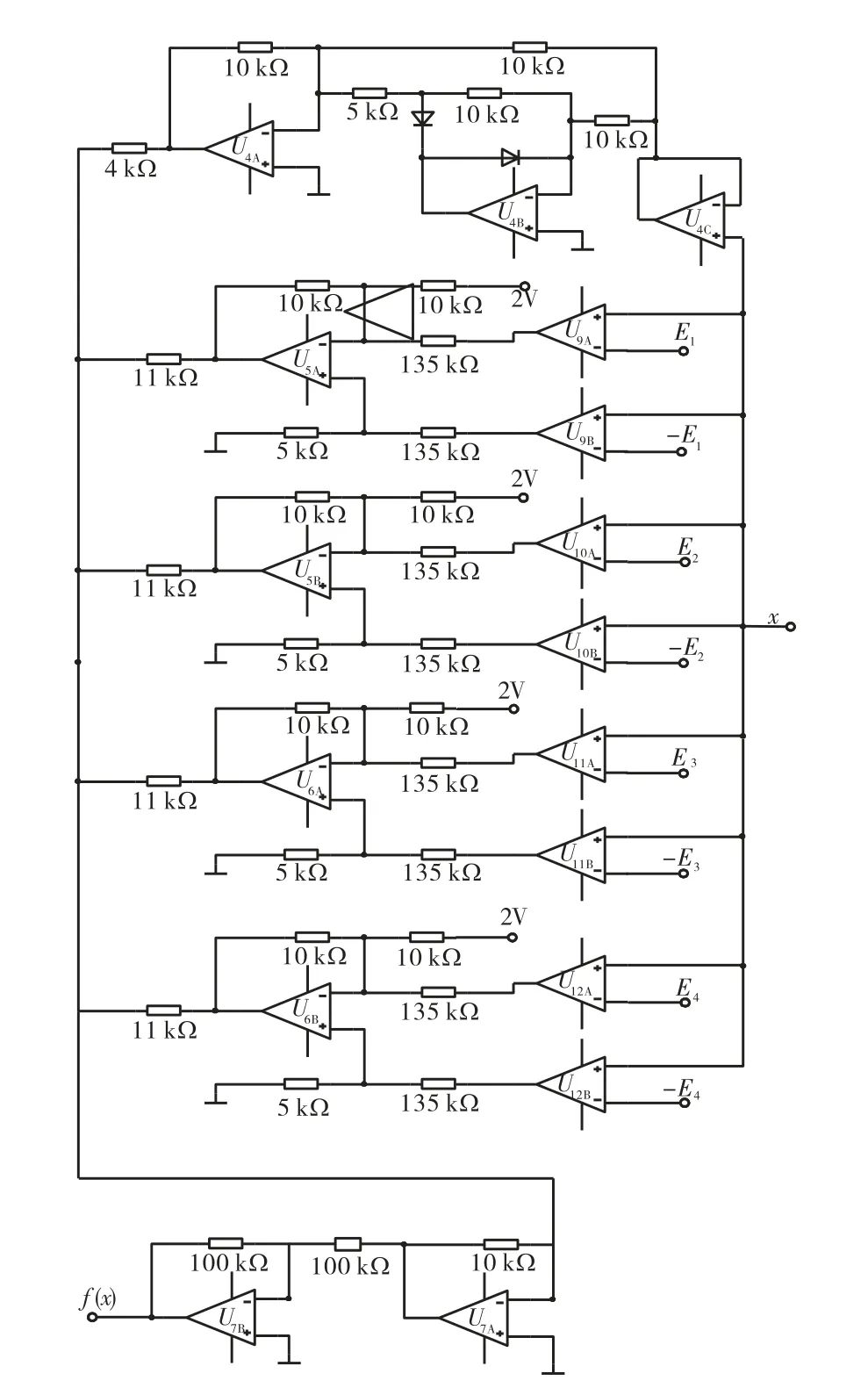
图4 非线性函数f(x)的电路实现Fig.4 Circuit implementation of nonlinear function f(x)

图5 系统(6)的multism电路仿真结果Fig.5 Multism circuit simulation of system(6)

比较图 2(a)和图 5可以看出电路结果和数值仿真结果基本一致.从物理层面证实了此系统的混沌吸引子的存在性和其吸引子拓扑结构的复杂性.同时，此系统的实现电路简单，更易于应用实际，特别是应用于通信加密系统.

3 结 语

本文通过对文献[13]提出的一种基于 Lorenz系统的多翼混沌吸引子的分析和改进，得出更加复杂的多翼混沌吸引子.分析表明，改进后的系统不仅保存了原系统的混沌特性，并且增加了吸引子的个数，使得改进后的系统的拓扑结构更具有复杂性.同时，改进后的多翼混沌吸引子系统容易通过模拟电路进行实现，为保密通信和利用混沌加密的领域提供了一种更好的混沌信号发生器的选择方案，增加了信号的安全度，使其更难破译.

［1］Lorenz E N. Deterministic non-periodic flow[J]. Journal of Atmosphere Science，1963，20：130–141.

［2］Matsumoto T. Chaotic attractor from Chua's circuit[J].IEEE Transactions on Circuits and Systems，1984，CAS-31(12)：1055–1058.

［3］Chen G R，Ueta T. Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos，1999，9(7)：1465–1466.

［4］Lü J H，Chen G R. A new chaotic attractor coined[J].International Journal of Bifurcation and Chaos in Applied Sciences and Engineering，2002，12(3)：659–661.

［5］Qi G Y，Du S Z，Chen G R，et al. On a four-dimensional chaotic system[J]. Chaos，Solitons & Fractals，2005，23(5)：1671–1682.

［6］Qi G Y，Chen G R，Zhang Y. Analysis and circuit implementation of a new 4-D chaotic system[J]. Physics Letters A，2006，352：386–397.

［7］Qi G Y，Chen G R，Li S，et al. Four-wing attractors：from pseudo to real[J]. International Journal of Bifurcation and Chaos，2006，16：859–885.

［8］Miranda R，Stone E. The proto-Lorenz system[J].Physics Letters A，1993，178(1/2)：105–113.

［9］Yu S M，Lu J H，Tang W K S，et al. A general multiscroll Lorenz system family and its realization via digital signal processors[J]. Chaos，2006，16(3)：033126.

［10］Chua L O，Roska T. The CNN paradigm[J]. IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，1993，40(3)：147–156.

［11］Yalcin M E，Suykens J A K，Vandewalle J，et al. Families of scroll grid attractors[J]. International Journal of Bifurcation and Chaos，2002，12(1)：23–41

［12］Lü J H，Chen G R，Yu X H，et al. Design and analysis of multi-scroll chaotic attractors from saturated function series[J]. IEEE transactions on circuits and systems I，2004，51(12)：2476–2490.

［13］Yu S M，Tang W K S，Lü J H，et al. Multi-wing butterfly attractors from the modified Lorenz systems[C]//Proceedings of IEEE International Symposium on Circuits and Systems，Piscataway：IEEE，2008：768–771.

［14］仓诗建，陈增强，袁著祉. 一个新四维非自治超混沌系统的分析与电路实现[J]. 物理学报，2008，57(3)：1493–1501.

A Multi-Wing Chaotic Attractors of the Modified Lorenz System and Its Circuit Design

XUE Wei，GUO Yan-ling，MU Jing-jing
(College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China)

A novel non-autonomous chaotic system with multi-wing and symmetry was proposed by adding a driving signal to a chaotic system based on Lorenz system. The system may have twenty-wing chaotic attractors at a fixed frequencyof the input signal. Simulation results show that the chaotic property is preserved in the novel system，and moreover，the complexity of topological structure of attractors is enhanced. Finally，an analog electronic circuit was designed to implement the novel system physically. Experimental results of the novel chaotic circuit well agree with the simulation results.

chaos；attractor；circuit design；Lorenz system

TM132； O415.5

A

1672-6510(2010)05-0045-04

2010-06-02；

2010-07-12

国家自然科学基金资助项目（10772135；60784028）

薛 薇（1963—），女，河北河涧人，副教授，xuewei@tust.edu.cn.