火灾与气象因素的相关性研究
●刘 宁,祝国苓
(天津市消防总队,天津 300090)
0 引言
火灾预测是火灾系统领域中一个不可缺少的课题,对一个具体火灾而言是随机和偶然的,但对于一个城市或地区的火灾总体,其火灾发生具有一定的规律性。探索整个火灾系统随时间的演变规律,将揭示城市火灾的宏观规律,促进城市火灾的“可持续防治”。
前人通过从已有的研究对城市火灾系统进行了初步的分析,发现城市火灾分布具有明显的幂律分布,而且城市火灾的“频率 -损失”幂律分布具有尺度不变性(即体系经过尺度变换后,其某一特性不变)和时间不变性(即时间靠后的数据不对时间靠前的结果产生影响)。城市火灾的幂律分布表明不同规模,不同时期的火灾具有相互关联,可以由火灾的历史数据预测未来的火灾发生情况,火灾规律的随机性可以用统计的方法进行研究,通过总结、整理和分析大量的火灾原始资料,归纳出火灾发生的随机性规律[1]。
影响城市火灾发生的外界因素很多,除社会经济因素[2]、技术因素、政治因素等,还有自然气象方面的因素。目前对气象因素与火灾之间的关系相对研究较少,但火灾作为一个开放系统,必然在很大程度上受到自然现象的影响,其中气象因素对火灾的发生、防治和损失控制方面有着重要的影响[3-4]。本文以天津市的火灾数据与气象因素进行相关性分析和研究,借助回归理论建立火灾起数与关键气象因素之间的关联模型,并采用已有数据对模型进行了验证,用来说明火灾发生与气象因素的关系。
1 多元线性回归模型[4]
1.1 多元线性回归模型的基本原理与参数估计
许多经济等现象往往受多个因素的影响,研究被解释变量受多个解释变量的影响,可利用多元回归模型。多元线性回归模型假定被解释变量 Y与多个解释变量 X1,X2,…,Xk之间具有线性关系,是解释变量的多元线性函数,称为多元线性回归模型。即
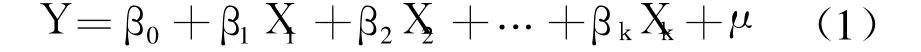
其中,Y为被解释变量,Xj(j=1,2,…,k)为 k个解释变量,βj(j=0,1,2,…,k)为 k+1个未知参数,μ为随机误差项。
被解释变量 Y的期望值与解释变量 X1,X2,…,Xk的线性方程为:

该方程称为多元总体线性回归方程,简称总体回归方程。
与一元线性回归分析一样,多元线性回归分析仍是根据观测样本估计模型中的各个参数,对估计参数及回归方程进行统计检验,从而利用回归模型进行预测和分析。多元线性回归模型包含多个解释变量,多个解释变量同时对被解释变量发生作用,若要考察其中一个解释变量对 Y的影响就必须假设其它解释变量保持不变来进行分析。因此多元线性回归模型中的回归系数为偏回归系数,即反映了当模型中的其它变量不变时,其中一个解释变量对因变量 Y均值的影响。
多元线性回归模型利用普通最小二乘法(OLS)对参数进行估计时,有如下假定:(1)零均值假定:E(μi)=0,i=1,2,…,n;(2)同方差假定(μ的方差为同一常数),;(3)无自相关性:;(4)随机误差项 μ与解释变量 X不相关(这个假定自动成立)随机误差项 μ服从均值为零,方差为σ2的正态分布;(6)解释变量之间不存在多重共线性:rank(X)=k+1≤n,即各解释变量的样本观测值之间线性无关,解释变量的样本观测值矩阵 X的秩为参数个数 k+1,从而保证参数β0,β1,β2,…,βk的估计值惟一。
对于含有 k个解释变量的多元线性回归模型 Y=Xβ+μ,参数 β的最小二乘估计为:
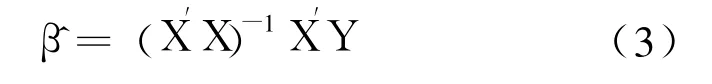
1.2 显著性检验
建立的回归方程需进行实际意义检验和统计检验。实际意义检验主要检验模型参数估计量在实际意义上的合理性。其表现为检验求得的参数估计值的符号与大小是否合理,是否与根据人们的经验和实际理论所拟定的期望值相符合。所有参数估计值通过实际意义检验后,再进行统计检验,统计检验主要包括拟合优度检验(R2检验)、方程显著性检验(F检验)、变量显著性检验(t检验)等。
1.3 利用多元线性回归方程进行预测
要进行预测,可将样本值代入回归方程:

对于给定置信水平 1-α,预测值 Y0置信区间为:

2 火灾发生次数与气象因素的相关性分析
天津市地处华北平原东北部,环渤海湾的中心,东临渤海,北依燕山,处于国际时区的东八区,位于中纬度欧亚大陆东岸,主要受季风环流的支配,是东亚季风盛行的地区,属大陆性气候。主要气候特征为:四季分明,春季多风,干旱少雨;夏季炎热,雨水集中;秋季气爽,冷暖适中;冬季寒冷,干燥少雪。天津年平均气温在 11.4~12.9℃,市区年平均气温最高为 12.9℃。1月最冷,平均气温在 -3~-5℃;7月最热,平均气温在 26~27℃。在四季中,冬季最长,有 156~167天;夏季次之,有 87~103天;春季56~61天;秋季最短,仅为 50~56天。天津年平均降水量为 520~660mm,降水日数为 63~70天。在地区分布上,山地多于平原,沿海多于内地。在季节分布上,6、7、8三个月降水量占全年的 75%左右。
2.1 多元回归模型的建立
本文选取天津市 1997年 ~2007年 11年间的月度火灾发生次数与月平均温度、月平均相对湿度、月平均风速、月平均降雨量等气象因素进行相关性分析。选取月平均温度、月平均相对湿度、月平均风速、月平均降雨量作为影响火灾发生次数的四个气象因素,建立月火灾次数的线性回归模型。本文采用 SPSS软件,通过逐步回归法进行变量筛选并建立线性回归方程。
2.1.1 数据说明
由于 1997年实施了新的火灾统计方法,将以往难以统计的小火灾计入火灾发生数中,影响了火灾数据的连续性,火灾发生数在 1997年前后不具有可比性。由于找不出合适的数学手段来调整这种数据的跃变,笔者仅对 1997年及其以后的数据进行处理。其中,1997~2003年天津市火灾起数来自《中国火灾统计年鉴》(1997-2003),数据如图 1所示,2004~2006年天津市火灾起数来自《中国消防年鉴》(2004-2006),按照当时的统计标准,火灾起数即消防队出火警次数,到了 2007年,统计标准改变,仅将造成损失的火警数统计为火灾数据,为保持数据统计标准的连贯性,笔者选择由天津市消防局记录的月出火警次数作为 2007年的火灾起数。[5-6]
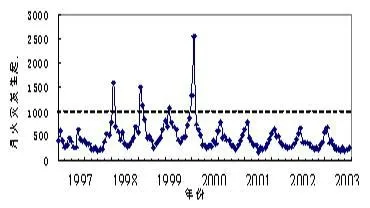
图1 天津市 1997~2007年间月火灾发生起数
2.1.2 异常值处理
从图 1可以看出,天津市 1997~2007年间的月火灾发生起数以年为单位呈现大致的周期性变化。本文将该参数作为被解释变量 Y,出于统计意义的考虑,在建立多元线形回归模型之前,先要对数据进行异常值剔除。笔者删除了火灾发生次数大于1 000的 6个数据,即图 1中虚线以上的点,剩余 126个数据作为后面建立回归模型的依据。
2.1.3 线性相关分析
利用进行异常值处理之后的样本数据计算火灾发生次数 Y与月平均温度 X1、月平均相对湿度 X2、月平均风速 X3、月平均降雨量 X4之间的相关系数,见表 1所示。

表1 线性相关系数表(1997-2007)
从表 1中,可以看出气象因子对月火灾发生起数的影响从大到小依次为:X1、X4、X2、X3,月平均温度 X1是最主要的影响因素,相对湿度和降雨量是次于温度影响的气象因子,月平均风速对火灾发生的影响相对较小。火灾发生起数与月平均温度的相关系数为负,说明二者是负相关的,即平均温度越低越容易发生火灾,平均温度越高越不容易发生火灾,这是因为环境气温直接影响引燃物品的含水量;而降雨量直接影响空气湿度的变化,从而影响引燃物的含水量。风速对城市火灾发生的直接影响不大,但必须注意,风速对火灾的蔓延影响较大,当风速达到一定值时,容易产生飞火,导致第二火场。
2.1.4 根据逐步回归方法,得到进入回归方程的自变量为月平均温度和月平均降水量,并得到回归方程中的系数如表 2。
根据表 2,采用非标准化系数,可以建立如下回归方程:

表2 回归方程系数表
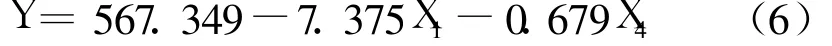
判定系数 R2=0.543,在显著性水平 α=0.05下,检验统计量F=30.108>F0.95(2,127)=2.35,(p-值 0.000<0.05)即线性回归方程是显著的。
在 0.05置信水平下,变量 X1,X4均能通过 t检验,因为常数项、变量 X1、X2的检验 p-值分别为0.000、0.000、0.002,都小于 0.05,所以我们建立多元线形回归模型式(6)是合适的。
为进一步考察回归方程的合理性,采用 2008年1~7月份的气象数据对方程进行验证,原始气象数据如表 3。将原始气象数据代入式(6),可得到月火灾起数的预测值与实际值的对比如图 2所示。
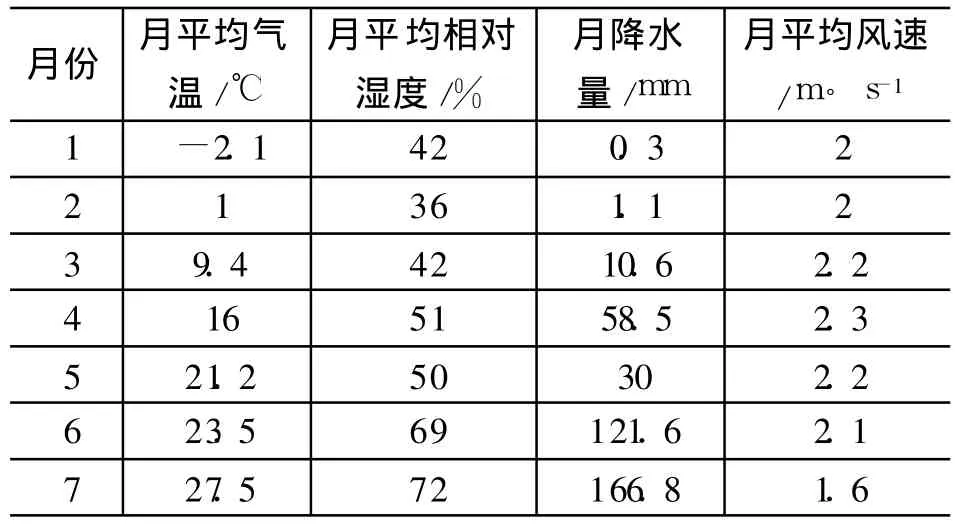
表3 2008年 1~7月份气象数据
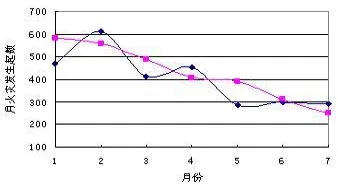
图2 2008年 1~7月份月火灾发生起数对比
从图 2中可以看出,回归模型较好地预测了 2~7月份的火灾发生趋势,这 6个月火灾发生起数总体呈下降趋势,这与统计数据是一致的。但其中 1、3和 5月份的预测值比实际值高,以 1月份差别最大,首先是因为火灾的发生受多重因素影响,气象并非影响火灾发生的惟一原因,故仅采用气象因素预测火灾发生起数本身有一定的局限性;其次是 1月份我国许多地区发生雪灾,天津也未能幸免,大量降雪导致室外空间在很长一段时期内被雪覆盖,室外的可燃物很难起火,所以实际值和预测值的差别较大。
2.2 多元回归模型的应用
多元回归模型对预测城市火灾的发生趋势具有较好的参考意义,要预测未来年份的月火灾发生起数,必须先获得未来年份的气象数据。图 3是天津市 1997~2007年的月平均气温,数据以年为单位呈现极为规则的周期性,气温最低的月份一般为 1月,最高的月份为 7月。图4是天津市 1997~2007年的月平均降雨量,也呈现较为明显的规律性,每年冬季降雨量较低,夏季降雨量较高。我们在对未来年份的火灾发生趋势进行预测分析时,可以对之前若干年份的月平均气温和月平均降雨量取平均值,作为解释变量代入式(6)中,得到预测结果。
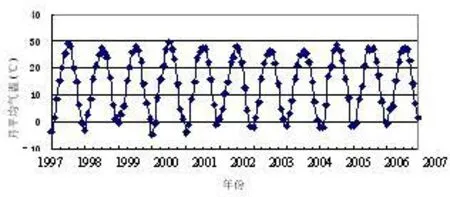
图3 天津市 1997~2007年的月平均气温

图4 天津市 1997-2007年的月平均降雨量(mm)
3 结论
气象因素在许多火灾过程中并不一定是引起火灾发生的直接原因,但与火灾发生和发展有着密不可分的相互关系。基于对城市火灾和气象因素的相关性分析,建立必要的监测理论模型及实施系统,对城市火灾进行早期预防,以减少城市火灾的危害,具有相当程度的实际价值。本文针对天津市的火灾数据与气象因素进行相关性分析和研究,借助回归理论建立火灾起数与关键气象因素之间的关联模型。结果表明,天津市全年火灾发生的高发期出现在 1、2、3、12月冬春之际,气温低、用火用电明显增多,相对湿度小,可燃物含水量低,极易引发火灾。且逢元旦、春节,人们节前生活繁忙、节中精神松懈,往往忽略火源管理,加上节日期间普遍燃放烟花爆竹,造成火灾高发,因此在这几个月中,政府消防工作的重点应当在节假日前后的消防安全宣传、对重点防火的部位如公众聚集场所的预防火灾治理和灭火救援工作上。
[1]宋卫国,王健.火灾系统的复杂性与可持续防治[J].科技导报,2004,25(8):17-20.
[2]杨立中,江大白.中国火灾与社会经济因素的关系[J].中国工程科学,2003,5(2):62-67.
[3]康嫦娥.城市火灾的气象条件分析及火险预报[J].气象,1993,19(7):47-51.
[4]馀耀标,许平.城市火灾浅析[M].北京:气象出版社,1992:14-85.
[5]公安部消防局.中国火灾统计年鉴(1997-2003)[M].北京:中国人民公安大学出版社.
[6]公安部消防局.中国消防年鉴(2004-2006)[M].北京:中国人事出版社.

