运动员技能诊断与规划的灰色理论与方法研究——以高水平田径运动员专项技能培养为例
孙桂云,王雁玲,刘嘉津,杨森
(宁波大学,浙江 宁波 315211)
目前灰色理论方法在体育领域的应用主要集中在竞技体育领域,但多为某些独立问题的个别研究。从研究整体状况看,研究缺乏深度,理论不够系统。因而大大降低了灰色理论方法在体育领域的应用效率,使原本最适合竞技体育动态分析和个体化研究的独特性质没有得到充分发挥。这里所做的研究就是将灰色理论与田径专项技能训练紧密结合起来,运用灰色方法实现田径专项技能系统的优化,使田径训练更具科学性和可控性。
1 研究对象与方法
1.1 研究对象
高水平田径运动员个体专项技能培养过程中,实施动态量化模型调控的灰色理论与操作方法。
1.2 研究方法
灰色关联分析、GM(1,1)模型、GM(1,1)残差模型、GM(2,1)模型、GM(1,2)模型以及灰色系统预测模型方法。
2 结果与分析
2.1 优化方法的整体构造
对于田径运动员专项技能的系统优化,我们可以从以下几个方面逐步展开。首先,要了解运动员专项技能可能达到的理想水平,或希望达到的理想水平,即:专项技能发展趋势预测。这一工作主要目的是大体把握运动员发展潜能和近期目标。然后,对运动员专项技能所涉及的相关指标进行筛选,找出与运动员专项技能密切相关的重点指标,为建立运动员专项技能系统模型做准备。接下来,要对运动员建立包含运动员专项技能重点相关指标的多因素灰色模型,即:建立运动员专项技能及其相关因素指标的模型控制系统。最终,采用指标模型与多因素整体模型相结合的方式,逐一对运动员专项技能指标进行预测,以此对运动员专项技能训练进行具体的量化指标定位。
2.2 系统优化控制的具体方法
2.2.1 专项技能发展趋势的预测专项技能发展趋势可分为两种,一是从运动员自身发展趋势出发,预测未来可能的发展潜能;二是从运动员培养任务出发,预测当今运动员所处的环境,以未来整体发展趋势水平为参照,为运动员设定近期发展目标。由于体育事件包括田径运动专项技能的发展存在着较强的阶段性特征,如运动员运动水平有“起萌”、“上升”、“维持”、“下滑”之分;运动项目的发展可以有“初创”、“发展”、“成熟”,有时还会出现“低谷”等。从预测角度上讲,采用不同发展阶段的数据,对体育事件的发展趋势做出预测必然会存在巨大的差异,因而了解体育事件目前所处的发展阶段对预测的准确与否至关重要。解决这一问题,从简便操作方法出发,主要可以采用GM(1,1)模型、GM(1,1)残差模型和GM(2,1)模型3种方法实现。最基本的方法是GM(1,1)模型方法,但当原始数值摆动偏大时,可以采用GM(1,1)残差模型加以修正,而当存在明显转折事件出现时,则采用GM(2,1)模型方法。我们采集了第14~28届奥运会女子铅球的冠军成绩,对其中第14~27届成绩进行分段建模比较分析,并保证所有模型预测值都有实际成绩进行验证。分段的方法是选择“转折期”、“转折前期”和“转折后期”三段进行 GM(1,1)与GM(2,1)建模对比,具体情况见图1。
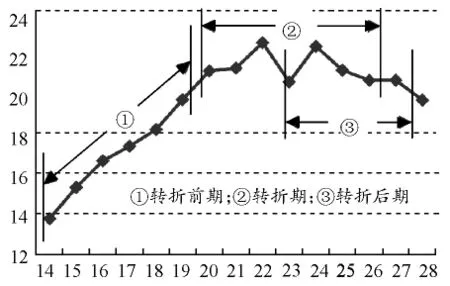
图1 第14~28届奥运女子铅球冠军成绩及分段建模示图
经计算,得到各段模型见表1。
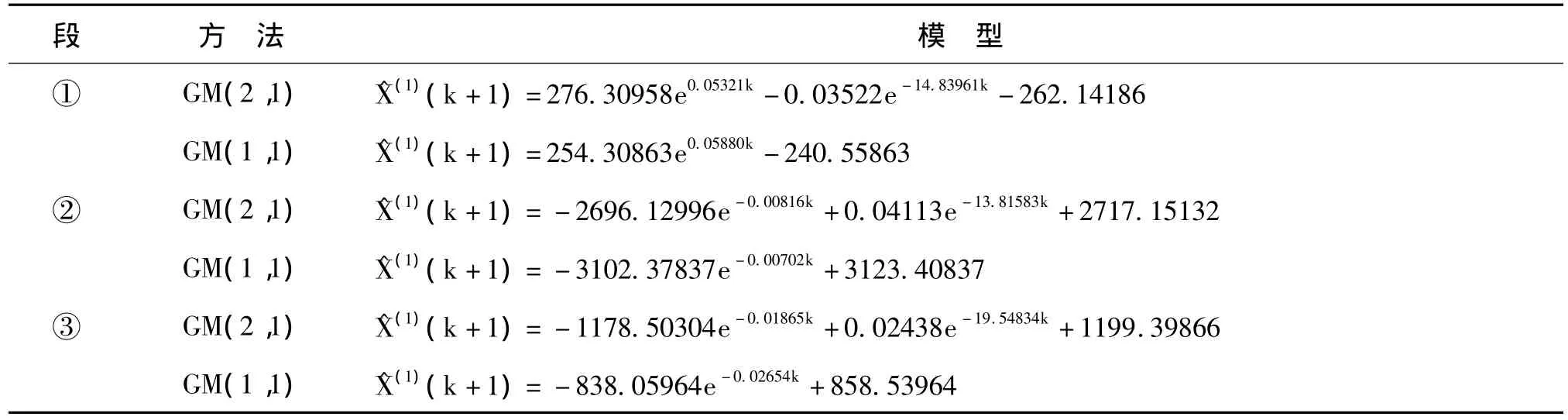
表1 “转折前期”、“转折期”和“转折后期”的GM(2,1)与GM(1,1)模型
对以上模型进行检验和与实际值对比分析表明(见表2):
在对相对平滑的数据列进行建模预测时(即:转折前期),两种模型都为一级,但GM(1,1)模型精度更高(C=0.0912明显小于GM(2,1)的 C=0.1247),误差对比也表明,GM(1,1)预测值的误差为1.76%,而GM(2,1)预测值的误差要大出3.59倍。因而此时应采用GM(1,1)方法建模预测。
在对具有轻微摆动数据列进行建模预测时(即:转折后期),一般情况下,GM(2,1)建模方法不亚于GM(1,1)建模方法。具体问题应视摆动幅度而定,幅度越大越适合采用GM(2,1)方法。
在对有明显的摆动数据列进行建模预测时(即:转折期),GM(1,1)模型的检验精度为四级,已无法作为正常的预测模型,只能用GM(2,1)来解决建模问题。此处误差对比也看出,GM(2,1)的预测结果还是十分理想的。
另外,多年预测实践经验提示我们,如果原始数据量较大,采用GM(1,1)还是 GM(2,1)建模预测,可能还不仅仅要考虑数据摆动幅度的大小问题,与转折期所处的位置也可能有关。一般说,转折期处在被预测原始数据的前段,往往用GM(1,1)模型可以预测;如果处在被预测原始数据的中段,将不能预测或只能用GM(2,1)模型预测;如果处在被预测原始数据的后段,则多采用GM(1,1)残差模型预测。
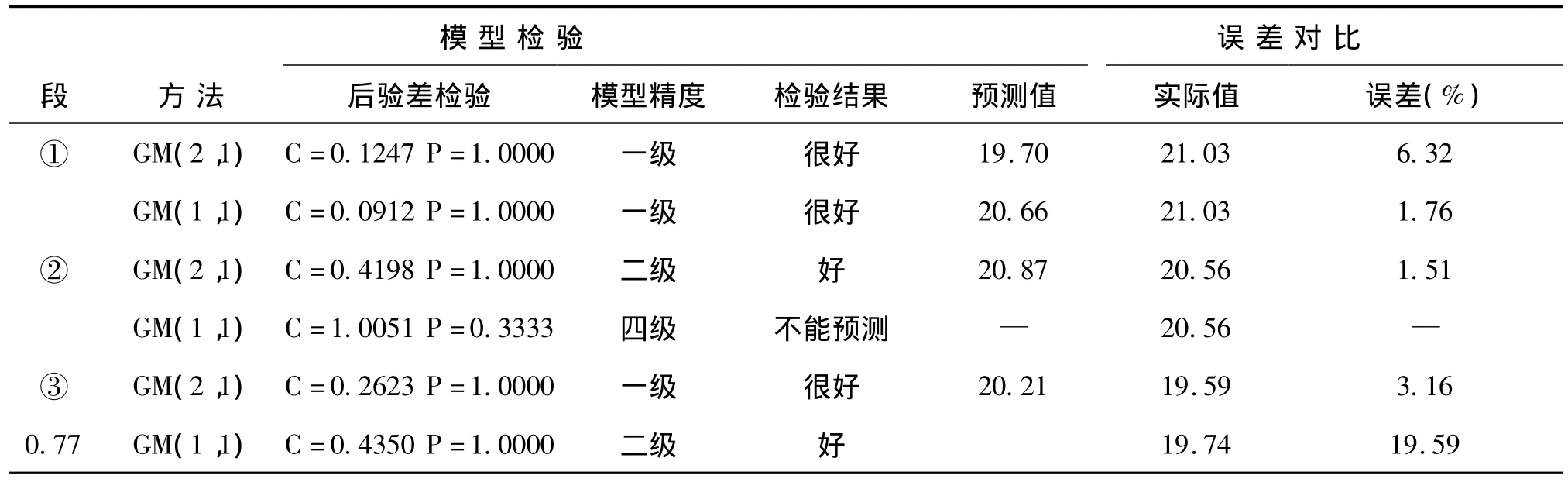
表2 GM(2,1)与GM(1,1)在不同分段情况下的模型精度比较
2.2.2 专项技能重点指标的筛选运动员的专项技能特征主要体现在运动员的各项运动指标上,选择出合适的运动指标,对运动员进行有针对性的训练,是当今运动训练领域实施科学训练的关键。
运用灰色关联方法对田径运动员专项运动技能指标进行筛选的最大优势,就是可以运用运动员技能指标的连续性特征来弥补运动员个体分析数据量少的缺陷,使我们的分析完全适合于运动员的个体特性,而不是众多运动员的共同特征。
灰色关联分析的具体方法:[2](1)建立指标特征值矩阵。(2)对指标进行无量纲化处理。(3)确立指标权重。(4)进行灰色关联度计算。
以女子链球运动员顾原为例(表3),运动灰色关联分析方法,筛选其专项技能的重要相关因素指标。
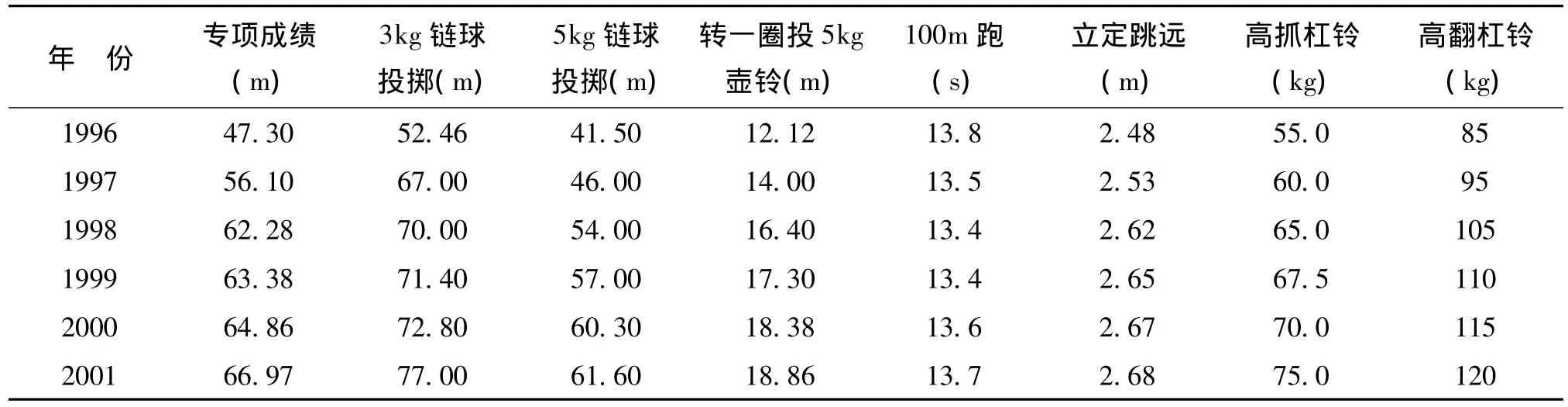
表3 顾原的专项成绩与各素质指标关系一览表[4,5]
由表4我们可以看出顾原专项能力最重要的素质指标为:3kg链球投掷、5kg链球投掷和高翻杠铃。

表4 顾原专项成绩与各素质指标间的灰色关联度一览表
2.2.3 专项技能系统模型的构建专项技能的模型构建主要是建立运动员专项技能的整体系统模型,是用灰色数学方法来反映运动员专项技能的整体构造。
灰色系统预测的具体方法[1-6]:
第一步,确定系统的主导因素和关联因素,并对各因素间的关系进行定性分析。这一步至关重要,是完成系统预测的基础。
第二步,建立GM模型群。对系统中的主导因素建立GM(1,1)模型,对关联因素建立GM(1,h)模型。
第三步,列出系统状态方程矩阵。
第四步,用龙格—库塔(Runge2Kntta)法,求解状态方程。
第五步,对方程解作累减还原,求得系统中各因素的预测值。
以世界纪录保持者赛布勒十项全能项目为例(表5)。
为减化运算过程,我们又将十项全能各项目分为:速度类、跳跃类、投掷类和耐力类四种素质因素[8]。由于这四种素质因素的发展都具有相对的独立性,因而我们视其为主导因素,分别建立GM(1,1)模型。而十项全能总分是由以上四种素质因素构成的,我们视其为关联因素,将建立总分与四种素质因素的 GM(1,h)模型[9]。
我们再将以上所得的模型群转化为系统状态矩阵,则有:

首先我们以2003年各因素实际值为参照对模型精度进行验证(见表6):

表6 塞布勒2003年十项全能水平的系统预测模型值与实际值对比
2.2.4 专项技能训练指标的定位对田径运动员专项技能指标建模预测的目的归结起来,就是要对运动员专项技能指标进行科学定位。也只有实现科学位,才能将灰色理论方法真正运用到运动训练实践之中。
实现对运动员专项技能训练指标的科学定位,需要采用两种灰色模型,即:GM(n,1)模型和GM(n,h)模型。
GM(n,1)模型为单变量模型,主要特征就是可预测性,即对所研究的变量可以进行超前规划。但系统中各因素不是孤立的,而单变量模型却将各因素间的关系隔离开,失去了系统的整体性。要研究系统多因素的整体规划问题就必须使用多变量模型,即GM(n,h)模型。然而,多变量模型不能直接进行预测研究,要实现系统的超前规划,就必须将两种模型结合起来共同完成[10]。
以我国优秀女子跳远名将关英楠的数据资料为例(表7),建立GM(n,h)系统状态基础模型。
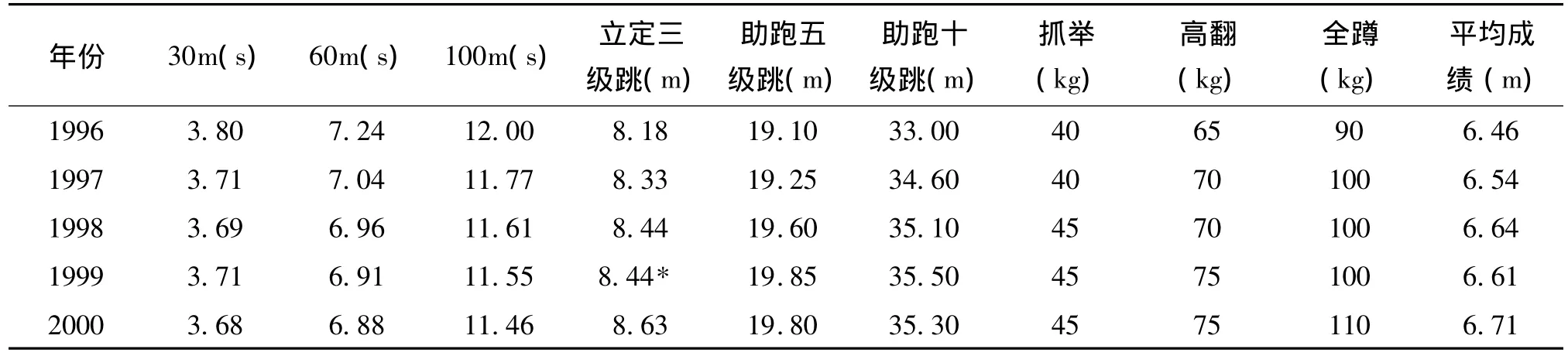
表7 1996~2000年关英楠各项指标成比赛成绩
这里我们采用最常用的一次累加方法,即:n=1。再将变量数设定为2,即:h=2。当然我们也可以选择更多的变量数,但如果我们选择更多变量参与到模型中来,为使方程有解就必须成倍地增加相应的辅助模型,从而会导致运算量成几何基数增长。
经计算得出:


检验结果:(表8)

表8 9个GM(1,2)模型的关联度检验结果
我们由关英楠近几年成绩可以发现,其年最佳成绩间的差距在20cm左右,如果想知道关英楠跳远超过7.00m时各指标应处的相应水平,就应该首先找出年平均成绩超过6.80m的年份。经GM(1,1)预测模型计算,2003年关英楠跳远的年平均成绩将可能达到6.84m,此时的模型维度为8,我们将成绩与维度值代入GM(1,2)系统状态基础模型中,结果(表9):

表9 关英楠跳远年平均成绩达到6.84m时的各指标相应水平
这样我们就完成了对运动员专项技能训练指标的初步定位。
由于灰色模型具备较好的动态规划特征,我们还可以对运动员专项技能指标做进一步分析和定位。即将各因素指标模型预测值与指标模型规划值进行进一步对比(见表10):

表10 指标模型规划值与预测模型值间的对比
由表10发现,按现这样的发展速度各指标达到相应的目标水平,30m需要14年;60m要3年;100m要3年;立定三级跳要2年;助跑五级跳要3年;助跑十级跳要4年;抓举、高翻已基本达到该水平;全蹲已超过这一水平。
可见,关英楠的跳远成绩要达到7.00m(年平均成绩达到6.80m),最关键的问题是如何提高其助跑的短距离加速能力,按现行的训练方式很明显无法达到这一指标,必须在训练方法、训练安排上加以改换和侧重。
3 结论
灰色系统理论与方法以其贫信息动态性特征,从根本上解决了田径运动员专项技能系统研究数据量严重不足的障碍,真正实现了完全依照运动员个体特征进行专项技能的优化分析和训练指标的科学规划。具体可从四个方面逐步展开。
(1)按照当前所处发展阶段的不同,选择GM(1,1)模型方法、GM(2,1)模型方法或 GM(1,1)残差模型方法建模,实现运动员专项技能趋势预测和培养目标的科学定位。
(2)采用带有时间发展特征的灰色关联分析方法,筛选出运动员专项技能的重点指标。
(3)建立专项技能灰色系统模型,确定运动员个体专项技能的整体状态。
(4)通过GM(n,1)模型和GM(n,h)模型对比,最终从模型仿真角度计算出训练实践所需达到的具体指标数值。
[1]刘思峰,郭天榜,党耀国,等.灰色系统理论及其应用[M].北京:科学出版社,1999.
[2]傅立.灰色系统理论及其应用[M].北京:科学技术出版社,1992.
[3]刘嘉津.解决转折期体育事件预测问题的GM(2,1)建模方法应用研究[J].天津体育学院学报,2006,21(3):252-254.
[4]张正红.我国女子链球运动员顾原各项素质和专项成绩的关系[J].湖北体育科技,2001,20(3):27-28.
[5]杨利勇.运用GM(1,N)模型对链球运动员顾原训练状态的分析研究[J].山东体育学院学报,2004,20(2):62-64.
[6]肖新平.灰色系统模型方法的研究[D].武汉:华中理工大学,2002.
[7]http://www.iaaf.2006-03-21/2006-04-27.
[8]卢刚,徐细根.中国与世界十项全能纪录保持者成绩特征对比分析[J].首都体育学院学报,2005,17(5):76-77.
[9]刘嘉津.体育复杂系统的灰色预测方法探析[J].中国体育科技,2007,43(1):113-115.
[10]刘嘉津,孙桂云.GM(1,h)系统状态模型在田径训练中的应用[J].上海体育学院学报,2003,27(1):78-81.
[11]张玉美.关英楠的身体训练[J].田径,2001,(4):12-13.

