全等三角形的实际应用

刘　顿

全等三角形源于生活,又为我们的生活服务. 请看下面三个例子.

一、测量河宽

例1如图1所示,要测量河宽AB,可先在岸上画AB的垂线段BC,并在BC上取点D,使BD=CD,再作BC的垂线CE,使A、D、E三点共线,最后量出线段CE的长就是AB的长,为什么?

简析:由于AB⊥BC,EC⊥BC,

所以∠B=∠C=90°.

在△ABD和△ECD中,

∠B=∠C,BD=CD,

∠ADB=∠EDC(对顶角相等),

所以△ABD≌△ECD(ASA).

所以AB=EC,即量出线段CE的长就是AB的长.

评点:数学建模是解决实际问题的关键.在本例中,运用了三角形全等寻找AB与CE的关系.

二、判断距离关系

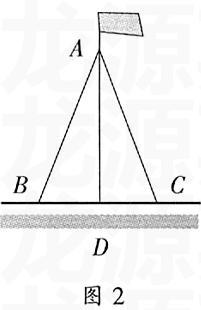
例2如图2所示,两根长度为10m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?为什么?请说明理由.

简析:两个木桩离旗杆底部的距离相等.

理由:因为AD⊥BC于点D,

所以∠ADB=∠ADC=90°.

在Rt△ADB与Rt△ADC中,

因为AD=AD,AB=AC,

所以Rt△ADB≌Rt△ADC.

所以BD=DC.

评点:本题运用了直角三角形全等的判定条件求解.

三、方案设计

例3图3为人民公园中的荷花池的示意图,现要测量此荷花池两旁A、B两棵树间的距离(不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.

要求:(1)画出你设计的测量平面图;

(2)简述测量方法,并写出测量的数据(长度用a、b、c、…表示;角度用α、β、γ、…表示);

(3)根据你测量的数据,计算A、B两棵树间的距离.

简析:测量AB的距离的方法很多. 这里用全等三角形的知识来解决,具体方案如图4所示.

一般步骤为:在地面上找可以直接到达A、B的点O;在AO的延长线上取一点C,使OC=OA;在BO的延长线上取一点D,使OD=OB;测得DC=a,则AB=a.

评点:这道开放型设计方案题,求解的方法很多. ■