“小把戏”的小魔术

王宝琪

魔术师大卫有个儿子,名叫小卫。因为在父亲身边长大,耳濡目染中小卫也学会了玩魔术,于是他常在小伙伴面前炫耀,不过玩的都是些“小把戏”。时间一长,伙伴们不再叫他小卫,而叫他“小把戏”了。这不,“小把戏”又在教室里玩起小把戏来了。

“各位,今天我要玩三个非常有趣的小魔术,而主要道具只是一些普通的纸条。不相信?那就瞪大眼睛瞧着吧!”

一、亲密的曲别针

如图1,将纸条折成“S”形,形成三层,用一只曲别针夹住前两层,再用另一只曲别针夹住后两层。

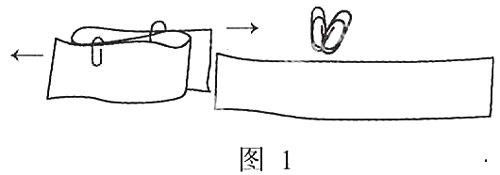
然后,拉住纸条的两头分别向两边拉,“啪”的一声,两只曲别针就从夹着的纸条上跳了出来,奇迹般地钩到了一起。奇怪吧?其实一点都不奇怪。这只是一种曲度转移的拓扑现象,当纸条被拉直时,它折叠的“S”形曲度就转移到曲别针上了。

二、剪不开反变长

如图2,将纸条的一端扭转半圈(即180°),用胶带把纸条的两端接在一起,成为一个纸环。然后通过中心线把纸环剪开。咦,纸环怎么没有变成两个纸环?竟然还是一个纸环!不过这个纸环有原来的两倍长!

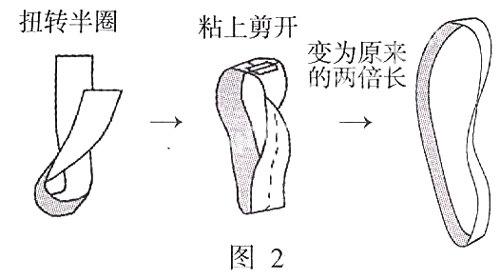
我们得到的这种纸环叫麦比乌斯环,它只有一面,不分上面和下面!不信你用铅笔沿着纸环画一条线试试,当你画完整个纸环时,会发现铅笔又回到了起点。

三、连环套

为什么上面的纸环剪开后还是一个环呢?我偏要叫它变为两个环!能不能做到呢?能!同样的纸条,同样的剪法,只是纸条的一头不是扭半圈,而是扭一圈(360°)就能办到了。如图3所示,就这么简单!

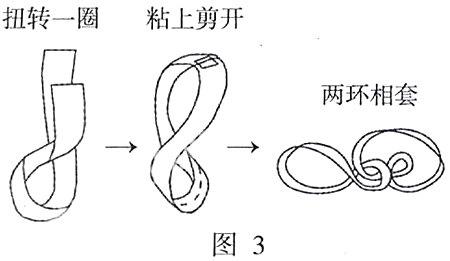
真是一个令人惊讶的结果。剪开后得到与原来同样长度的两个环,还相互套牢了!如果现在你再沿这两个环的中心线剪开,你又将得到大小与原来相同的全部套在一起的四个环!真是不可思议!

(编辑 孙世奇)