基于多智能体博弈的供应链配送网络协调优化模型研究
[摘 要] 供应链配送网络的流通效率是影响供应链绩效的关键因素。在运输能力有限的条件下,加快企业间的资源流通,促使配送网络最大限度地流通顺畅,对提高供应链整体绩效有着十分重要的意义。本文以多智能体技术为基础,利用博弈论的相关知识提出了供应链配送网络优化的协调模型,以求网络运输系统最终达到Nash均衡,从而较好地解决有限运输能力条件下的供应链配送网络的整体优化问题,达到整个配送网络的整体绩效最优。
[关键词] Agent;供应链配送网络;博弈协调;Nash均衡
[中图分类号]F270.7[文献标识码]A[文章编号]1673-0194(2009)01-0048-04
一、问题的提出
长期以来,供应链配送网络的设计与优化都是物流研究领域的重要课题。研究的内容主要包括单一配送中心(Distribution Center,DC)选址方法和多个配送中心选址及分配方法两个方面[1]。人们也提出了很多著名的方法和模型来求解这些问题[2]。但是却很少考虑运输过程中,在运输能力有限的条件下如何最大限度地发挥运输效率的问题。配送网络的流通效率是影响供应链绩效的关键因素,发挥供应链配送网络最大流通效率解决方案的文献较少, 这些研究的主要方法是通过建立物流的数学模型,运用运筹学和最优控制理论来控制和优化整个供应链配送网络。但由于供应链系统的复杂性、物流模型的局限性等因素,导致供应链优化控制的效果不理想。
具有自主性、移动性、协作性等特点的智能体(Agent)为供应链配送网络这个复杂的大系统开辟了新的解决途径,基于多智能体的供应链系统已成为一个研究热点。区域协调是基于多智能体的供应链配送网络协调的一个主要问题,它是指在运输能力有限的条件下, 根据不同的运输策略,均衡某几个节点企业所组成的小区域的运输量,从而提高整个供应链配送网络的流通能力。它要求各小区域间的良好协作,而现实中的供应链配送网络是由利益相对独立的多个企业通过联盟或合作关系组成的,为实现整个供应链配送网络的协调必然会引起各小区域之间一定程度的冲突。因此,如何解决这些冲突是急需解决的重要问题。博弈论是研究理性的主体之间冲突及合作的理论,它研究主体的行为是如何相互影响的,主体是如何在相互作用中做出自己的行为选择和行为决策的[3-5]。用博弈论的方法来分析问题,使问题的研究不仅局限于站在某个决策方的立场上找出针对其他方的对策,更重要的是在分析这些决策过程时能够发现各方相互制约、相互作用的规律,从而导出合理的结果并用以解决相应的实际问题[6]。将供应链配送网络上的各个仓库、配送中心、中转仓库、分销商、零售商等都看成是一个个的中转站,而将原材料、装配件、半成品、成品等都看成是运输的资源,使供应链上的全部资源在配送网络中最大效率地流通顺畅。
二、Agent代理供应链配送网络系统的运作机理
配送网络是由多个单元构成的,基本的单元包括仓库、配送中心、中转仓库、分销商、零售商等,这些单元可以称为子系统[7],这些子系统当中任何一个或几个结合起来都可以构成一个配送网络。这些不同的单元共同构成了配送网络不同的具体内容和功能。所有这些单元互相区别又互相联系,它们既是不同的单元,彼此又互相联系着。由它们的互相区别性,可以各自发挥自己的特长,由它们的互相联系性,又可以起到互相协作、互相补充的效果。根据单元在配送网络上所处的位置,可以把整个的供应链配送网络分成一个个的区域,而每个区域又分成一个个的单元,在每个区域内的单元都是交互的。因此,多Agent供应链配送网络协调系统主要包括两类Agent:由单个单元组成的单元Agent和由几个单元所组成的区域Agent。
每个Agent主要包括3个层次[8]:通信层、协作层和控制层。通信层由通信模块构成,主要完成与其他Agent的信息交互;协作层由学习机、推理机、规则库和知识库4个部分组成,主要完成和其他Agent进行协调并生成最终决策的功能;控制层由控制模块构成,主要完成指导控制任务,并将控制任务的信息通过通信层传递给其他Agent。
所有的单元Agent和区域Agent都有着共同的全局目标——使得整个配送网络绩效最优。而又有自己的局部目标——尽量使本单元利润最大(或是本区域利润最大)。单元Agent之间,单元 Agent与区域Agent之间,区域Agent之间是相互影响、相互作用的,因此,每个Agent的决策必然要受到另一些Agent策略选择的影响,Agent之间必然会发生一定程度的冲突。下面应用博弈论的相关知识,建立基于Agent的供应链配送网络系统运输模型,实现博弈均衡,实现配送网络的整体运输效率最大,以提高整个供应链系统的绩效。
三、供应链配送网络系统协调优化模型
1. 基本符号和定义
为建立供应链配送网络运输系统的协调模型,引入以下符号和定义:
(1)将每个单元都看成是中转站,在某一时段内要运出的资源数量是一定的,运输能力也是一定的。用东、西、南、北4个方向表示资源要运去的4个其他单元。Qi(t)表示t时段内等候在第i个单元的产品数量的向量。Qi(t)=
{Qi,E(t),Qi,S(t),Qi,W(t),Qi,N(t)},Qi,E(t),Qi,S(t),Qi,W(t),Qi,N(t)分别表示t时段内等候在i单元的运往东、南、西、北4个单元的资源数。
(2)Qi表示第i单元的资源数值的向量,Qi ={Qi,E,Qi,S,Qi,W,Qi,N},Qi,E,Qi,S,Qi,W,Qi,N分别表示运往不同单元的等候资源的数量值,可以根据具体情况进行修改。
(3)A表示博弈协调中的行为和决策Agent,它的目的是通过选择行动策略以最大化自己的效用水平,是所有Agent的集合。A={Agent1,Agent2,…,Agent n}。
(4)I表示每个Agent拥有的信息,包括其他Agent的特征和行动策略的信息。
(5)S表示Agent的所有可能的策略或行动的集合,一个Agent的全部可行策略称为它的策略空间。每个Agent有一个纯策略的有限集,为了表示有限运输能力和运输的有序性,运输策略S只取4种策略,S={东西直运、南北直运、东西双左运、南北双左运}。例如:东西直运表示在东西方向等待的资源运往东西两个单元,那么运往南北两个单元的资源要继续等待。东西双左运表示在东西方向等待的资源分别运向南北两个单元,而南北方向的单元要继续等待。在每个方向上运输能力也是有限制的,用阈值表示,阈值就是每个方向上可运输资源的最大量。阈值可根据具体情况进行修改。
(6)U表示Agent获得的利益,是指在既定策略组合条件下Agent的得失情况,即在一个特定的组合下得到的效用水平。U为Qi(t)的收益函数。收益即是排队的资源数。排队的资源数越少,效用水平越高。
(7)Nash均衡:设有n个Agent的博弈描述为G={A,S,U},若此问题中战略组合S*={S1*,S2*,…,Sn*}是一个纳什均衡,则必须满足Ui(Si*,S- i*)≥Ui(Si,S- i*),?坌si∈Si,式中:Si*表示第i个Agent选择的战略;S- i*表示除i之外的所有Agent的策略组成的向量;Ui表示第i个Agent的效用水平;Si表示第i个Agent的策略空间。
2. 协调模型[9]
一个Agent的决策会影响其他Agent的决策,同时,也受其他Agent决策的影响,因此,一个Agent在做决策时,应考虑其他Agent可能采取的战略来决定自己的战略。通过Agent间的相互通信,每一个Agent对其他Agent的特征(策略空间、效用函数等)有完全的了解,这决定了Agent间的协调过程是基于完全信息的博弈过程。一次博弈协调,定义为G={A,I,S,U},式中:A={Agent1,Agent2,…,Agent n},I表示每个Agent拥有的信息,S={东西直运、南北直运、东西双左运、南北双左运},U为Qi(t)的收益函数。每个Agent依据它所拥有的信息I,在S中选择合适的策略,通过不断的协调,使它们的盈利达到纳什均衡,即:
Ui(Si*,S- i*)≥Ui(Si,S- i*),?坌si∈Si。(式1)
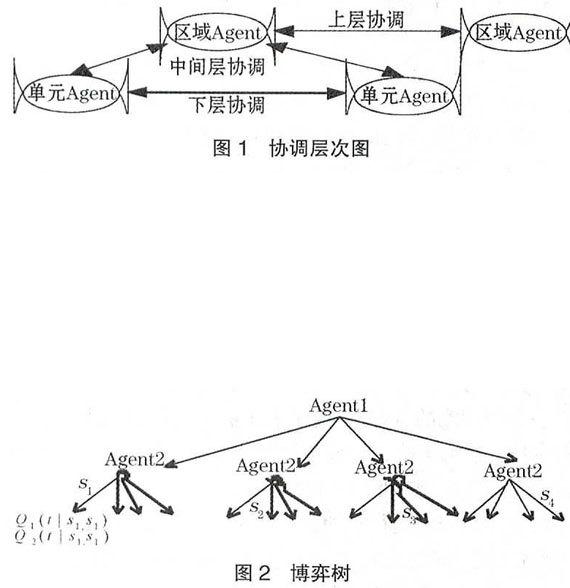
整个协调过程分为3个层次:下层是单元Agent与其相邻的单元Agent之间的协调;中间层是区域Agent与单元Agent之间的协调;上层是区域Agent与其相邻的区域Agent之间的协调。如图1所示。
3. 协调算法:Q2(T | s1,s1)
第一步,单元Agent的资源排队数超过阈值,则向相邻的单元Agent发出请求。
第二步,相邻的单元Agent响应请求,并构建如图2所示的博弈树(博弈树分枝上的字母代表Agent的策略),根据式1寻找Nash均衡。
第三步,如果Nash均衡存在,则Agent的行动策略就是达成Nash均衡时的策略,每个Agent按照该策略控制单元策略,本次协调结束。如果没有Nash均衡,则向该单元Agent所在的区域Agent发出请求。
第四步,区域Agent响应请求,对其所管辖的单元Agent进行博弈协调,寻求Nash均衡,如果Nash均衡不存在,则该区域Agent向相邻的区域Agent发出请求。
第五步,相邻的区域Agent响应请求,进行博弈协调,寻求Nash均衡,如果Nash均衡不存在,协调失败,则每个Agent保持原先的策略不变。

四、计算案例
用图3所示的一个简单供应链配送网络来说明上面的协调算法。Agent 1、Agent 2、Agent 3分别是3个单元Agent,它们由区域Agent管辖。为分析方便,每个Agent的策略集为S={东西直运、南北直运、东西双左运、南北双左运}。图中的数字为t0时段内各个单元向各个方向等待运送的资源数。
由于运输能力有限,当等待的资源数超过阈值时,单元 Agent间就要进行协调。在t0时段西口的排队产品数
Q2,W(t0)=19,大于阈值QW(设QW=15),则Agent 2向Agent 1发出请求,Agent 1响应请求并进行博弈协调,博弈协调的收益即是排队资源数,它是Agent 1、Agent 2博弈协调的目标和得失情况的体现,收益的多少取决于它们的策略组合。假设每个运货周期,到达单元的每个方向的资源数为λ,可运往到各单元的资源数为μ,并假设μ =1.5λ,那么单元1和单元2在t1时段的排队资源数是由在t0时刻采取的策略决定的。通过构建博弈树可以知道有以下的4种情况:
(1)Agent 1,Agent 2都选择s1,两个单元的资源数分别是15+2λ,13+3.5λ。
(2)Agent 1选择s1,Agent 2选择s2,两个单元的资源数分别为15+2λ,25+2.5λ。
(3)Agent 1选择s2,Agent 2选择s1,两个单元的资源数分别为16+2.5λ,13+2λ。
(4)Agent 1,Agent 2都选择s2,两个单元的资源数分别为16+λ,25+λ。
当λ<12时,Agent 1,Agent 2都选择s1,达到Nash均衡;当λ>12时,Agent 1,Agent 2都选择s2,达到Nash均衡。Agent 1,Agent 2根据其相应的策略控制单元。以上介绍的是下层协调,如果单元3南口的资源排队数Q3,S(t0)等于18而不是图中所示的9,那么Q3,S(t0)大于阈值QS(设QS=15),则Agent 3向Agent 2发出请求,而此时Agent 2也向Agent 1发出请求,这种情况下Agent 3和Agent 2,Agent 2和Agent 1之间的Nash均衡很难达到。于是它们向区域Agent发出请求,区域Agent响应请求并进行博弈协调,开始中间层协调。
通过搜索博弈树可知,当Agent 1选择策略s2,Agent 2选择策略s2,Agent 3选择策略s2,达到Nash均衡。上层协调与下层协调类似。
通过区域Agent与区域Agent间的协调,可以使在各个单元等候的资源数达到最少,从而可以最大限度地使资源在整个配送网络上流通顺畅。
五、结束语
供应链配送网络是配送过程中相互联系的组织与设施的集合。它的最终目的是为了使最终顾客满意,从而实现整个供应链的价值,并增强供应链的竞争能力。但是因为配送网络中的元素是属于不同实体所有的,这些不同实体之间都有着自己的利润和风险,因此它们会从自己的利益出发,采取相应的措施使自己利润最大化。一方做出的看来合理的决策有可能会对整个系统带来很大的影响。因此,在进行配送网络协调时就要把供应链的协调和整合机制作为指导思想,从而把供应链中的不同实体作为一个整体来进行协调。
用Agent技术来协调供应链配送网络,就可以发挥系统协调整合的优势。每一个配送网络都是—种有机结合体,而不是一个组合体。系统各个单元之间变成一种互相联系、不可分割的关系,只有这样才能互相协调力量。使系统的整体功能大于各个单元功能之和。只有这样,供应链配送网络的协调才能从整个系统的角度进行较为全盘的优化。
主要参考文献
[1] 李延晖,马士华,刘黎明. 基于时间约束的供应链配送系统随机模型[J]. 预测,2004(4).
[2] 日通综合研究所. 物流手册[M]. 吴润涛,等,译. 北京:中国物资出版社,1986:226-245.
[3] Martin J Osborne,Ariel Rubinstein. 博弈论教程[M]. 魏玉根,译. 北京:中国社会科学出版社,2000.
[4] 施锡铨. 博弈论[M]. 上海:上海财经大学出版社,2000.
[5] Fei Yue Wang. A Coordination Theory for Intelligent Machines[D]. Rensselaer Polytechnic Institute,1990.
[6] 陈进. 论区域博弈分析的方法研究[J]. 管理科学,1999(4):66-68.
[7] 任春玉,王晓博,李子群. 基于供应链的物流配送网络模型研究[J]. 哈尔滨商业大学学报:自然科学版,2006,22(4).
[8] 陈森发. 复杂系统建模理论与方法[M]. 南京:东南大学出版社,2005:42-43.
[9] 李振龙,陈德望. 交通信号区域协调优化的多智能体博弈模型[J]. 公路交通科技,2004,21(1).

