数学课堂重在培养学生的思维能力
洪建蕊 胡公胜
摘要:发展学生的数学能力,是数学教师进行数学教学的重要目标,也是学生能真正学好数学最重要的任务。数学能力包括数学观察能力、数学记忆能力和数学思维能力等,而最重要的是数学思维能力。本文就现在教学中存在的问题及如何利用数学课堂培养学生的思维能力展开论述。
关键词:思维;数学;过程
现代教育理念告诉我们,让学生学会学习比学会知识重要得多。经验的获得,必须由学生通过实践,自己感悟——内化。数学课程标准在具体教学目标的阐述中,多次提到要“经历……过程”。只有多让学生经历数学知识产生、形成、发展和应用的过程,让他们尝试成功与失败,才会使他们逐步积累自己的经验,并能运用这些经验与当前信息相互作用,有效地去自主解决问题,从而培养学生主动参与数学活动,提高学生的学习能力。然而,在现实课堂中我们数学老师往往为了完成每一节数学课的数学知识教学,而忽略了学生的思维暴露过程,缺乏对学生的创造性学习的培养。如下面的一节课就让我感触颇深。
这是一堂一元一次方程解应用题第二课时公开课,因为在第一课时学生已基本会列方程解简单应用题,所以A老师先出示一个调配问题,待学生解完,教师出示下题(如下图):一标志性建筑的底面呈正方形,在其四周铺上花岗岩,形成一个边宽为3米的正方形框。已知铺这个框恰好用了192块边长为0.75米的正方形花岗岩(接缝忽略不计),问标志性建筑底面的边长是多少?
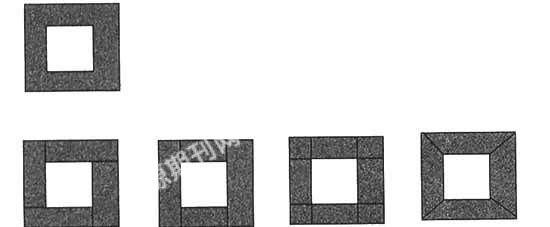
题目一给出,A老师便问有几种不同分割方法求面积?然后让学生讨论。此时大部分学生一片混乱,为什么要分割,到底设什么,求哪一部分的面积,学生并不清楚。过了好久,A教师总算从学生中找到了一种方法:将阴影部分分成四个相同的长方形(如下图),设标志性建筑底面的边长是x米,列出方程得:4×3(x+3)=192×0.752,随后A老师又投影,显示了以下几种分割方法。
A老师的出发点是好的,她想开放课堂,给学生更多的空间。但A老师一拿出例题不做任何分析,好多学生不知道题中要求图中大正方形的边长还是求小正方形的边长(这节课我上过,有好多学生误以为求大正方形的边长)。最后老师拿学生的作品放映就结束此例,对好多中下学生而言思绪一片混乱,为了公开课的效应而不顾及学生的接受情况,我们付出的代价是惨重的。更何况,就算是优秀生对此题的理解,也是利用大正方形的面积减去小正方形的面积等于192块花岗岩的面积来列方程。所以我认为老师拿出本题应留一定的时间让学生理解题意,达成共识,设标志性建筑底面的边长是x米(也就是小正方形的边长为x米)后,再让学生讨论该如何列方程求解。这样学生就很可能会列出方程:(x+6)2-x2=192×0.752,此时我们就可以让学生大胆尝试解该方程,当学生发现自己还不会解此方程时(因为还没学过完全平方公式),教师可引导学生:既然用整体表示阴影部分面积列出的方程不会求解,还能用什么方法来表示阴影部分的面积?这时学生应该会想到分割的方法。这样打破教材,充分暴露了学生思考问题的思维过程,尽管第一种方法用现在已学的知识还未能解决,学生感到暂时失败,但这种方法将来更实用,这样设计至少为学生后续学习创造了条件。在以后的学习中让学生体会到掌握一种方法比获得知识更重要。
“教学过程是师生双方有目的有计划地以教材为中介,通过教师的教和学生的学共同完成预定任务的统一活动过程。”但是,在教学实践中,中学生学的活动的“有目的”性往往是缺乏的,从目前我国的实际情况出发,重要的是在数学课堂中去体现问题解决的精髓。为此在数学课堂教学中应做到以下几点:
1. 鼓励学生大胆去探索、猜想、发现
要培养学生的思维能力,首先是要让学生具有积极探索的态度,猜想、发现的欲望。教材要设法鼓励学生去探索、猜想和发现,培养学生的问题意识,经常地启发学生去思考,提出问题。学生学习的过程本身就是一个问题解决的过程。当学生学习一门崭新的课程、一章新的知识乃至一个新的定理和公式时,对学生来说,就是面临一个新问题。在教科书中经常提一些启发性的问题,就会让学生逐步养成求知、好问的习惯和独立思考、勇于探索的精神。无论是教科书的编写还是实际教学,在讲到探索、猜想、发现方面的问题时要侧重于“教”:有时候可以直接教给学生完整的猜想过程,有时候则要较多地启发、诱导、点拨学生。当然不要在任何时候都让学生亲自去猜想、发现,那么课堂会散而乱。
2. 打好基础
要解决任何一个问题,必须有相关的知识和基本的技能。当人们面临新情境、新问题,试图去解决它时,必须把它与自己已有知识联系起来,当发现已有知识不足以解决面临的新问题时,就必须进一步学习相关的知识,训练相关的技能。应看到,知识和技能是培养问题解决能力的必要条件。在提倡问题解决的时候,不能削弱而要更加重视数学基础知识的教学和基本技能的训练。教给学生哪些最重要的数学基础知识和基本技能,是问题的关键。
3. 创设好问题、好情境
问题设计得好就能很好地激发学生去思考问题,课堂上才能让大部分学生思维活跃起来。因为一个好问题或者说一个精彩的问题应该有如下的某些特征:(1)有意义,或有实际意义,或对学习、理解、掌握、应用前后数学知识有很好的作用;(2)有趣味、有挑战性,能够激发学生的兴趣,吸引学生投入进来;(3)易理解,问题是简明的,问题情境是学生熟悉的。
另外,数学包括两个层面,一是有形的数学知识这一物质层面,一是无形的数学思想方法的精神层面。精神层面的思想、方法只有在数学活动过程展开中才能体现。教学的思想方法要比具体的数学知识重要得多、意义也深远得多。因此,传授数学知识,进行数学活动必须把精神层面展示出来,这样的教学才算是有价值的。但是,在数学课堂中能供数学教师操作的是具体的、有形的数学知识,而数学知识又是形式化的。形式化的东西具有简约性与概括性。因此,教师操作起这些形式的东西就往往感到简单、方便,追求纯形式,而忘记了对学生来说这些却成了他们的“负担和约束”,忘却了这“简单”背后的应用的“复杂”,“方便”背后的理解上的“艰难”。
总之,从着眼于人的发展出发,探索性的学习方式应成为学生学习数学的主要方式。探索必须建立在学生的主观愿望和知识经验的基础上,必须让学生经历一系列“观察、操作、讨论、交流、猜测等等的体验活动,让学生的思维真实的充分暴露出来,才能达到真正理解和掌握基本的数学知识与技能、数学思想方法,同时获得广泛的数学活动经验。”数学课程标准中强调经历从不同角度研究同一问题的过程,如果我们能灵活使用教材,把教材上的内容开放地呈现给学生,就能使学生有更多的个性选择,为他们创新活动的开展提供更多的可能。
(乐清市虹桥镇第六中学)

