高速数字系统的串扰问题分析

吴　昊　陈少昌　王杰玉

摘 要：在高速数字电路设计中,信号完整性问题越来越突出,已经成为高速电路设计工程师不可避免的问题。串扰问题是信号完整性问题中的重要内容。分析串扰产生的机理,讨论各种影响串扰的因素,建立了两线串扰模型并采用Mentor Graphic公司的信号完整性分析软件Hyperlynx进行了仿真实验。仿真结果表明：耦合长度、线距、信号的上升时间以及介质层对两线之间的串扰都有直接影响,在仿真研究的基础上针对以上因素的影响提出减小串扰的有效措施。

关键词：高速数字电路；信号完整性；串扰；Hyperlynx

中图分类号：TN710 文献标识码：A

文章编号：1004-373X(2009)01-170-04

Crosstalk Analysis for High Speed Digital System

WU Hao,CHEN Shaochang,WANG Jieyu

(Naval University of Engineering,Wuhan,430033,China)

Abstract：Signal integrity has become a problem what cannot be ignored by designers in the high speed digital design.As one of the problems of signal integrity,crosstalk is analyzed in this paper.Then one module is found for it and simulated using Hyperlynx,software for signal integrity analysis of Mentor Graphic.Various factors such as the coupled length,signal rise time and the dielectric layer of crosstalk between the two lines has a direct impact are discussed,based on the results,and efficient measures are put forward to reduce crosstalk.

Keywords：high speed digital circuit;signal integrity;crosstalk;Hyperlynx

随着电子技术的不断发展,在高速电路中信号的频率的变高、边沿变陡、电路板的尺寸变小、布线的密度变大,这些因素使得在高速数字电路的设计中,信号完整性问题越来越突出,其已经成为高速电路设计工程师不可避免的问题。串扰是指有害信号从一个网络转移到另一个网络,它是信号完整性问题中一个重要问题,在数字设计中普遍存在,有可能出现在芯片、PCB板、连接器、芯片封装和连接器电缆等器件上［1］。如果串扰超过一定的限度就会引起电路的误触发,导致系统无法正常工作。因此了解串扰问题产生的机理并掌握解决串扰的设计方法,对于工程师来说是相当重要的。

1 串扰问题产生的机理

串扰是信号在传输线上传播时,由于电磁耦合而在相邻的传输线上产生不期望的电压或电流噪声干扰,信号线的边缘场效应是导致串扰产生的根本原因［1］。为了便于分析,下面介绍几个有关的概念。如图1所示［2］,假设位于A点的驱动器是干扰源,而位于D点的接受器为被干扰对象,那么驱动器A所在的传输线被称之为干扰源网络或侵害网络(Agreessor),相应的接收器D所在的传输线网络被称之为静态网络或受害网络。静态网络靠近干扰源一端的串扰称为近端串扰(也称后向串扰),而远离干扰源一端的串扰称为远端串扰(或称前向串扰)。由于产生的原因不同将串扰可分为容性耦合串扰和感性耦合串扰两类。

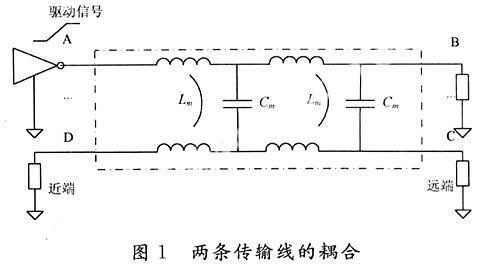
1.1 容性耦合机制

当干扰线上有信号传输时,由于信号边沿电压的变化,在信号边沿附近的区域,干扰线上的分布电容会感应出时变的电场,而受害线处于这个电场里面,所以变化的电场会在受害线上产生感应电流。可以把信号的边沿看成是沿干扰线移动的电流源,在它移动的过程中,通过电容耦合不断地在受害线上产生电流噪声。由于在受害线上每个方向的阻抗都是相同的,所以50%的容性耦合电流流向近端而另50%则传向远端。此外,容性耦合电流的流向都是从信号路径到返回路径的,所以向近端和远端传播的耦合电流都是正向的。

对于近端容性耦合串扰,随着驱动器输出信号出现上升沿脉冲,流向近端的电流将从零开始迅速增加,当边沿输入了一个饱和长度以后,近端电流将达到一个固定值。另外,流向近端的耦合电流将以恒定的速度源源不断地流向近端,当上升沿到达干扰线的接收端,此上升沿会被接受吸收,不再产生耦合电流信号,但是受害线上还有后向电流流向受害线的近端,所以近端的耦合电流将持续两倍的传输延迟。

对于远端容性耦合串扰,由于信号的边沿可看成是移动的电流源,它将在边沿的附近区域产生经互容流进受害线的耦合电流,而产生的耦合电流将有50%与干扰线上的信号同向而且速度相同地流入远端,因此随着干扰线上信号的传输,在受害线上将不断地产生的前向耦合电流而且和已经存在的前向耦合电流不断地叠加,并一同传向远端。由于串扰只在信号的边沿附近区域产生,流向远端的耦合电流的持续时间等于信号的跃变时间。具体的容性耦合如图2所示［3］。

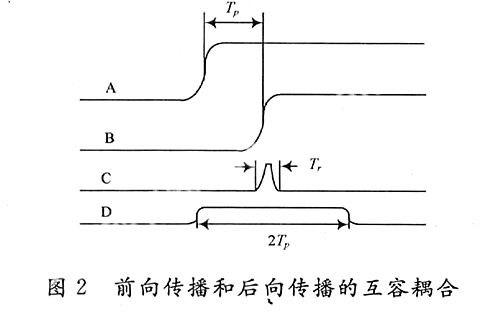
1.2 感性耦合机制

当信号在干扰线上传播时,由于信号电流的变化,在信号跃变的附近区域,通过分布电感的作用将产生时变的磁场,变化的磁场在受害线上将感应出噪声电压,进而形成感性的耦合电流,并分别向近端和远端传播。与容性耦合电流不一样的是,感性耦合电流的方向与干扰线上信号传播的方向是反向的,向近端传输时,电流回路是从信号路径到返回路径,而向远端传输时,电流回路则是从返回路径到信号路径。

对于近端感性耦合串扰,其特征与近端容性耦合串扰非常相似,也是从零开始迅速增加,当传输长度大于等于饱和长度以后,将稳定在一个固定值,持续时间是两倍的传输延迟。因为流向近端的感性耦合电流与容性耦合电流同向,所以两者将叠加在一起。

对于远端感性耦合串扰,感性耦合噪声与干扰线上信号边沿的传播速度相同,而且在每一步将会耦合出越来越多的噪声电流,持续的时间等于信号跃变的时间。但是由于电流流向与远端容性耦合电流是反向的,所以到达受害线远端接收器的耦合电流是两者之差。具体的感性耦合如图3所示［3］

1.3 互感和互容的混合效应

一般地,在完整的地平面上,容性和感性的耦合产生的串扰电压大小相等,因此远端串扰的总噪声由于容性和感性耦合的极性不一样而相互抵消。在带状线电路更能够显示两者之间很好的平衡,其远端耦合系数极小,但是对于微带线路,由于与串扰相关的电场大部分穿过的是空气,而不是其他的绝缘材料,因此容性串扰比感性串扰小,导致其远端串扰系数是一个小的负数［3］。

2 串扰的仿真分析

在实际的设计中,板层特性(如厚度,介质常数等)以及线长、线宽、线距、信号的上升时间等都会对串扰有所影响。下面结合使用Mentor Graphic公司的信号完整性仿真软件Hyperlynx,对上述的影响串扰的因素进行分析。首先在Hyperlynx中建立两线串扰的模型,如图4所示,设两线的线宽为5 mil,线长为6 in,线距为5 mil,两线均为顶层微带线,特性阻抗为49.5 Ω,两线都端接50 Ω的电阻,以消除反射的影响。干扰线的驱动器采用CMOS工艺器件的IBIS模型,电压为 3.3 V,频率为100 MHz。PCB的介电常数为4.3,六层板,其叠层结构如图5所示。

2.1 耦合长度对串扰的影响

改变两线的耦合长度,分别将耦合长度设置为 3 in,6 in,10 in,其他设置不变。

图6(a)是耦合长度为3 in的串扰波形,其中近端串扰峰值为126.34 mV,远端为43.01 mV；图6(b)是耦合长度为6 in的串扰波形,其近端串扰峰值为153.23 mV,远端为99.46 mV；图6(c)是耦合长度为10 in的串扰波形,其近端串扰峰值为153.23 mV,远端为163.98 mV。

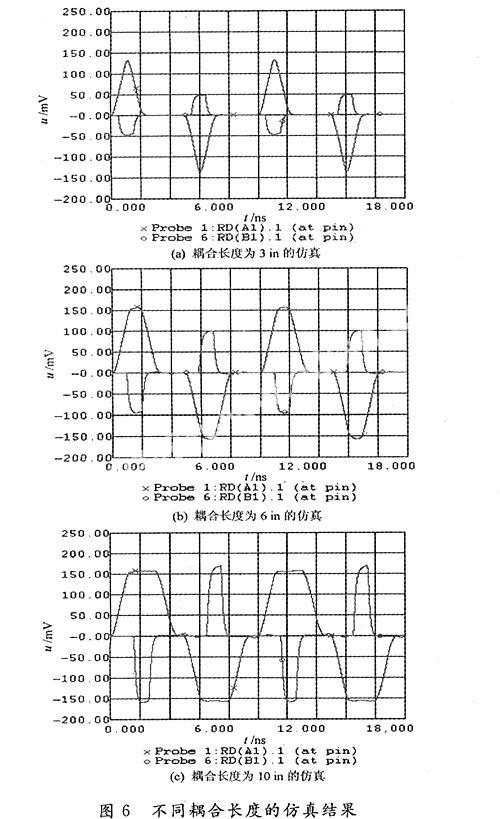
由此可见,对于远端串扰峰值与耦合长度成正比,耦合长度越长,串扰越大；而对于近端串扰,当耦合长度小于饱和长度时,串扰将随着耦合长度的增加而增加,但是当耦合长度大于饱和长度时,近端串扰值将为一个稳定值。

2.2 线间距对串扰的影响

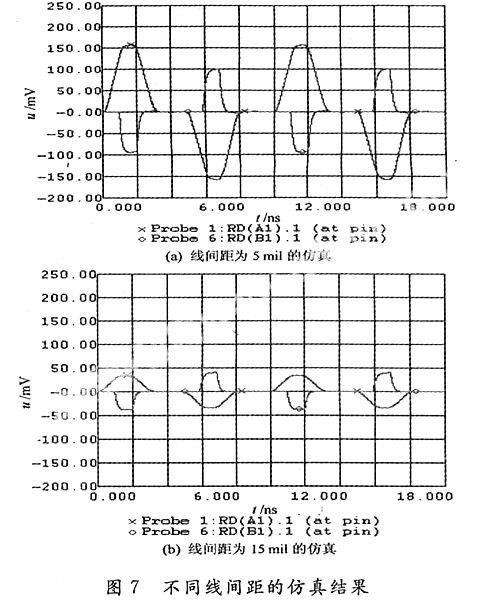
以下是保持其他设置不变,考察线间距的改变对串扰的影响。分别设置线距为5 mil,15 mil,仿真波形如图7所示。

由图7可知,当线间距为5 mil时,近段串扰峰值为153.23 mV,远端为99.46 mV；而线间距为15 mil时,近端串扰峰值为33.40 mV,远端为40.49 mV。可见随着线间距的增大,无论是近端还是远端串扰都将减小,当线间距大于等于线宽的3倍时,串扰已经很小。

2.3 上升时间对串扰的影响

下面考察上升沿时间的变化对串扰的影响,其他设置保持不变。分别设置驱动器为CMOS 3.3 V MEDIUM;CMOS 3.3 V FAST;CMOS 3.3 V ULTRA-FAST,仿真波形如图8所示。

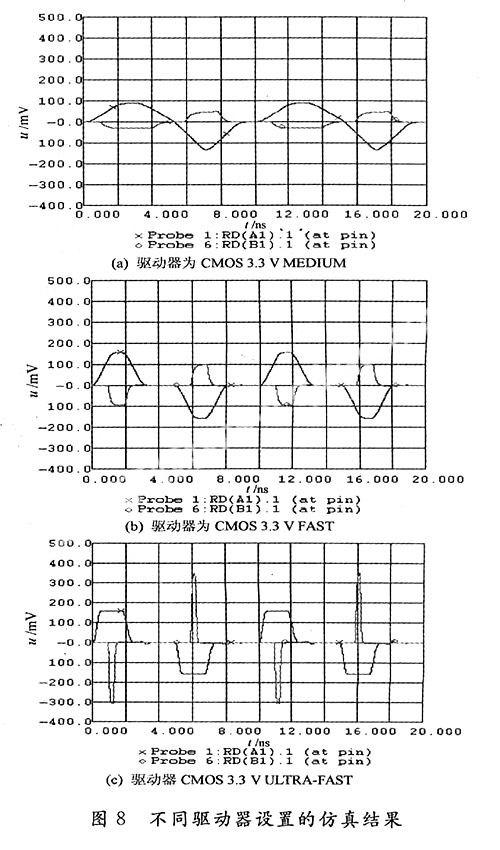
图8(a)中的近端串扰峰值为153.9 mV,远端串扰为46.3 mV；图8(b)中近端串扰峰值为153.2 mV,远端串扰为99.5 mV；图8(c)中近段串扰峰值为 153.2 mV,远端串扰为349.9 mV。可见,当上升沿时间缩短时,远端串扰噪声越来越大。对于近端串扰来说,如果与传输线的时延相比,上升时间较短,则近端串扰与上升时间无关；而如果与传输线时迟相比,上升时间较长,则近端串扰噪声与上升时间有关(随着上升沿时间的减小,近端串扰变大)［4］。

2.4 介质层厚度对串扰的影响

在PCB的叠层编辑器中将介质层厚度分别设置为 3 mil和6 mil,其他设置不变,仿真波形如图9所示。

考察以上的仿真波形可知,当介质层厚度为3 mil时,近端串扰峰值为153.2 mV,远端串扰为99.5 mV；当介质层厚度为6 mil时,近端串扰峰值为277.3 mV,远端串扰为163.9 mV。可见,随着介质层厚度的减小,串扰也将变小。

3 解决串扰的方法

串扰在电子产品的设计中普遍存在,通过以上的分析与仿真,了解了串扰的特性,总结出以下减少串扰的方法：

(1) 在情况允许的情况下,尽量增大走线之间的距离,减小平行走线的长度,必要时采用jog方式走线。

(2) 在确保信号时序的情况下,尽可能地选择上升沿和下降沿速度更慢的器件,使电场和磁场变化的速度变慢,从而降低串扰。

(3) 在设计走线时,应该尽量使导体靠近地平面或电源平面。这样可以使信号路径与地平面紧密的耦合,减少对相邻信号线的干扰。

(4) 在布线空间允许的条件下,在串扰较严重的两条信号线之间插入一条地线,可以减小两条信号线间的耦合,进而减小串扰。

4 结 语

串扰是信号完整性中的重要内容,影响系统的时序、降低噪声容限,导致系统无法正常的工作。介绍了高速电路中串扰产生的机理,并通过仿真对串扰进行分析,得出串扰的大小与影响串扰相关因素的关系,在此基础上提出了一些减小串扰的方法,对于在高速高密度的电路设计中解决串扰问题有一定的指导意义。

参考文献

［1］Eric Bogatin.信号完整性分析［M］.李玉山,李丽平,译.北京：电子工业出版社,2006.

［2］乔洪.高速PCB串扰分析及其最小化［J］.中国集成电路,2007,16(4):35-38.

［3］Howard Johnson,Martin Graham.高速数字设计［M］.沈文,朱来文,陈宏伟,等译.北京:电子工业出版社,2007.

［4］Stephen H Hall,Garrett W Hall,James A McCall.高速数字系统设计［M］.伍微,译.北京:机械工业出版社,2006.

［5］吕飞燕,沙斐.PCB上串扰的耦合机理和优化分析模型［J］.电子与信息学报,2005,27(7):1 167-1 170.

［6］余学莉.数字电路设计的信号完整性分析［J］.合肥工业大学学报:自然科学版,2004,27(7):843-846.

［7］唐珏,董天临.数字电路中的信号完整性研究［J］.电子质量,2005(10):82-84,67.

［8］Bob Ross.IBIS Models for Signal Integrity Application［J］.Electrical Engineering Times,1996.12(3).

［9］陈思思.信号完整性分析中的串扰分析［J］.武汉理工大学学报:信息与管理工程版,2005,27(5):23-26,30.

［10］黄德勇,张扬,杨云志.高速电路设计中的信号完整性研究［J］.电讯技术,2004,44(2):149-151.

作者简介吴 昊 男,1980年出生,硕士研究生。研究方向为高速数字电路的信号完整性研究。

陈少昌 男,1962年出生,硕士生导师,教授。研究方向为高速数字电路的信号完整性研究。