数据挖掘技术在财务分析中的应用

赵　磊

[摘 要] 数据挖掘技术是多学科交叉的新兴技术,它是随着数据的大量积累以及市场竞争对信息与知识的迫切需求而产生和发展起来的,并逐渐成为人们关注的热点。它将传统的数据分析方法与处理大量数据的复杂算法相结合,为探查和分析新的数据类型以及用新方法分析旧有数据类型提供了令人振奋的机会。将数据挖掘技术应用于财务分析,不仅拓宽了财务分析的范围,而且还可以发现那些隐藏在财务报表数据中的信息,对于帮助管理层做出及时、适当的决策是很有价值的。

[关键词] 财务分析;决策树;聚类;关联分析

[中图分类号]F275;F232[文献标识码]A[文章编号]1673-0194(2009)02-0034-05

一、研究背景

数据挖掘技术主要应用于商业、医学、科研领域,着眼于海量数据集存储、检索与处理,目标是从繁冗复杂的数据对象中找出其相关性。诚然,大多数公司的财务分析所需要的一些数据相对有限,尚不能称得上“海量”,但是如果能从另一个角度去换位思考,或许能得到意想不到的效果,为更深层次的财务分析作准备。

当前,大多数公司的财务分析是用一些财务指标来反映本公司的经营情况,分门别类、分项列出,先总体、后局部,个别异常个别说明。这种分析方式是正确的,然而很多情况下财务人员会忽略数据的相关性,无法抓住问题的实质,进而影响财务分析的准确性、全面性。造成这样的情况,一是由于财务数据范围相对较小,容易根据一些财务指标直观上发现问题,这就往往使人们忽视管理与经营上的不足;二是财务人员的知识水平相对有限,无法从更深层次角度去分析报表数据。本文以某财产保险公司省级分公司2004年度财务数据为例,分别从决策树算法、聚类、关联分析等角度来阐述数据挖掘技术在财务分析中的应用。

二、数据集选择

本文使用的样本数据来自某财产保险公司省级分公司2004年所公布的财务报表数据。由于该公司车险所占比例较大,因此将车险赔付率指标列入其中,同时为方便计算,对个别数据进行了处理。具体数据集见表1。

三、决策树算法

决策树分类法是一种广泛使用的简单分类算法,具有直观、容易解释的特点,其冗余属性也不会对决策树的准确率造成不利的影响,即个别属性的差异对总体分析及决策不会造成太大的误差。决策树广泛用于分类、聚类和预测型建模方法,采用“分而治之”的方法将问题的搜索空间分为若干子集。在财务分析中使用决策树,不仅可以“化繁为简”,而且具有直观、易于快速发现问题的特点,给人耳目一新的感觉。

1. 用Hunt算法建立决策树

从原则上讲,对于给定的属性集,可以构造的决策树的数目能达到指数级。尽管某些决策树比其他决策树更准确,但是由于搜索空间是指数级的,找出最佳决策树原则上是不可行的。尽管如此,学者们还是开发了一些有效的算法,能够在合理的时间内构造出具有一定准确率的次最优决策树。这些算法通常都采用贪心算法,能够在合理的时间内构造出具有一定准确率的次最优决策树,Hunt算法就是一种这样算法,它是许多决策树算法的基础。

在Hunt算法中,通过将训练记录相继划分成较纯的子集,以递归方式建立决策树。设Dt是与结点t相关联的训练记录集,而Y={ y₁,y₂,…,y_n}是类标号,Hunt算法的递归定义如下:

(1)如果Dt中所有记录都属于同一个类y_t,则t是叶结点,用y_t标记。

(2)如果Dt中包含属于多个类的记录,则选择一个属性测试条件,将记录划分成较小的子集。对于测试条件的每个输出,创建一个子女结点,并根据测试结果将Dt中的记录分布到子女结点中。然后,对于每个子女结点,递归地调用该算法。

2. 算法演示

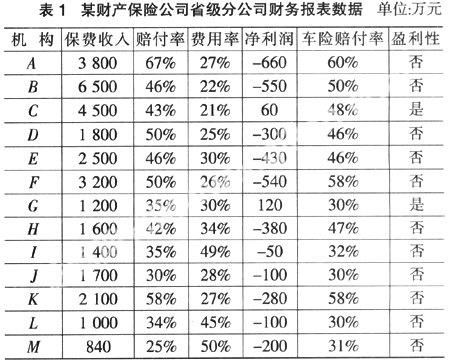
需要说明的是,本文将盈利性作为叶结点,主要是由于其属性只有“是”与“否”两类,可以简化算法的演示步骤,还可以从总体上发现公司各机构的利润情况,从而在一定程度上迎合了公司决策者的要求。此外,为方便说明,将每一步划分的机构情况也列入其中,但是这并不表明在实际应用中需要这么做。具体步骤如图1至图4所示。

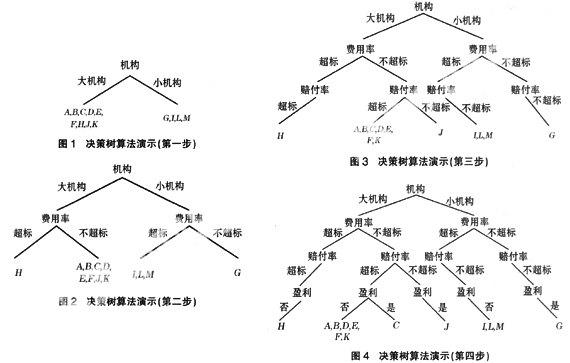
其中,大机构是指保费收入大于1 500万元的机构,小机构是指保费收入小于1 500万元的机构。

3. 对财务分析的启示

从图4中可以发现公司亏损主要集中在{A,B,D,E,F,K}与{I,L,M}等机构,它们占公司机构数目较大的比例。所以,公司下一步的经营治理计划应集中在这几个机构中。可以看出,决策树以图形方式给出较为直观、简洁的描述,不同于那种枯燥、冗长的文字描述形式。

四、聚类分析

聚类已经被广泛地应用于许多领域,例如生物学、信息检索、气象学、心理学、医学以及商业等诸多领域。通过对聚类的发现,我们可以找出在概念上有意义的具有公共特性的对象组,进而发现总体的特性。聚类分析根据在数据中发现的描述对象及其关系的信息,将数据划分成有意义或有用的簇(也可以称为组)。其目标是,簇内的对象相互之间是相似的(相关的),而不同簇中的对象是不同的(不相关的)。簇内的相似性(同质性)越大,聚类就越好。

在财务分析中,灵活运用聚类分析技术,对各种财务指标下的数据进行分组,可以方便找出其“由量变到质变”的临界点,为公司制定各类考核指标提供依据。对于簇内及簇间相似性的度量需要运用统计学中方差、标准差等概念,相对比较简单,不赘述。

1. K-均值算法

K-均值算法是一种迭代算法,迭代过程中不断地移动组集中的成员直至得到理想的组集为止。K-均值算法比较简单,也是一种最古老的、最广泛使用的聚类算法。虽然该算法的收敛准则不是基于平方误差来定义的,但它也可视为一种平方算法来度量各组内及组间的误差情况。利用K-均值聚类算法所得到的组,组内成员间的相似程度很高,同时不同组中成员的相异度也很高。给定组Ki ={t_i1,t_i2,…,t_im},则其均值定义为:

M_i= (t_i1+ t_i2+ …+t_im)/m。

在定义中假设每个元组仅有一个数值型属性值,而不是多个属性值,当然在财务报表中也不可能出现多个属性的数据。以下的算法描述了K-均值算法,但应注意簇均值的初始值是任意分配的,可以随机分配也可以直接使用前k个成员的属性值。此外,当没有元组(或很少的元组)被分配到不同的簇中时,就可以停止算法。也可以直接设置一个最大的迭代次数作为终止准则,使用最大迭代次数准则是为了在算法不收敛时也可以停止算法。

其基本算法如下:

(1)选择K个点作为初始均值,K是用户指定的参数,即所期望簇的个数;

(2)repeat;

(3)将每个点指派到最近的均值,形成K个组;

(4)重新计算每个组的均值;

(5)until 均值不发生变化。

2. 算法演示

为方便说明问题,我们选择赔付率与费用率作为数据集实验对象,并且将其分为3个簇,初始时按机构顺序选择前3个数值作为簇的均值。同时,利用比较欧几里得距离(差的绝对值)作为收敛参考准则,即将与均值距离最近的数值分配到该均值所代表的簇中去,如果存在于两个或多个均值距离相等,可以任意选择其均值所对应的簇。具体计算过程如表2、表3所示。

3. 对财务分析的启示

在表2中可以看出,作为聚类的机构集合{A,K},{B,C,D,E,F,H}与{G,I,J,L,M},如果该公司以赔付率35%作为考核要求,则A,K属于严重超标,B,C,D,E,F,H超标较多,只有G､I､J､L､M等机构合格｡但是,如若从数据挖掘角度出发,本期需对不同机构集合采取不同的惩奖措施,我们还可以设置50%与35%为动态临界指标作为下期考核经营业绩的依据,并且每期进行调整｡费用率可以参照以上进行分析,基本相同｡

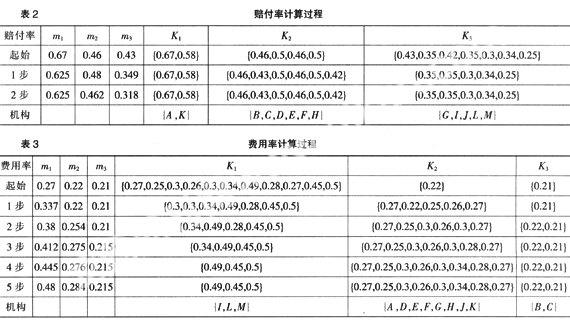
值得一提的是,我们还可以将以上两个不同聚类取交集得到一个二维聚类,即{A,K},{B,C},{I,L,M}｡对它们进行进一步的分析,可以综合得出哪些机构的财务指标是更为合理的,或者是极不合理的,为精确考核､计划提供依据｡

五､关联分析

许多商业企业在日复一日､年复一年的经营活动中积聚了大量的数据｡例如,某大型购物中心的结算系统每天收集大量顾客的数据｡零售商对这些数据的分析通常称作“购物篮”事务分析,以便了解顾客的购买行为,来支持各种商业应用,如市场促销､库存管理和顾客关系管理等｡

关联分析方法,用于发现隐藏在大型数据集中的令人感兴趣的联系｡所发现的联系可以用关联规则或频繁项集的形式表示｡例如,从大型购物中心销售终端所提供的数据中可以提出如下规则:

{奶粉,尿布,饼干}→{巧克力}

该规则表明奶粉､尿布和饼干与巧克力之间存在着很强的联系,因为许多购买奶粉､尿布和饼干的顾客也会购买巧克力｡商家可以使用这类规则,帮助他们发现新的交叉销售机会｡同样在财务分析中,我们可以根据感兴趣的财务指标进行内在数据挖掘,找出造成财务指标差异的原因｡

1. Apriori算法

Apriori算法是最著名的关联规则算法,已经为大部分商业产品所使用｡该算法利用大项目集性质,即大项目集的任一子集也一定是大的｡

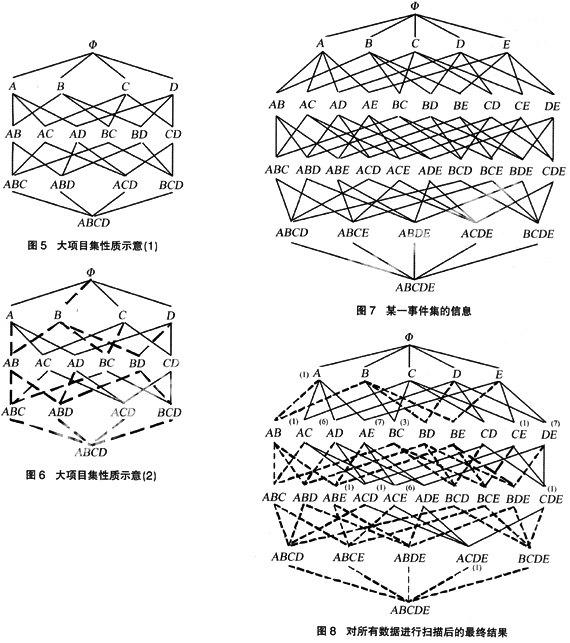
大项目集也被称为是向下封闭的,因为如果一个项目集满足最小支持度的要求,其所有的子集也满足这一要求｡其逆否命题也成立,即知道一个项目集是小的,它的子集也是小的｡可用图5和图6来展示这种重要的性质｡在这个例子中有4个项目{A,B,C,D}｡图中的线表示子集的关系,大项目集性质表明如果原来的项目集是大的,则在路径中位于其上面的任何集合也一定是大的｡在图中,ACD的非空子集是{AC,AD,CD,A,C,D}｡如果ACD是大的,则其每一个子集也是大的｡如果任何一个子集是小的,则ACD也是小的｡

Apriori算法的基本思想是生成特定规模的候选项目集,然后扫描数据库并进行计数,以确定这些候选项目集是否是大的｡由于在财务分析中,往往使用定性的方法去查找原因,这可以极大地提高Apriori算法效率｡比如管理层往往对利润亏损比较敏感,我们就可以直接以利润亏损这一财务指标为起点进行搜索计数､排序,只要查找一遍就可以找出频繁项集｡

2. 算法演示

从公司财务数据可以看出大部分机构亏损,为了找出公司亏损的内在原因,我们就以这一财务指标作为扫描的起点｡假定:

Φ =利润亏损;

A =大机构(机构保费收入>1 500万元);

B =小机构(机构保费收入≤1 500万元);

C =费用率超标(费用率>30%);

D =赔款率超标(赔付率>35%);

E =车险赔付率超标(赔付率>35%)｡

图7表示这一事件集的信息,图8表示对所有数据进行扫描后的最终结果,为方便说明,涉及的机构数标在指标上面｡另需说明,本文采用较高支持度的数据作为分析依据,排除了个别异常的干扰｡

3. 对财务分析的启示

根据关联分析得出如下结论:{大机构,赔款率超标,车险赔付率超标}→亏损,{小机构,费用率超标}→亏损,另由大项目集性质得出附加结论:{车险赔付率超标}→赔款率超标｡

为什么会得出以上结论呢?这需要深入分析公司的具体情况｡大机构亏损是由于其赔款支出过多这一原因造成的,说明大机构的规模与其效益不成正比,所担保的产品易于受损,属于典型的“越扩张就越亏损”｡而小机构情况则不同,由于成立初期需要消化的费用多,并且赔款效应尚未出现,因此造成了一定程度的亏损,但后期应高度重视保费质量｡其实,附加结论“{车险赔付率超标}→赔款率超标”所带来的问题更为严峻｡公司的大部分赔款支出来自车险,而车险是公认的亏损险种,这说明公司险种结构极为不合理,亟需改善险种结构,选择多元化营销来分散风险｡

六､结 论

最后,数据挖掘技术是在统计学､人工智能(特别是机器学习)和数据库技术等多种技术的基础上发展起来的,强调的是大数据量和算法的可伸缩性｡对于财务人员来说,掌握一些这方面的知识是必要的,不仅可以拓宽现有的知识面,也可以提高自身业务水平,并且可以在实际工作中及时为公司决策者提供更具价值的财务信息｡

主要参考文献

[1] 〔新西兰〕 Ian H Witten,Eibe Frank. 数据挖掘:实用机器学习技术[M]. 原书第2版. 北京:机械工业出版社,2006.

[2] 〔美〕 Michael J A Berry,Gordon S Linoff. 数据挖掘技术:市场营销､销售与客户关系管理领域应用[M]. 原书第2版. 北京:机械工业出版社,2006.

[3] 〔美〕Pang-Ning Tan,Michael Steinbach,Vipin Kumar. 数据挖掘技术导论[M]. 英文版. 北京:人民邮电出版社,2006.

[4] 李剑锋,李一军,等. 数据挖掘在财务分析中的应用[J]. 计算机工程与应用,2005(2):217-219.

[5] 张娴. 数据挖掘技术及其在金融领域的应用[J]. 金融教学与研究,2003(4):15-18.

[6] Robert Groth. Data Mining:Building Competitive Advantage[M]. 2nd ed. NewYork:Prentice Hall PTR,1999.

[7] Xia Hongxia, Shen Qi, HAO Rui. Application of Data Mining Technology to Intrusion Detection System[J]. 通讯和计算机,2005,2(3):29-33.

[8] Chen Bo,Jiang Yongguang,HuBo, LiuJuan. Association Analysis Datamining the Compatibility Regulations of Li Dong Yuan＇s Formula of Spleen and Stomach[J]. 中医药学刊,2004,22(4):613-615.

[9] ZAKI M J,GOUDA K. Fast Vertical Mining Using Diffsets[C]. Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Washington,DC,2003.