实现供货能力承诺的企业高级计划系统研究

曾小青， 刘 宁， 肖海燕

(长沙理工大学 经济与管理学院，湖南 长沙 410076)

自20世纪90年代以来，以制造业为主的中国经济得到了长足发展，中国在全球制造业中比重从3%提高到2007年的13.2%[1]。目前，中国的制造业在全球占有重要地位，位居美国之后，已经成为全球第二大制造业国家。然而，中国制造业生产技术特别是关键技术主要依靠国外的状况仍未从根本上改变。特别是在由美国金融危机引发的全球经济放缓的大背景下，我国制造业的外部需求会有所减弱，这将给我国制造企业带来挑战。但与此同时，“次贷危机”与西方国家经济形势的持续恶化，发达国家的制造业遭受巨大打击，迫于利润与生存的压力，其制造企业将向发国中国家加速转移，从而会促进我国企业的产业结构升级。因此，中国制造业应妥善利用国际国内两个市场，加强产业链上下游企业的协作，在技术、管理和信息化建设方面进行升级，以应对这种严峻又复杂的局面。

一、供货能力承诺(ATP)与高级计划系统(APS)

(一)实现ATP需要强大的计划系统

企业的主要目的是获取利润，而利润来源于产品(或服务)的销售。对制造企业而言，在争取尽可能多的订单的同时，还得按约定交货，履行订单[2]。无论其最终产品具体表现为何种形式，其竞争优势无外乎来自两种能力：一是及时交付产品的能力；二是对整个经营范围内的供货情况进行实时查询的能力，从而向顾客提供最快捷、最准确的信息。这两种能力可归结为企业对供货能力承诺(ATP：Available to Promise)的实现程度。ATP指在整个供应链中对所订购产品进行部件和资源的供货能力核查，基于当前和预定义的计划供给对供货量作出承诺的能力[3]。ATP在供应链的每一阶段，从供应商开始，经过内部设施，直到客户，考虑各类提前期，从而可为客户提供精确的、值得信赖的交货承诺。

实现供货能力承诺的关键是企业要具备强大的生产计划系统[3]。一直以来，企业广泛采用企业资源计划ERP系统对企业运作进行管理，并曾创造了ERP实践的辉煌时期[4]。然而ERP主要是针对企业内部资源的管理，它的核心逻辑基于无限能力假设和固定提前期，缺乏优化功能。同时它不具备协调多个企业资源的能力[5]。为寻求克服ERP的不足，在上个世纪90年代中期，出现了高级计划与排程系统(Advanced Planning and Scheduling，又称高级计划系统或高级计划与排产系统)[6]。APS是一种基于供应链管理和约束理论的先进计划与排程系统，包含了大量数学模型、优化及模拟技术[7～10]。企业对APS系统的需求日渐增长[11]。

(二)APS是ERP计划系统的补充和优化

APS能及时响应客户要求，快速同步计划，提供精确的交货日期，减少在制品与成品库存，并发考虑供应链的所有约束，自动识别潜在瓶颈，提高资源利用率，从而改善企业的管理水平。

但是APS系统不能够独立的运行，它需要大量基础数据的支撑才能良好的运行。一方面，APS的需求计划从ERP的定单输入中获得，然后再结合外部数据中预测需求，通过APS计划模块中的约束条件，得到指导MRP的约束主生产计划，传回到ERP的主生产计划模块。因此，APS不能取代ERP系统，ERP系统采用的计划模型又不能满足目前的需要，ERP的计划模型的改变同时将影响到整个系统结构的变化。因此，用APS来优化ERP生产计划系统，既可以强化ERP的计划功能，同时又不必影响到ERP其他成熟的商业流程。

然而，由于APS的计算复杂性和信息系统的处理能力，目前APS并未得到广泛应用[12]。本文提出了一个实现供货能力承诺的企业高级生产计划模型，并给出求解该模型的启发式算法，并通过在某公司的应用实例验证了该算法的有效性，力图丰富APS的现有研究成果。

二、实现供货能力承诺的企业高级生产计划优化方法

(一)问题的描述及模型建立

对实现供货能力承诺的企业生产计划问题经过简化、提炼后可描述为如下数学问题。

制订生产计划主要考虑关键工序的生产能力。对于关键工序，假设有n批工件p1,p2,…,pn(对应着n个订单)，在某一时间段(计划周期阶段)需经过m台并行设备M1,M2,…Mn加工处理。问如何选择工件加工的批数、每批工件的数量，使得在满足交货期的同时，设备能力与负荷平衡。

对这个问题，可建立如下优化模型：

(1)符号定义：

假设计划周期为K，计划周期中的每个时段为k(k=1,2,…K)；第k时段第j台设备上加工的第i批工件的数量为xijk；tij为第i批工件在第j台设备上的负荷(i=1,2,…n,j=1,2,…m)；第j台设备提供的正常处理能力是NCj，最大能力为MCj；在第k时段第j台设备上工件的转换次数(比如涉及到换模)为CCjk；每次转换的时间为τ；设备在不同批次工件之间转换时，单次转换的损失为α(出于简化，这里假定每次转换时间和损失与具体加工的工件批次无关，大多数情况下这与生产实际是贴近的)；第i批工件交期为Di；第i批工件的单件延期惩罚为βi；计划周期内第i批工件的订单数量为pi，第i批工件是否延期表示为Li，如果不能如期完工，Li为1，否则为0。

(2)优化目标：

求一个工件加工方案(即求每个时段内每台设备加工的工件数xijk)，满足：

(1)工件的延误交货惩罚和转换的损失尽可能小；

(2)在计划周期内，系统中每台设备负荷之差的绝对值总和要尽可能小。

目标函数为：

①按时交货目标：

(1)

②能力平衡目标：

(2)

约束条件为：

(1)每台设备的能力约束：

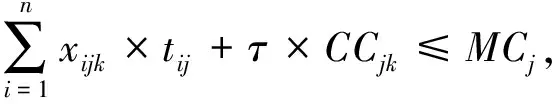
(3)

(2)工件数量约束：

(4)

(3)转换次数：

(5)

(4)第i批工件是否延期：

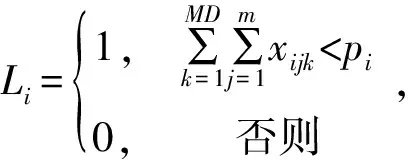
MD=min(K,Di)

(6)

(5)其它约束：

xijk≥0,且xijk∈Z+;tij>0;i=1,…,n;

j=1,…,m;k=1,…,K.

(二)模型求解的启发式算法

上述模型足够简化，且具有较好的普遍性和实用性。作为一个多目标的整数规划模型，可用运筹学软件来求解。然而，它的求解容易受组合优化问题规模的限制，当问题规模很大的时候，求最优解是困难的。因此在实际应用中通常是寻求效率高、优化效果较好的启发式算法。下面给出求解该模型的一种启发式新算法：

通过分析认为，目标①中的式(1)作为第一优先级，目标②的式(2)为次优先级的，因此有启发式规则：先保证交期，再考虑负荷，在满足交期的条件下，尽量均衡负荷；在不能满足交期时，应尽可能将该工件的加工任务安排得靠近Di。

出于算法描述的需要，另外定义几个临时变量：

第j台设备在第k时间段已有负荷为：MLjk，初值为0；

第j台设备在第k时间段的空余能力为：FLjk初值为NCjk；

当前工件尚未安排的加工任务：LT；

Step1 TaskList={p1,p2,…,pn}

Step2i= {i|Di=min(Di0),i0=1,2,…,n}

LT=pi；

forj=1 tom

fork=1 toDi

ifMLjk=0 andLT>0

xijk= min(LT,NCj)

MLjk=MLjk+xijk

FLjk=NCj-MLjk

LT=LT-xijk

ifLT=0 then GOTO Step7

end if

nextk

nextj

end if

Step4 DO

(j,k)= {(j,k) |FLjk=max(FLj0k0),j0=1,2,…,m,k0=1,2,…,Di}

xijk= min(LT,FLjk)

MLjk=MLjk+xijk

FLjk=NCj-MLjk

LT=LT-xijk

ifLT=0 then GOTO Step7

GOTO step3

LOOP

forj=1 tom

fork=1 toDi

xijk=FLjk

MLjk=NCj

FLjk= 0

LT=LT-xijk

nextk

nextj

fork=Di+1 toK

j= {j|FLjk=max(FLj0k),j0=1,2,…,m}

xijk= min(LT,FLjk)

MLjk=MLjk+xijk

FLjk=NCj-MLjk

LT=LT-xijk

ifLT=0 then GOTO Step7

nextk

Step6 MessageBox(“Can not fulfill the order”)

Option=Prompt(“partly arrange or cancel?”,1,2)

if Option=2 then

forj=1 tom

fork=1 toK

MLjk=MLjk-xijk

FLjk=NCj-MLjk

xijk= 0

nextk

nextj

end if

Step7 ifN(TaskList)>0 then GOTO Step2

Step8 End. Each value ofxijkis set.

(三)应用实例

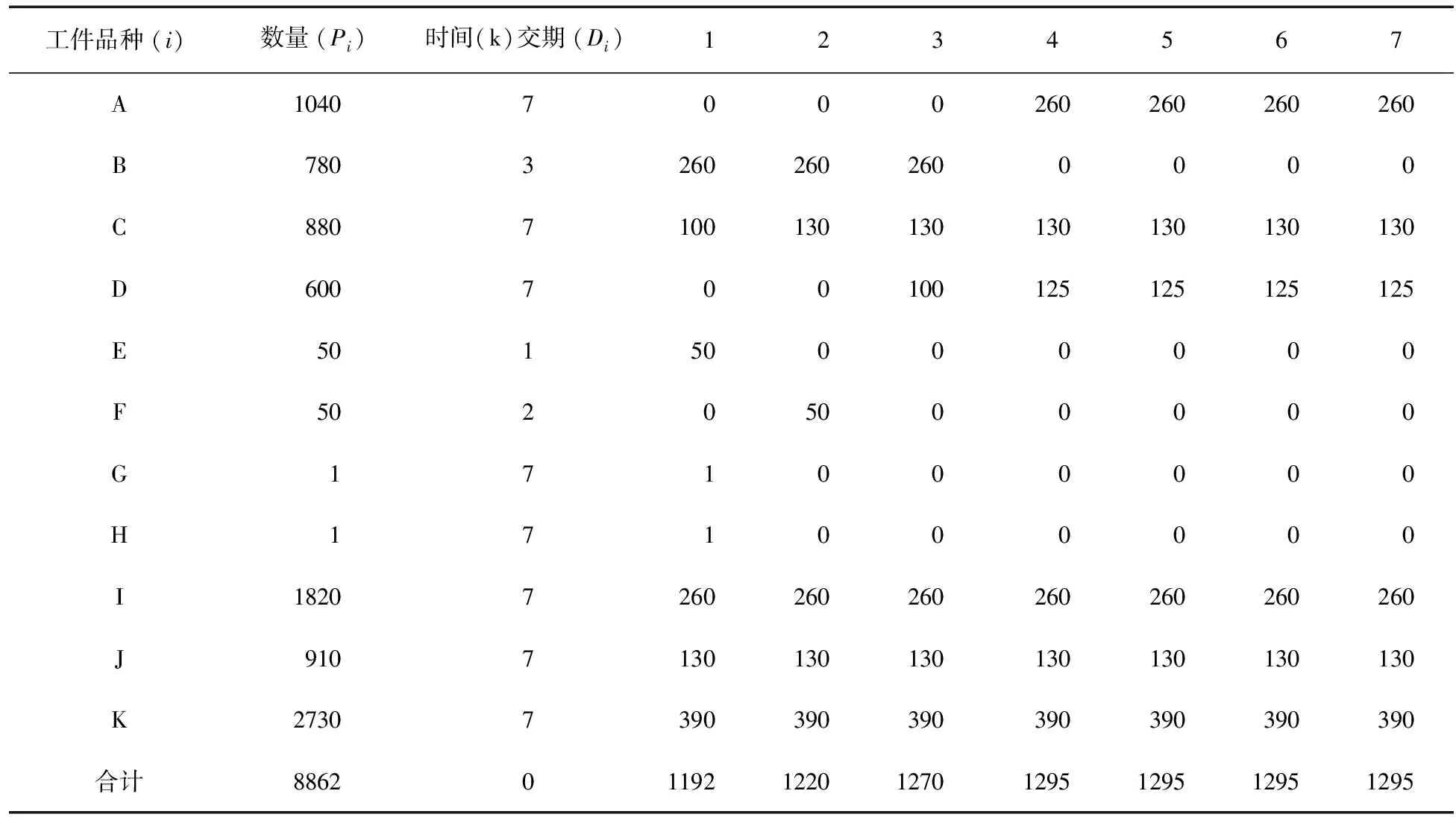
表1 实现供货能力承诺的某企业周生产计划

其它生产线的周生产计划的制定方法类似。图1给出了该企业各生产线的周生产计划计算结果。该企业的生产负荷与生产能力的比较如图2所示。由图2可知，各生产线的生产负荷均未超出其最大能力。生产负荷波动情况这是由每条生产线在该计划周期内的订单数量和交期决定的。从图1中可以看出，a生产线的均衡性比较好(为97.29%)。

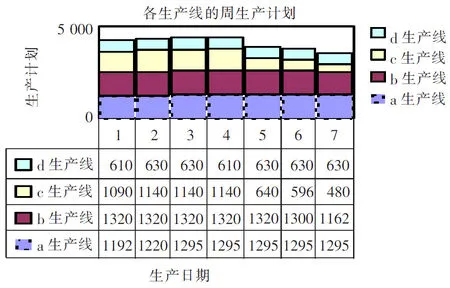
图1 各生产线的周生产计划计算结果

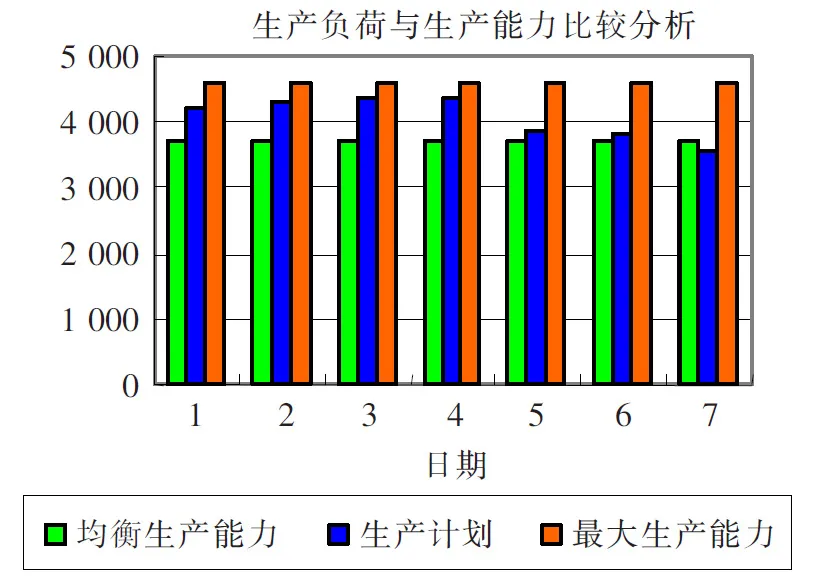
图2 各生产线的生产负荷与生产能力比较

(四)算法分析

(1)计算复杂性

在分析计算复杂性时，只考虑其最高阶的变化，因为这是影响复杂性函数取值大小的主要因素。在该算法中，复杂性主要集中在步骤3和步骤5，其复杂性最大为0(nmk)(为时间多项式算法)。影响步骤3和步骤5复杂性的因素主要有3个：订单批数n，并行设备数m以及计划周期k，此外还受交货期Di的影响。如果交货期Di

(2)算法有效性

此处算法有效性是指计划问题求解过程的有效性，即该过程是否可以保证至少得到一个计划方案。

算法的有效性受订单数量、设备的加工能力以及订单要求的交货期的限制。如果设备的能力充足，并且交货期宽松，则算法能保证获得该计划问题的解。否则，表明不能在该计划周期内完成加工任务，能力不足，计划失败。

三、结论

企业广泛采用企业资源计划ERP系统对企业运作进行管理，高级计划系统APS是ERP的重要补充。而企业制定生产计划的需求信息和资源信息来自多方面，计划的不确定性因素多，要实现供货能力承诺，难度较大，需综合考虑多种约束，综合运用多种优化算法，进行优化求解。本文提出了一个实现供货能力承诺的企业高级生产计划模型，给出了求解该模型的启发式算法，并通过算例验证了该算法的有效性。

[参考文献]

[1]东北证券. 金融危机加速中国制造业格局调整[DB].http://www.nesc.cn/jsp/front/Study/ Index.jsp, 2008-10-30.

[2]Chen,C.Y.,Zhao Z.Y., Ball,M.O. Quanntity and Due Date Quoting Available to Promise[J]. Information Systems Frontiers, 2001,3:477-488.

[3]Bongju Jeong,Seung-Bae Sim,Ho-Sang Jecong et al. An available-to-promise system for TFT LCD manufacturing in supply chain[J]. Computer & Industrial Engineering, 2002,43:191-212.

[4]蔡颖. ERP高级计划APS供应链优化引擎[M]. 广东: 广东经济出版社, 2004.9.

[5]石为人, 余兵. 高级计划排产系统与ERP的集成设计及实现. 重庆大学学报, 2003, 26(11): 87-90.

[6]H. Stadtler, C. Kilger (Eds.), Supply Chain Management and Advanced Planning: Concepts, Models, Software and Case Studies, second ed., Springer, Berlin, 2002.

[7]J.W.M. Bertrand, J.C. Fransoo, Operations Management Research Methodologies using quantitative modeling[J].International Journal of O’perations and Production Management 22 (2), 2002, pp. 241-264.

[8]蓝伯雄. 企业资源优化与优化模型[J]. 计算机集成制造系统-CIMS, 2004, 10 (3):241-251.

[9]Steger-Jensen, Kenn, Hvolby, Hans-Henrik. Analysis of the planning and scheduling functionality in APS systems[C]. Proceedings of SPIE -The International Society for Optical Engineering, 2001, 4566:109-116.

[10]Shin, Kaikou. Feasibility study of real-time scheduling using the Lagrangean relaxation method under an APS environment[J]. JSME International Journal, Series C: Mechanical Systems, Machine Elements and Manufacturing, 2003,46(1):39-45.

[11]Tinham, Brian. APS holds the keys to AWS’manufacturing future[J]. Manufacturing Computer Solutions, 2002,8(3):52-53.

[12]丁斌,陈晓剑. 高级排程计划APS发展综述[J]. 运筹与管理, 2004,13(3):155-159.