台阶坝面消能水气两相流数值模拟
石教豪,韩继斌,姜治兵,李学海
(长江科学院水力学研究所,武汉 430010)
台阶坝面消能水气两相流数值模拟
石教豪,韩继斌,姜治兵,李学海
(长江科学院水力学研究所,武汉 430010)
采用VOF法模拟自由表面,用非结构网格来处理复杂的边界形状,并根据边界形式进行适当的分区,利用k-ε气液两相流模拟光面和台阶溢流面的流场,得到了溢流面的流场、水面线以及消能率等相关水力参数。数值模拟试验结果表明,台阶溢流坝面水流紊动掺气充分,消能率较高,并与物理模型试验结果进行对比分析,二者吻合良好。
台阶消能;水气两相流;VOF法;数值模拟
台阶溢流坝很早就应用于工程,随着碾压混凝土筑坝技术的应用与发展,台阶溢流坝的运用与研究已越来越多地受到广大工程技术人员和学者的关注。国外学者在20世纪80年代以来对台阶溢流坝作了一些研究,而我国学者在90年代以后才对此进行研究。
目前,用数学模型对表孔进行数值模拟的研究成果不多。对表孔进行数值模拟的主要困难在于:表孔水流是无压流,存在着自由水面,涉及到水和气两相,即是二相流问题。汝树勋等在势流假定的基础上,通过迭代自由面残压分布的分析,提出了一种简单、易行的求解带自由面势流问题的方法——残压反馈方法(RPF);陈永明等利用k-ε紊流模型模拟了带有曲线自由表面的阶梯溢流坝和非阶梯溢流坝的紊流流场,采用流体体积分数法(VOF法)来确定自由表面;廖华胜等利用k-ε紊流模型模拟坝面上的复杂紊流流场,对自由水面,引入水-气两相分层流理论中的流体体积分数法(VOF)来迭代求解。二相流问题除了本身理论难度较大外,在进行数值模拟时,对计算机的要求也比较高,且台阶的水体掺气量大,紊动剧烈,较好地模拟台阶坝面二相流一直是计算流体力学的难题。
本课题利用k-ε气液两相流数学模型,采用VOF方法,用非结构网格来处理复杂的边界形状,并根据边界形式进行适当的分区,分别对台阶和光面溢流坝的流场进行了模拟,得到溢流面的流态、流线、水面线等水力要素,分析计算台阶的消能率,并与模型试验结果进行了比较,具体情况详述如下。
1 台阶溢流坝的设计和物理模型试验分析
某水电站枢纽工程采用了碾压混凝土重力坝挡水方式布置,溢流段使用无闸控表孔泄洪,表孔溢流面为WES实用堰型,堰顶高程540 m,堰孔宽度18 m,共3孔,溢流堰总宽59 m(包括闸墩)。堰顶最大设计水头为7 m,定型设计水头为5.25 m,堰顶上游曲线采用椭圆曲线,堰面采用幂曲线接坡比1∶0.85的坝身溢洪道;千年一遇洪水下泄流量275 m3/s,万年一遇洪水下泄流量550 m3/s,可能通过最大洪水下泄流量1 600 m3/s。堰身泄洪采用台阶式溢流面联合下游挑流消能方式,单宽流量3.16~35.59 m3/(s·m)。坝面台阶起始位置设于坝顶曲线段末端,起始台阶高程535.57 m,末级台阶高程413.57 m;根据国内外台阶溢流坝成功案例,台阶高度选用1.0 m,台阶数122。
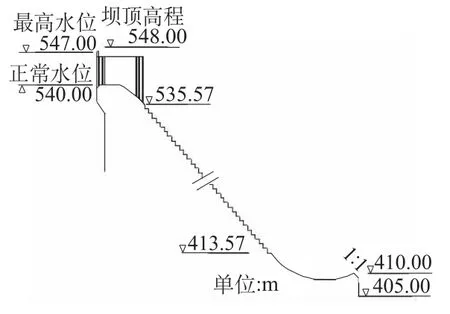
图1 某工程台阶坝面纵剖面图Fig.1 Longitudinal profile of some project stepped dam surface
断面模型试验选用水槽宽度B=0.6 m,上游高度H=2.8 m。模 型几何比尺为Lr=68.33,模拟两孔(含两个整墩),纵剖面布置见图1。
坝面台阶的消能效果一般用消能率来衡量:

式中:E1为以反弧最低点高程为基准面的坝前水流单位水体总能量;E2为反弧最低点水流单位水体总能量。
经过试验,运用公式(1)所得的消能率计算成果见表1、图2。成果表明台阶坝面的消能率随着单宽流量的增大而减小,单宽流量自3.16~35.59 m3/s,相应的消能率达到80%以上,可见台阶的消能作用是相当显著的。
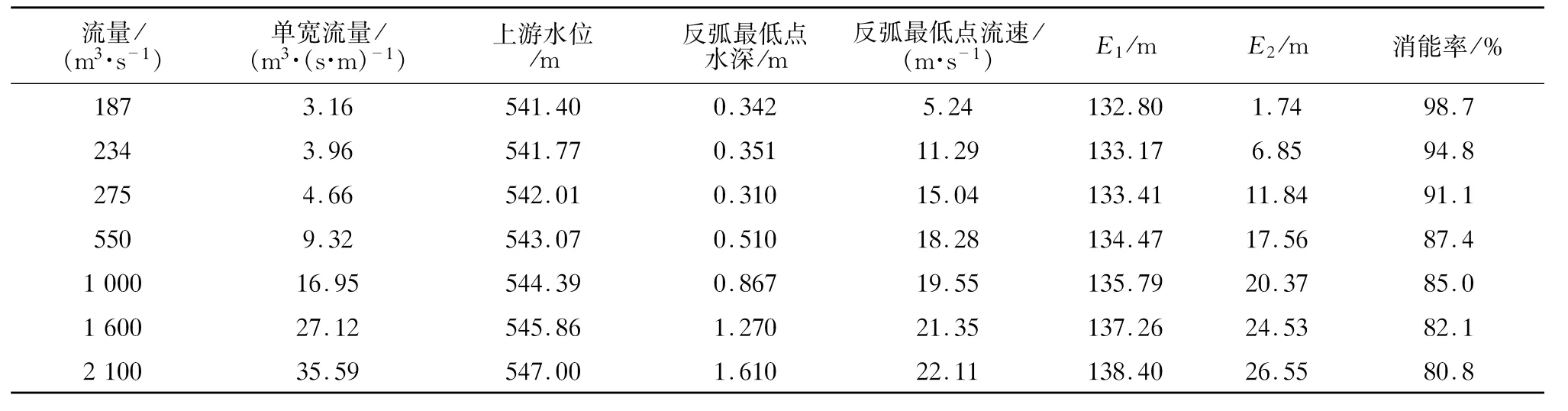
表1 物理模型试验消能率计算成果Table 1 Physical model test results of energy dissipation rate
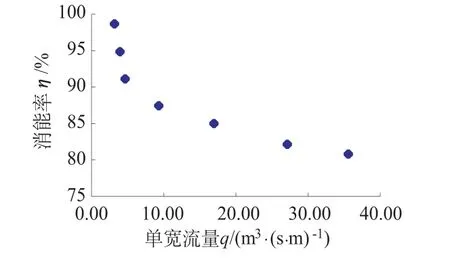
图2 单宽流量与消能率关系Fig.2 The relation of unit width discharge and energy dissipation rate
2 数学模型计算分析
溢流面从上游至下游为等宽,除两侧导墙附近水流三维性较强外,泄槽内水流在垂面上可以概化为二维水流,因此,采用垂面二维数学模型进行模拟计算。
2.1 紊流模型和VOF模型
2.1.1 基本方程
模型的基本控制方程包括连续方程、动量方程、紊动能k方程及紊动能耗散率ε方程。可分别表示如下:
连续方程
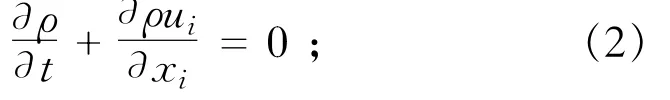
动量方程
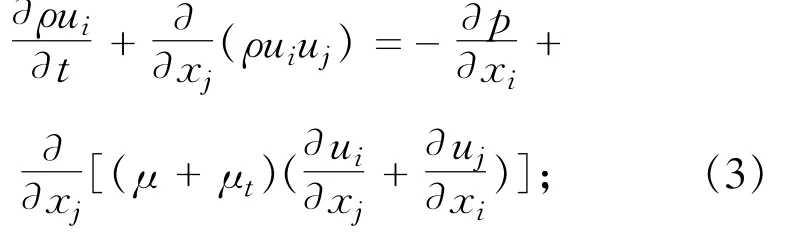
k方程
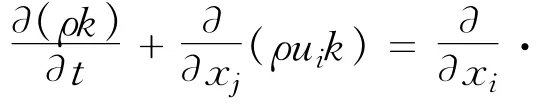
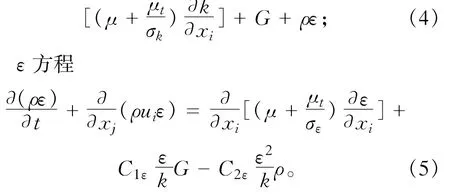
以上各式中:ρ和μ分别为容积分数平均密度和分子黏性系数;p为修正的压力;μt为紊流黏性系数,它可由紊动能 和紊动耗散率 求出,即k ε
2.1.2 模拟自由表面控制方程
引入VOF方法的k-ε紊流模型方程与单相流的k-ε模型形式完全相同,只是密度ρ和μ的具体表达式不同,它们是由容积分数加权平均值给出,即ρ和μ是容积分数的函数,而不是一个常数,其表达式为
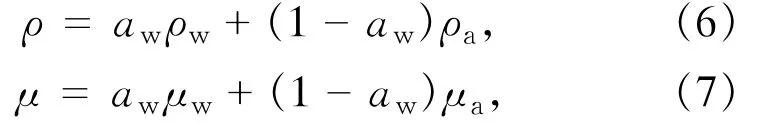
式中:aw为水的容积分数;ρw和ρa分别为水和气的密度;μw和μa分别为水和气的分子黏性系数。通过水的容积分数aw的迭代求解,ρ和μ值都可由上式求出。
水气界面的跟踪即通过求解该连续方程来完成。
2.1.3 求解方法
采用控制容积法求解控制方程,在每个控制容积单元中对微分方程进行积分,再将积分方程线性化,把控制方程离散为可以数值求解的代数方程,就可以得到相应各未知变量,如压力、速度、紊动能及其耗散率ε等变量的代数方程组,然后再对方程组进行求解,就可以求出各未知变量。
自由水面的具体位置采用几何重建格式来确定,采用分段线性近似的方法来表示自由水面线,在每个单元中,水气交界面是具有不变斜率的斜线段,并用此线性分界面形状来计算通过单元面上的流体通量。根据每个单元的容积分数值及其偏微分,线性的水气交界面相对于每个部分充满的单元中心的位置就可以计算出来,从而确定其具体位置。
2.2 计算区域、网格划分以及边界条件
计算区域分为3个部分:库区与堰面段、泄槽段及出口反弧段,其中模拟库区长度36.55 m,大于5倍堰上水头(5H0max=5×7=35 m),沿水深方向33.21 m。光面溢流坝和台阶溢流坝的计算区域分别见图3。模拟工况为表孔堰顶水头547.00,545.86 m,单宽流量35.59,29.66 m3/(s·m)。
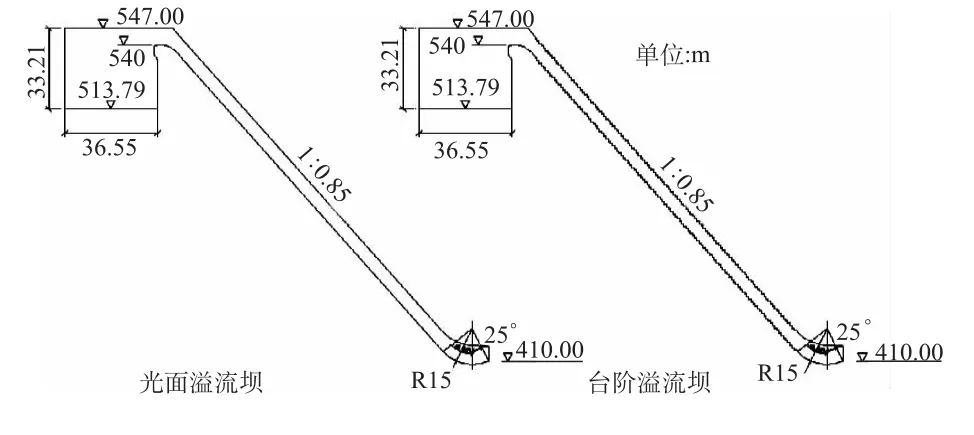
图3 数学模型计算边界条件Fig.3 The boundary conditions of mathematical model calculation
采用三角形网格和矩形网格划分计算区域。光面溢流坝采用三角形网格,见图4;台阶溢流坝库区与堰面及出口反弧段边界形状不规则,采用三角形网格划分,泄槽段采用矩形网格划分,网格分辨率为0.1 m,见图5。

图4 光面溢流坝二维流动计算网格Fig.4 Two-dimensional flow computation grids of a overflow dam with smooth face
进口分为水进口和空气进口2个部分,其中水进口边界设定为速度入口边界。相应的入口紊动能k和耗散率ε的边界条件可由下列经验公式得出:
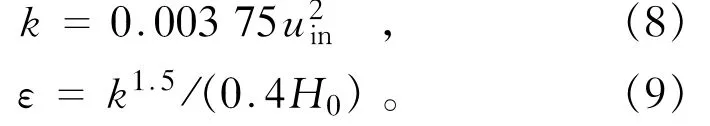

图5 台阶二维流动计算网格Fig.5 Two-dimensional flow computation grids of a stepped overflow dam
2.3 计算结果与分析
以可能通过最大洪水下泄流量1 600 m3/s为例进行计算。
图6和图7分别为光面溢流坝和台阶溢流坝计算得到的流量1 600 m3/s水流运动的水面线和流速分布图。

图6 光面溢流坝流量1 600 m3/s水流运动的水面线和流速分布图Fig.6 Water surface profile in movement and velocity distribution diagram of a overflow dam with smooth surface under discharge being 1 600 m3/s
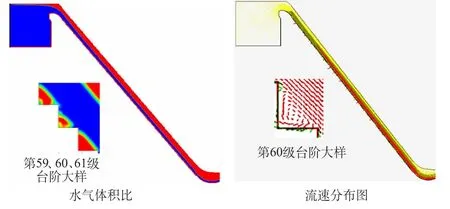
图7 台阶溢流坝流量1 600 m3/s水流运动的水面线和流速分布图Fig.7 Water surface profile in movement and velocity distribution diagram of a stepped overflow dam with discharge being 1 600 m3/s
由光面溢流坝计算结果可以看出,库区水体进入堰面后水面迅速下降,水体势能转化为动能,水流流速增加,水深沿程呈减小趋势;由台阶溢流坝计算结果可以看出,库区水体进入堰面后水面迅速下降,从台阶面起始段至出口反弧段,在台阶溢流坝坝面上可以看到顺时针旋转的漩涡,水体势能转化为动能,水流流速增加,水深沿程呈减小趋势。台阶上游段水深较大,台阶面对自由表面影响较小,因此,水面平滑;台阶中下游段,水深逐渐变小,自由表面受台阶面的影响增大,开始出现波动,越接近台阶面末端,水面波动越大。
水流流过溢流坝面下泄时,由于坝面本身对水流的摩擦作用,总要消耗一部分水流能量;而台阶溢流坝面的台阶的存在增加了坝面的粗糙程度,使得坝面出现许多漩涡,并充分掺气,增强了水流紊动作用,从而提高了坝面的消能效果。在未掺气区,水深流速与光滑坝面相同;进入掺气区后,由于水体中含气量增大,沿程水深减小而流速增大的梯度越来越小,至充分掺气区水深沿程反而增大,流速基本不变。从图7还可以看出:台阶坝面上的速度场可分为两部分,一是较均匀的滑移水流,分布在台阶上侧,二是阶梯内的旋滚水流,分布在台阶内侧,旋滚水流的速度小于滑移水流。在相同水流条件下的同一断面,台阶坝面与光滑坝面比较,水深增大,而流速减小,充分说明了台阶具有良好的消能效果。
消能率计算成果见下表2。成果表明,在流量1 600 m3/s时,光面溢流坝的消能率为32.0%,而台阶溢流坝的消能率达83.8%,可见本工程坝面设台阶后的消能率大大提高,而且掺气充分。计算的台阶溢流坝水面线和流速分布规律基本和物理模型试验结果一致,计算的台阶溢流坝反弧最低点水深为1.338 m,流速为20.27 m/s,模型试验测得的水深为1.27 m,流速为21.35 m/s。从计算结果还可以看出,同流量级的消能率与物理模型成果相当,说明数学模型计算方法是可行合理的。

表2 数值模拟消能率计算成果Table 2 Numerically simulated results of energy dissipation rate
3 结语
通过模拟,得到了光面溢流坝和台阶溢流坝模拟区域的水面线、流速分布及消能率。模拟结果表明:
(1)利用k-ε紊流模型,采用VOF计算方法,较好地模拟了具有自由表面的台阶溢流坝的流场。通过瞬态的迭代求解,水气两相流的VOF模型能够有效地模拟水流的自由表面,计算所得的自由水面与实测值吻合很好。利用非结构网格对计算域进行离散并根据边界形式进行分区,可以克服阶梯溢流坝复杂的边界和几何形状的难题。
(2)从计算结果明显可见台阶坝面出现顺时针漩涡,掺气充分,增强了水流紊动作用。在阶梯坝面上的速度场可分为两部分:一是较均匀的滑移水流;二是阶梯内的旋滚水流,旋滚水流的速度小于滑移水流。
(3)计算流量1 600 m3/s时的光面溢流坝和台阶溢流坝的消能率,分别为32.0%和83.8%,表明台阶的消能率较高,比光面溢流坝的消能率高50%以上,与物理模型试验结果和规律一致。物理模型试验及数学模型计算成果均表明,在本工程所选择的坝面台阶消能是一种非常经济、实用的消能方式,其消能率在80%左右。
(4)自由水面的求解在实际工程中具有重要意义,只要沿溢流坝面的水深己知,台阶的消能率和溢洪道的边墙高度就可以确定。数值模拟比物理模型更省时、更经济,不失为一种很好的研究方法。
[1] 韩占忠,王 敬,兰小平,等.流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2005.
[2] 陆芳春,史 斌,包中进.阶梯式溢流面消能特性研究[J].长江科学院院报,2006,23(1):9-11.
[3] 吴宪生.台阶溢流坝的应用评述[J].四川水力发电,2005,24(1):22-26.
[4] 陈永明,吉庆丰.阶梯溢流坝水流数值模拟及消能分析[J].灌溉排水学报,2006,25(2):68-71.
[5] 潘瑞文,徐一民,杨志林,等.阶梯溢流坝的水流特性与消能效果[J].云南工业大学学报,1995,11(4):1-7.
[6] 廖华胜,汝树勋,吴持恭.阶梯溢流坝流场的数值模拟[J].成都科技大学学报,1995,(5):27-33.
[7] 陈 群,戴光清,刘浩吾.带有曲线自由表面的阶梯溢流坝面流场的数值模拟[J].水利学报,2002,(9):20-26.
[8] STEPHENSON D.Energy Dissipation down Stepped Spillways[J].Water Power and Dam Construction,1991,(9):27-30
Water-Gas Two Phase Flow Numerical Simulation of Stepped Dam Surface Energy Dissipation
SHI Jiao-hao,HAN Ji-bin,JIANG Zhi-bing,LI Xue-hai
(Yangtze River Scientific Research Institute,Wuhan 430010,China)
Using the VOF method to simulate free surface and unstructured grid to deal with complex boundary shape,and conducting the appropriate district based on the border form and utilizing the two phase flow of k-ε water-gas simulating the flow field of the stepped spillway and smooth spillway,the flow field,water surface profile and energy dissipation rate,and other related hydraulic parameters are gotten.The numerical simulation results show that the water flow on the stepped overflow dam face is turbulent with full aeration,the rate of energy dissipation on the steps with choosing a reasonable size is higher,and the physical model test results are analyzed.By comparison,the simulated results are in good agreement with test data,so the two-phase turbulent flow model and the VOF method used for flow simulation on stepped dam face is feasible.
energy dissipation on stepped dam face;water-air two phase flow;VOF method;numerical simulation
TV131.618
A
1001-5485(2009)07-0017-04
2008-07-03
石教豪(1976-),男,湖北大冶人,工程师,硕士,主要从事水工水力学研究,(电话)027-82829903(电子信箱)shijiaohao@126.com。
(编辑:刘运飞)

