论连锁替代

　　说明:本文作于50年代，本文所持论点及所用解析方法，60年代后普遍流行于西方各会计名家的著作乃至工具书中。
　　
　　一
　　
　　连锁替代法在经济活动中的应用甚为广泛，但亦存在一些问题。按照这个方法，在分析计划指标和实际指标间的差异时，必须先假定计划中的某一个因素不变，求得另一个因素变动的影响；之后，在这另一个因素，已经变更，或已被替代的基础上，再假定它这另一因素不变，而求得某一因素变动的影响。
　　假定计划指标为a0b0，实际指标为a1b1，如先假定因素a不变，即：这两个指标以a0b1为诱导数而进行连锁，则a因素的影响为b1（a0- b1），而b因素的影响为a0 (a0- b1)。其具体运算情况如下：
　　
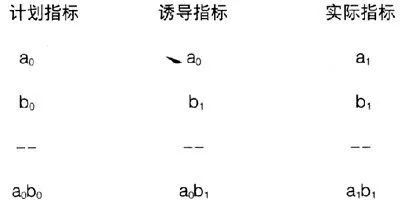
　　a因素变动的影响是：a0b1~ a1b1= b1（a0- b1）
　　b因素变动的影响是：a0b1~ a0b1= a0（b0- b1）
　　反之，如先假定b因素不变，即：这两个指标以a1b0为诱导数而进行连锁则：
　　a因素变动的影响是：a0b0~ a1b0= b0（a0- a1）
　　b因素变动的影响是：a1b0~ a1b1=a1（b0- b1）
　　这就是说，对于同样一个差异，由于替代的顺序不同，或者说，由于所用诱导数的不同，可以得出两个不同的解析，在三个因素下，则可得出四个不同的结果。以a为因素为例，同是(a0- b1)，可以照b1c1计算，也可以照boco计算，可以照b1c0计算，也可以照boc1计算，因素愈多，纷岐愈甚，这是一方面。
　　另一方面，如果a0b1= a1b0(以两个因素为例)，则分析的结果矛盾，试看例1：
　　例1：某单位产品，计划材料成本625元，实际材料成本400元，节约225元，计划单位成本中，用量为100公斤，每公斤计划价格6.25元；实际单位成本中，用量为80公斤，每公斤实际价格为5.00元。如先假定价格不变，即：计划价格和实际用量的积为诱导数而进行分析，则用量差异为：
　　（100公斤-80公斤）×6.25元（计划单价）=125元
　　价格差异为：
　　（6.25元－5.00元）×80公斤（实际用量）=100元
　　两者共计225元，照此分析，材料成本所节约的225元中，125元是由用量的节约而节约的，100元是由价格的减低而节约的。
　　如先假定用量不变，即：实际价格计划用量为诱导数而进行分析，则用量差异为：
　　（100公斤-80公斤）×5.00元（实际单价）=100元
　　而价格差异则为
　　（6.25元-5.00元）×100公斤（计划用量）=125元
　　两者共计亦是225元，但结论却是：材料成本所节约的225元中，125元是由价格的减低而节约的，100元是由用量的减低而节约的，同是100元的节约，按照前一替代顺序是价格上的节约，按照后一替代顺序则是用量上的节约；同是125元的节约，按照前一替代顺序是用量上的节约，按照后一替代顺序则是价格上的节约。替代的顺序不同，不但使分析的结果两歧，而且使分析的结果矛盾。
　　下面这个简单的图可以说明这一点。
　　
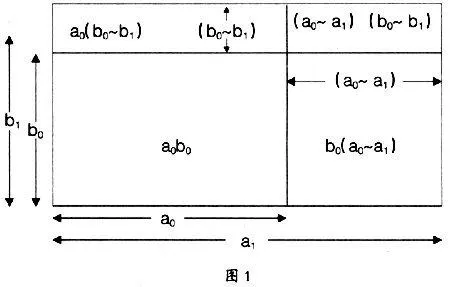
　　这个图中：□a0b0代表计划指标，□a1b1，代表实际指标，计划a0b0变为实际指标a1b1时，其差异如以面积来表示则为□a0b0～□a1b1，这一面积从图上看来可以知道，是由三个面积构成的，即：b0（a0~ a1）;a0（b0~