内含收益率计算方法

　　【摘 要】 本文通过分析内含收益率计算方法的净现值函数及其方程，通过同解变形并利用逐步求导降阶、逐步回溯的办法最终求得符合要求的结果；分析了k的取值域及其对有关函数值的影响，并讨论了多个解的选取问题。
　　【关键词】 财务管理； 内含收益率法； 内含收益率法的解
　　
　　一、内含收益率计算方法
　　
　　在有关资金流量分析等方面，常涉及到应用内含收益率计算方法来计算内含收益率、资金成本率等，那么内含收益率计算方法的取值域怎样？内含收益率计算方法的计算结果是否只有一个解呢？……
　　现假设有已知资金流系列A1、A2、……、An-1、An，要求其内含收益率，除这n个资金流量本身应具有流入流出不同流量方向外（以下不再提该条件），另需满足所有资金流入的现值与所有资金流出的现值相等。即实际上是把这n个资金流按贴现率k换算成现值，如下式所示：
　　g（k）=A1+A2/（1+k）+A3/（1+k）2+……+An-1/（1+k）n-2+An/（1+k）n-1
　　要求内含收益率，即求使得g（k）=0的k，那么，如何来求方程g（k）=0的解呢？
　　
　　二、求解方法
　　
　　可考虑先将该方程进行变换，由于（1+k）≠0，且k>-1，k∈（-1，+∞）（k肯定不能等于-1，一般情况下k也不取小于-1，因为这样会改变各资金流量加项自身的已有正负符号，且有的项变符号，有的项不变符号，与资金流量原有的方向意义不完全相符。当然若其他场合k可以取除-1以外的任何取值，则也可采用本文的求解方法），因此，可在g（k）=0方程的两边同乘（1+k）n-1，得如下式所示的方程f（k）=0，该方程与g（k）=0有同解。
　　f（k）=A1（1+k）n-1+A2（1+k）n-2+……+An-1（1+k）+An=0
　　那么，如何来求出f（k）=0高阶方程的解呢？一种方法是求出k在其取值域内对应的“所有”的f（k）值，并判断是否等于零。这种方法利用计算机求解较方便，但可能运算量较大（经检验，确实如此）。
　　此处讨论另外一种方法——逐步求导降阶法，可考虑对f（k）求一阶导数并令其等于零，目的是求出各极值点，则有下式：
　　f'（k）=（n-1）A1（1+k）n-2+（n-2）A2（1+k）n-3+……+An-1=0
　　要求解f'（k）=0，这又是一个高阶方程，难以求解，是否可以考虑对f'（k）=0再求一阶导数f''（k）并令其等于零，来求出函数f'（k）=0的极值点呢？事实上是可以的，因为f'（k）=0较f（k）=0已降了一阶，而f''（k）=0较f'（k）=0又降了一阶，若逐步这样下去，则会有以下几式：
　　f''（k）=（n-1）（n-2）A1（1+k）n-3+（n-2）（n-3）A2（1+k）n-4
　　+……+An-2=0
　　……
　　f（n-3）（k）=（n-1）（n-2）·……·3·A1（1+k）2+（n-2）（n-3）·……
　　·2·A2（1+k）+A3=0
　　f（n-2）（k）=（n-1）（n-2）·……·3·2·A1（1+k）+（n-2）（n-3）
　　·……·2·1·A2=0
　　方程f（n-2）（k）=0求解的结果是：
　　k0=（n-2）（n-3）·……·2·1·A2/[（n-1）（n-2）·……·3·2·A1]-1
　　若将该结果带入到f（n-3）（k）=0中来考虑求解该方程，则方程
　　f（n-2）（k）=0的解k0将方程f（n-3）（k）=0中k的取值域（-1，+∞）分为两部分，（-1，k0）和[k0，+∞），或（-1，k0]和（k0，+∞）。确定了这两个取值域后，又由于k0点是极值点，因此，函数f（n-3）（k）在两个取值域范围内与横轴最多有两个交点，只要把交点求出来，所求的交点就是f（n-4）（k）的极值点，这样逐步下去，可以最终求解出方程f（k）=0的解，而方程f（k）=0的解就是方程g（k）=0的解。
　　
　　三、实例应用
　　
　　例1：各时刻点有资金流量A1、A2、A3、A4、A5、A6共6个，则可以求出f （4）（k）=0、f （3）（k）=0、f''（k）=0、f'（k）=0、f（k）=0的解如表1所示，那么，f（k）=0的解有3个，且在3个解中，有两个是负值，一个是正值。（表1）
　　
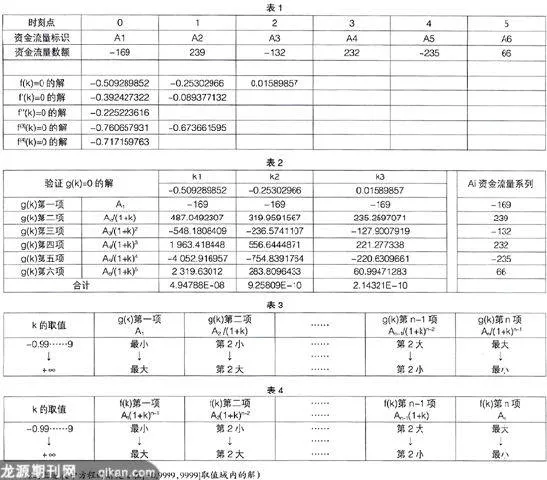
　　表2是验证f（k）=0的三个解k1、k2、k3也是方程g（k）=0的解。
　　
　　四、分析
　　
　　在上例中，如何来理解这三个解呢？是否这三个解都适合六个资金流量的经济意义呢？为了能够更清楚k对g（k）、f（k）的影响，可以将k在其取值域范围内对f（k）、g（k）的影响情况列于如表3、表4。
　　通过表3、表4可知，在k的取值域内，当k∈（-1，0）时，f（k）前面的资金流量被缩小，g（k）后面的资金流量被放大；当k∈（0，+∞）时，f（k）前面的资金流量被放大，g（k）后面的资金流量被缩小。
　　
　　五、结论
　　
　　如何从多个解中选取其中符合实际经济意义的方程的解（k值）呢？这可从k=0时的f（k）、g（k）函数的结果入手来进行分析。特别是，当k=0时，f（0）=g（0）=A1+A2+……+An-1+An，依据该式（称为简单相加）以及上述分析的结果，一般情况下，当正资金流量总量不等于负资金流量总量时（指简单相加），有几种可能情况，一是正（负）的资金流量主要数额在前，负（正）的资金流量相对较小且在后（即两个不同方向主要资金流量数额有明显的前大后小关系），则k应取负值，此时应检查k取负值是否与实际经济意义相符，例如此时可能是亏损等意义，由于后面的资金流量小于前面不同方向的资金流量，因此可通过k取负值的办法使调节后的两个不同方向资金流量数额相等；二是正（负）的资金流量主要数额在后，负（正）的资金流量相对较小且在前（即两个不同方向主要资金流量数额有明显的前小后大关系），则k应取正值，此时应检查k取正值是否与实际经济意义相符，例如此时可能是收益等意义，由于后面的资金流量超过前面不同方向的资金流量的大小，因此可通过k取正值的办法使调节后的两个不同方向资金流量数额相等；三是正（负）的资金流量与负（正）的资金流量间数额大小无一定的规律或规律不明显，此时应综合分析，一方面可以参照前述两种情况所述的判断原则；另一方面，可依据经济意义及无风险收益率等多种情况来综合判断分析。
　　需要指出的是：一般情况下，在f（k）或g（k）中，当|k|越小，所得的f（k）与g（k）的结果受k调节的影响就较小。因此，在所得的几个k值中选取其中之一时，除了考虑k的正负应有其固定的经济意义外，在|k|值的大小问题上，应考虑其影响f（k）、g（k）结果的规律并与无风险收益率等数据进行比较分析。●
　　
　　【参考文献】
　　 [1] 《财务管理》.财政部注册会计师考试委员会.东北财经出版社，1996年3月.