步进电机驱动柔性负载的一种振动抑制控制策略

原劲鹏，刘建功，杨 雷

（北京空间飞行器总体设计部，北京100094）

步进电机驱动柔性负载的一种振动抑制控制策略

原劲鹏，刘建功，杨 雷

（北京空间飞行器总体设计部，北京100094）

针对步进电机的输出力矩特征以及柔性负载的低频振动特性，提出一种抑制柔性负载振动的控制策略。推导了步进电机驱动柔性负载的动力学模型，分析了输入成形法抑制振动的原理并对其进行了扩展，由此产生的步进电机控制逻辑可以有效抑制柔性负载的低频振动。以数据中继卫星的单址天线回扫模式进行了数学仿真，结果表明，提出的控制策略有效且对系统的参数摄动具有一定的鲁棒性。

步进电机；柔性负载；步进逻辑；振动抑制

1 引 言

随着航天技术的发展，挠性化成为越来越多现代航天器的一个重要特点，如航天器带有的大型太阳电池帆板、挠性天线和空间机械臂等。步进电机具有尺寸小、重量轻和功耗小的特点。与其他类型电动机相比它易于开环控制，旋转误差不累积。同时利用步进电机进行驱动，在瞬时断电的情况下具有一定的保持力矩。这些优点使步进电机在卫星工程中被广泛采用。但是步进电机也有其固有的缺陷，即当电机的负载为具有柔性特征的机械结构时，步进电机的步进运动容易激起负载的柔性振动，严重时甚至还会导致负载停转。国际通信卫星V号（Intelsat V）-F2南太阳帆板在轨工作过程中就曾出现过旋转中断几分钟或者停止转动的现象。其主要原因便是太阳帆板的柔性振动与步进电机的振荡相互耦合所致[1]。与步进电机的振荡频率相比，天线、太阳帆板甚至空间机械臂的基频要更低，从能量耗散、任务需求以及系统控制精度、稳定性等方面考虑，对在空间环境下其驱动过程中或驱动结束后的长时间的低频振荡要严格控制。针对该问题，一些学者[2]提出了n-步逻辑驱动控制策略，即当选取步进电机的控制脉冲间隔为某阶柔性模态谐振周期的1/n倍时，作用n步后，由该阶模态引起的柔性振动为零。美国的数据中继卫星即采用这种n-步自动跟踪逻辑，这种方法也是分力合成法的简单应用[3]。该方法的不足之处有3点：1）只有一个振荡频率可被屏蔽；2）鲁棒性较差；3）当步进周期接近某一频率的谐振周期时，有可能激起共振。

针对上述问题，本文将国际上流行的输入成形振动抑制方法用于设计步进电机脉冲逻辑。首先推导了步进电机驱动柔性负载的动力学方程，然后分析了输入成形法振动抑制的原理，针对步进电机的特征对输入成形进行了扩展，由此设计的步进电机驱动脉冲可以避免激起柔性负载的振动，最后对数据中继卫星的单址天线回扫模式进行了数学仿真，验证了所设计算法的有效性。

2 步进电机驱动柔性负载的简化模型

为分析步进电机驱动系统的动态特性，必须建立能够反映系统特性的数学模型。在以往步进电机数学模型的研究过程中，模型结构变化不大，基本上由反映电磁特性的电磁状态方程和反映机械特性的机械状态方程组成。为了突出重点，本文采用中国某卫星帆板驱动方案[4]中使用的步进电机模型，此时其表达式可以写为

式中，Tjmax为最大静转矩，由电机物理结构和绕组匝数等决定；Zr为转子齿数；θc为期望转角或超前角；θ为转子实际转角；T为步进电机输出力矩。

考虑到步进电机的粘滞阻尼，则电机输出力矩为

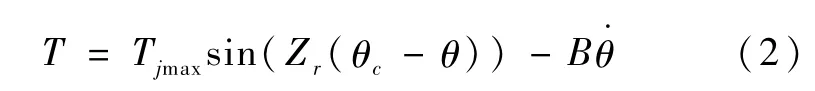
式中B为阻尼系数。

柔性负载单轴动力学方程为

式中，Ia1为柔性负载的单轴转动惯量；ωa1为柔性负载的单轴转动角速度；η1为对应的单轴振动模态；Fa1为柔性负载单轴柔性振动对自身转动的耦合系数；Qa1为柔性负载的单轴驱动力矩，也就是在柔性负载单轴上的步进电机输出转矩；τ1为星体平台对柔性负载单轴的耦合力矩；ξf1为柔性负载单轴柔性振动阻尼系数；ωf1为柔性负载单轴柔性振动模态频率。

根据柔性负载与步进电机的连接模式，设步进电机的转角为θ，柔性负载的单轴转角为θa，谐波齿轮减速器的传动比为N，步进电机转子转动惯量为Js，不考虑效率损失时，有

将式（4）～（6）代入式（3），可得步进电机驱动柔性负载的动力学模型为

3 步进电机驱动柔性负载的控制逻辑设计

3.1 输入成形原理

输入成形是指将由脉冲序列（也称输入成形器）与一定的期望输入相卷积所形成的指令作为系统的输入来控制系统运动。其中，根据系统的刚体运动要求可得到期望输入，保证实现刚体运动；而根据振动系统的频率和阻尼可得到脉冲序列，用于抑制振动。通过求解一定的约束方程组（约束方程可以包括对余振动幅值的约束、对鲁棒性的约束和对成形器时间长度的约束等）可得到脉冲序列中各脉冲的幅值和作用时间。所谓输入成形就是指用脉冲序列将期望的指令形成为新的系统输入。

事实上，输入成形是一种特殊的指令成形技术，其物理实现过程可将输入指令成形简单地视为一个带有若干延迟的1：1增益的新的控制指令，所以一些学者也将输入成形器称为时滞滤波器。其数学模型描述为

式中，Ai为增益，Δt为时间间隔，m为成形器所包含的增益个数，即成形器的容量。根据系统的弱阻尼模态参数，设计合理的Ai和Δt即可达到抑制振动的效果。

由系统的频域理论可知：系统的虚数极点对增益有放大作用，即系统的频率响应在极点处出现谐振。而系统的零点有阻塞对应模态响应的作用，即同样位置处的零点将完全抑制掉该点的增益，重复零点能增强抑制效果。另外，极点附近配置零点（偶极子对）对增益有削弱作用。鉴于成形器只包含零点，如果设计I（s）时，以柔性模态的极点作为其零点，则当成形器作用结束后，系统不会产生相关模态的响应，即残留振动为零。在极点附近配置零点可以减小系统的余留振动。若在系统的极点附近配置多个零点，则设计的成形器对动力学模态参数的摄动具有鲁棒性。几种常用的成形器零点与弱阻尼模态极点的位置关系如图1所示。

图1 理想情况下成形器零点与弱阻尼模态极点的位置关系图

3.2 用扩展的输入成形法设计脉冲逻辑

由步进电机驱动柔性负载的动力学模型可知，要使负载按期望的角度运行，同时尽可能不激励系统中的柔性模态，归根到底要控制作用在负载上的力矩。由于步进电机不能产生任意大小的力矩，只能驱动输出轴使其按某一频率步进，所以无法通过设计传统意义上的脉冲序列来改造步进电机的输出力矩。而参考文献[5]提出用电机的不同数量的高速步进来模拟不同幅值的脉冲力矩，以期对柔性负载产生与输入成形器相近似的影响。具体步骤为：

1）根据柔性负载的模态设计输入成形器，得到一组脉冲序列；

2）将脉冲序列的幅值规范化为电机的步进数，幅值大的脉冲对应一组步进数多的执行步，反之则相反，所有的步进运动均以电机的最高速率运行；

3）每一组步进的起始时间设为原始的脉冲产生时间；

4）根据每组电机步进运动所需时间，适当调整每组步进的开始时间，使每组步进运动的中心尽量接近原始的脉冲产生时刻。

扩展的输入成形法的示意图如图2所示，最上面的图代表一台四脉冲成形器，中间的图代表多组成形器的步进运动，每组成形器步进的步数与对应时刻脉冲的幅值成正比，最后要对起始时间进行微调。

图2 扩展的输入成形法的示意图

由于单个脉冲对应的步进数往往不是整数，所以必须进行取整运算以产生步进电机的脉冲指令。为了最大程度地逼近输入成形器对柔性结构产生的影响，需要对取整运算的误差进行约束。取整运算产生的全部误差定义为

式中，2N+1为脉冲序列的容量，ai为第i个脉冲应该分配的步进数，round（*）表示向下取整。

单个脉冲转化时产生的最大误差为

式（9）和式（10）分别用来选择规范整个成形器对应的步进数和单个脉冲对应的步进数。考虑到理想脉冲幅值与取整后步进电机的步进数不同，必须使柔性结构敏感确切的步进数，否则就不能达到抑制振动的效果。

4 算例分析

下面通过算例说明该方法的有效性。以数据中继卫星的单址天线[6]为柔性负载模型进行数学仿真。为简单起见，这里只给出针对一阶模态所设计的脉冲逻辑的仿真结果。成形器对于多模态的振动抑制可参考文献[7]。以步距为1.5°的三相扇形永磁步进电机为对象，谐波齿轮减速比为1/200，步进电机参数如表1所示。

表1 步进电机参数

表1中J即式中的Jh，表示折算到电机轴的转动惯量，步进电机控制脉冲的最小死区时间为0.005s。

针对天线的基频，设计四脉冲成形器为

以天线回扫模式对仿真情况进行说明。设天线需要转动0.06°，即电机步进8步。规范化的步进电机的步进序列为

采用8-步步进逻辑和式（12）给出的步进逻辑时，天线的振动模态坐标如图3和图4所示。由仿真结果可以看出：当天线的模态频率取标称值时，8-步步进逻辑能够得到完美的死区响应，抑制振动的效果优于扩展的输入成形法（后者不可避免地带来取整误差），但当频率变化到20%时，基本上已经失去振荡抑制效果，而后者具有较好的鲁棒性。事实上，这时2-步步进逻辑便相当于ZV型成形器。

假设天线需要转动0.225°，则步进电机需转动30步，将其规范化为步进电机的步进序列，则

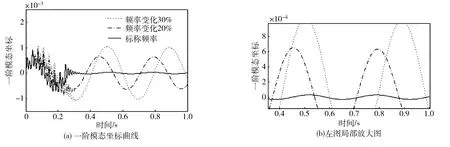
图3 采用8-步步进逻辑时的仿真结果

图4 采用扩展输入成形法生成步进逻辑时的仿真结果

采用式（13）给出的逻辑驱动天线，其仿真结果如图5所示。在同样的时间内以电机匀速步进30步的方式驱动天线，其仿真结果图6所示。从仿真结果可以看出，当不采取减振措施时，电机会出现失步。这也从另一个角度说明了本文方法的有效性。

图5 采用扩展的输入成形法使天线转动0.225°时的仿真结果

图6 常速率驱动使天线转动0.225°时的仿真结果

5 结 论

针对步进电机的输出力矩特征以及柔性负载的低频振动特性，提出了扩展的输入成形技术，即将脉冲序列用步进电机的步进运动进行等效，使步进结束后负载的振动为零或将余振动控制在一定范围内。步进运动的每一组步进数都由脉冲序列中所对应时刻的脉冲幅值决定，步进运动的间隔则由脉冲时间确定。该方法能够有效地削减由步进电机步进运动引发的柔性负载的低频振荡，防止天线框架驱动机构的失步与堵转，并能具有一定的鲁棒性。

[1] 刘暾.一个值得注意的现象——挠性附件驱动系统的堵转现象[C].全国第七届空间及运动体控制技术学术会议，西安，1995

[2] Schmeichel H，McElroy T T.TDRSS single-access control system[R].AAS-007，1980

[3] 王凤鸣，陕晋军，高桦，等.应用分力合成方法的步进电动机驱动方案研究[J].上海航天，2001，18（3）：8-14

[4] 王凤鸣.太阳帆板驱动系统堵转现象的理论分析及实验研究[D].哈尔滨工业大学博士学位论文，2001

[5] Doherty JM，Tolson H R.Input shaping to reduce solar array structural vibrations[R].NASA/CR-1998-208698，1998

[6] 佘海鹰，曲广吉.中继卫星正常模式星体和天线两级控制耦合动力学初步仿真[C].全国第八届空间及运动体控制技术学术会议，黄山，1996

[7] Yuan，JP，Yang D，Wei H T.Flexible satellite attitude maneuver control using pulse-width pulse-frequency modulated input shaper[C].The 1stInternational Symposium on Systems and Control in Aerospace and Astronautics，Harbin，China，January 19-21，2006

A Vibration Suppression Control Strategy for Step Motor Driving Flexible Payload

YUAN Jinpeng，LIU Jiangong，YANG Lei
（Beijing Institute of Spacecraft System Engineering，Beijing 100094，China）

Considering nonlinearity of step motor's output torques and low frequency vibration characteristics of flexible payload，a method for designing control command of step motor is proposed to suppress the residual vibration in this paper.The dynamics model of step motor driving flexible load is derived，indicating proper step logic design is a feasible solution of vibration suppression.Furthermore，as a feed forward control strategy of vibration suppression，the input shaping technique is analyzed and its modification for flexible payload driven by step motor is put forward.Simulation results validate that this method can be used to generate step logic for single access antenna slew mode.

step motor；flexible payload；step logic；vibration suppression

TM383.6

A

1674-1579（2008）06-0034-05

2008-05-01

原劲鹏（1978-），男，山西人，博士，研究方向为航天器动力学与控制（e-mail：hit_yuan@sina.com）。