高速单体船航行性能综合优化的遗传混沌算法

1 引 言

船舶是一种可在水面或水中移动的建筑物，它具有技术复杂、投资大和使用周期长的特点，并与国民经济和国防建设等许多方面有着非常密切的关系。船舶设计是一门多学科高度综合的科学技术，其过程一般认为是“在满足特定任务要求的前提(或条件)下，初步拟出若干可行方案，并对这些可行方案进行单项或综合分析，且按照一定的准则进行评估，筛选出少量设计质量较高的方案，再进一步对其参数尺度优化”的过程。这一过程涉及经验知识、基础或专业理论知识，是一个多因素和多约束条件(相关性联系)综合权衡、逐步逼近的过程。然而，各因素及其相关性联系间通常又是一个多分枝的复杂网络关系，要达到预期的目的显然路径不是惟一的。在这一过程中，船舶动力学性能优劣与船型参数相关分析是一项非常重要的工作，单个性能的优劣评判与船型参数相关性的描述多数能采用理论分析或试验手段解决，但这远远不能满足现代船舶设计的要求。随着计算机科学技术的迅速发展和数学规划理论的不断完善，优化技术在各个工程领域中的应用日益广泛。众所周知，常规优化方法如单纯形法等常常陷入局部最优而不能自拔，采用具有较强全局寻优能力的遗传算法能有效地克服这一缺陷，但是对于船舶性能综合优化这类非常复杂的多目标、多约束和多变量工程优化设计问题，优化计算耗时较长，同时优化计算过程中早熟现象出现的概率较高。本文尝试将遗传算法与混沌算法复合应用于高速单体船航行性能综合优化计算中。

2 遗传混沌算法及其优化计算

2.1 优化方法

遗传算法(Genetic Algorithms,简称GA)[1]是人工智能的重要新分支,是基于达尔文进化论,在计算机上模拟生命进化机制而发展起来的一门新学科,是一种广为应用的、高效的随机搜索与优化的方法。它根据适者生存，优胜劣汰等自然进化规则来进行搜索计算和问题求解。与传统的优化方法相比较，它具有使用简单、不依赖于问题的数学特征、全局寻优能力强等特点，因此，遗传算法是一种理想且高效的搜索(或优化)方法。考虑到遗传算法面对船舶航行性能综合优化这类非常复杂的多目标、多约束和多变量工程优化设计问题，带来的特大种群规模和特别复杂的适应度函数处理及计算时间过长和较大概率的早熟问题，本文采用的优化计算分两步走：首先，采用遗传算法进行有限代数计算，并在遗传算法程序中嵌入辅助进化子函数，从每次计算后的种群中选择4个适应度相对较高的个体进行混沌搜索。接着，在遗传算法优化结果的小范围内采用二次载波混沌算法进一步完成最优值点的计算，作为改进后的遗传混沌算法，具体实现细节见下文。

2.1.1遗传算法优化

遗传算法求解[2]的组成为:

1) 编码方法

在遗传算法中对每一个染色体进行适当的编码是必不可少的一步，算法中问题的构成以及遗传算子的使用都取决于编码方式。这些编码方法可以分为三大类：二进制编码方法、浮点数编码方法和符号编码方法Holland的简单遗传算法采用的是二进制编码，二进制编码理论分析方便，遗传操作与生物进化相似，能在相同的范围内表示最多的模式，能够充分体现隐性的并行性。

2) 选择

选择是实现进化的重要一环，许多学者提出了种种不同的选择方法，这里采用比较通用的轮盘赌法。

3) 交叉

交叉运算使用单点交叉算子。在生物的自然进化过程中，两个同源染色体通过交配而重组，形成新的染色体，从而产生出新的个体或物种，在遗传算法中也使用交叉算子来产生新的个体。单点交叉算子是最常用和最基本的交叉操作算子。

4) 变异

在生物的遗传和自然进化过程中，其细胞复制环节有可能会因为某些偶然因素的影响而产生一些复制差错，这样会导致生物的某些基因发生某些变异，从而产生新的染色体，表现出新的生物性状。在遗传算法中也引入了变异算子来产生新的个体。基本位变异算子是最简单和最基本的变异操作算子。对于基本遗传算法中用二进制编码符号串所表示的个体，若需要进行变异操作的某一基因座上的原有基因值为0，则变异操作将该基因值变为1；反之亦然。

5) 适应度值

在遗传算法中，适值是一个至关重要的概念。对于无约束优化问题，适值可取为该问题的优化目标值。但对于有约束的优化问题，适值就不一定是该问题的优化目标值。但其对应关系应是明显的。实际上，正是通过适值的合适选取，可将约束优化问题转化成无约束优化问题。我们知道，约束优化问题的一个可行解应满足约束条件，而最优解不但要满足约束条件，还必须使得目标函数值最大或最小。

6) 进化停机准则

如果对遗传算法的搜索过程进行跟踪观察，我们会发现它将很快收敛于一个稳定的最优解。在实际优化过程中，为提高计算速度，可每隔10代判断一下迭代是否收敛，方法是计算出这代个体的适值的方差，当它小于给定的值εs：(可取为1.0e-5)时，即认为找到最优解，可提前停止搜索。

7) 惩罚策略

惩罚技术大概是用遗传算法解约束优化问题中最常用的技术。本质上它是通过惩罚不可行解将约束问题转化为无约束问题。在遗传算法中，惩罚技术用来在每代的种群中保持部分不可行解，使遗传算法可以从可行域和不可行域两边来达到最优解。惩罚策略[3]的主要问题是如何设计一个惩罚函数，从而能有效地引导遗传搜索达到解空间的最好区域。

2.1.2混沌算法优化

混沌算法求解的步骤为:

本文的混沌算法优化[4]采用二次载波混沌算法。混沌优化是通过混沌变量实现的。混沌变量的产生有多种方法。这里选用应用较为广泛的Logistic映射，其方程如下：

zk+1=μzk(1-zk)

(1)

式中,μ是控制参数。不难证明，当μ=4时，式(1)完全处于混沌状态，在数学上的解释就是通过式(1)的迭代可“随机”产生(遍历)(0，1)之间除去不动点(即0.25，0.5，0.75)之外的所有数值。利用混沌对初值敏感的特性，赋予式(1)n个(0，1)之间的不同的初值(不动点除外)，即可得到n个轨迹不同的混沌变量。基于二次载波的混沌优化基本步骤为：

1) 初始化。k=0(k为首次载波迭代步数)，给予式(1)n个不同的初值zi,0。(初始设计变量)，得到n个轨迹不同的混沌变量zi,k+1；

2) 通过下式进行首次载波：

xi,k+1=ci+dizi,k+1

(2)

式中，ci和di为常数，相当于平移和放大参数，其目的是将选定的n个混沌变量“映射”到优化变量中。显然，ci=ai，di=(bi-ai)，ai和bi分别为设计变量的下限与上限；如果自变量取值范围是开区间，则ci=ai-εci，di=bi-ai-εdi，其中εci和εdi为很小的正数，可取为10-10，且εci<εdi；

3) 进行首次载波后的迭代搜索。先令Xk表示xi,k(i=1，2，…，n)，相应的性能指标为fk，当前最优值点为X*，最优值为f*，并且X*(0)=X0，f*(0)=f0；

4) 若经过3)若干次的搜索，f*都保持不变，则按下式进行二次载波：

(3)

式中，k′为二次载波后迭代步数，初始为0，aizi,k′+1为遍历区间很小的混沌变量，ai为调节常数；

5) 用二次载波后的混沌变量继续迭代搜索，过程类似步骤 3)；

6) 如果满足终止条件，则输出最优解X*及最优值f*，否则返回步骤5)。

3 航行性能综合优化计算的数学模型

本文将快速性、耐波性和操纵性三项性能指标加权作为优化目标函数，而将稳性和浮性等其他一些性能及其船型主要要素(参数)的限制作为优化约束条件，构成一种高速单体船性能综合优化计算的数学模型[5]，具体描述见下文。

3.1 设计变量

高速单体船航行性能综合最优可能性分布函数的计算问题较为复杂[6]，涉及的船型参数也很多。经综合分析现选择以下14个参数作为设计变量：船长L，船宽B，吃水T，纵向棱形系数Cp，舯横剖面系数Cm，设计水线面系数CW，浮心纵向位置LCB(%LPP)，螺旋桨直径DP，盘面比AE/A0，螺距比P/DP，螺旋桨转速n，设计航速Vs，半进水角ie，尾板相对浸湿面积At/Am等参数。通常将它们定为设计变量，可采用下列向量形式表示为：

3.2 目标函数[7]

选取海军系数的倒数作为快速性指标

(4)

式中，Δ为排水量；PE为有效功率；η0为螺旋桨敞水效率；ηH为船身效率；ηR为相对旋转效率；Rt为总阻力，可以根据经验阻力系数回归公式得到[8]。

操纵性的评判涉及到许多方面，这里为使问题不过于复杂，选取直线稳定性指数VarL与回转性指数VarT，两者的线性加权平均和MV=aVarL+bVarT(a、b分别为两个操纵性能的权重，本文对a、b的取值分别为0.7和0.3)。和CSP一样，Mv也是设计变量X的函数，记为MV=MV(X)。

对于耐波性，可取船舶在波浪中的纵摇角度和升沉幅值经压缩至0～1之间的加权平均为目标值，记目标值为Sv，它是关于设计变量X和风、流、浪等环境参数的函数，现指定海况，则可记SV=SV(X)。本文对耐波性两个权值的取值为0.5和0.5。

对上述三个指标，可取它们压缩至0～1之间的线性加权平均值为动力学的目标函数。此时目标函数为：

f(X)=α1CSP01+α2MV01+α3SV01

(5)

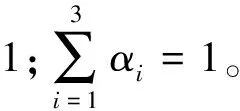
3.3 约束条件

3.3.1等式约束[9]

等式约束包括满足浮性条件，Δ=LBTCB；螺旋桨的有效推力与船舶航行时遭受的阻力相等；设计状态下主机供给螺旋桨的转矩必须等于螺旋桨吸收的转矩。

3.3.2不等式约束

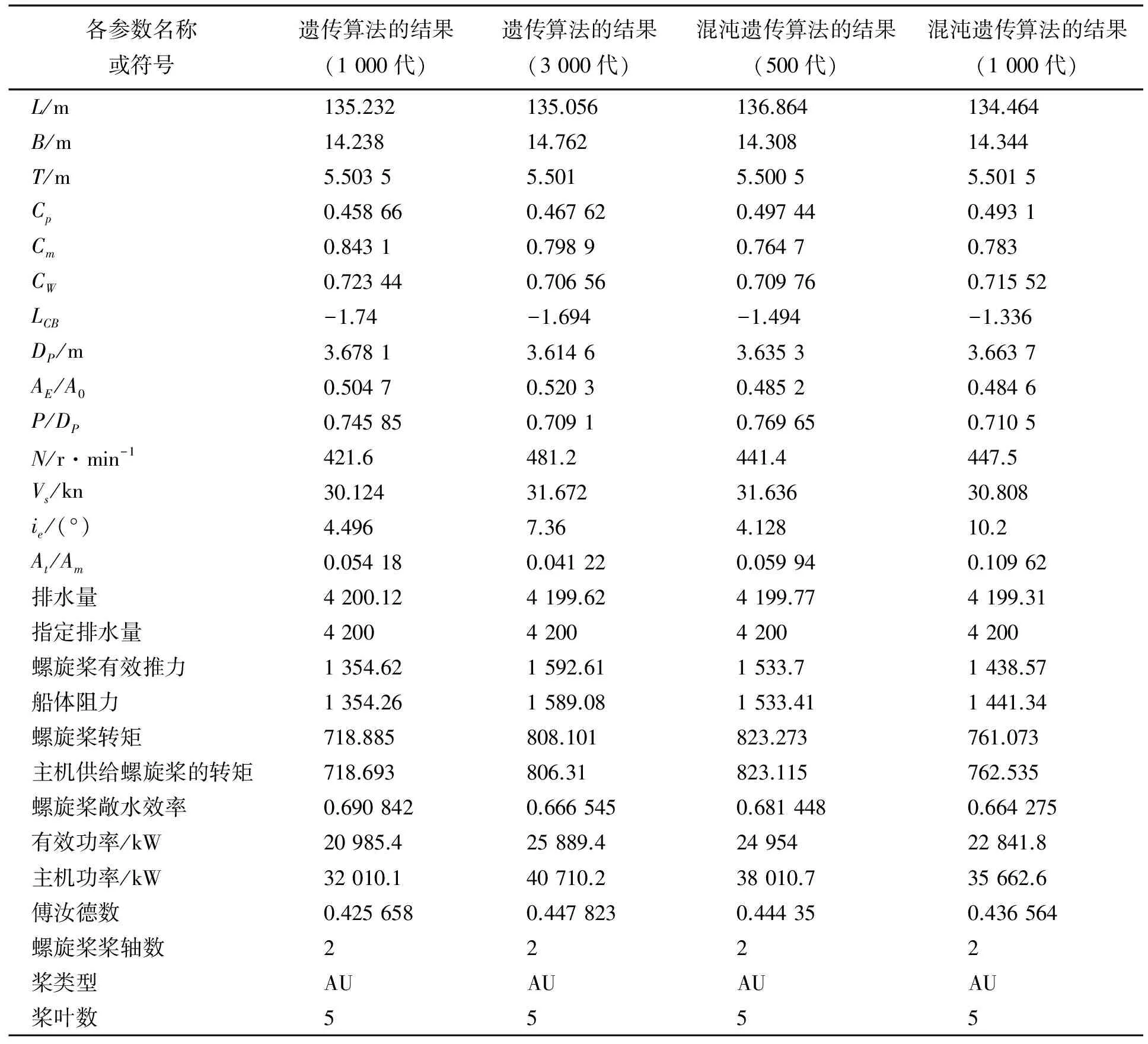
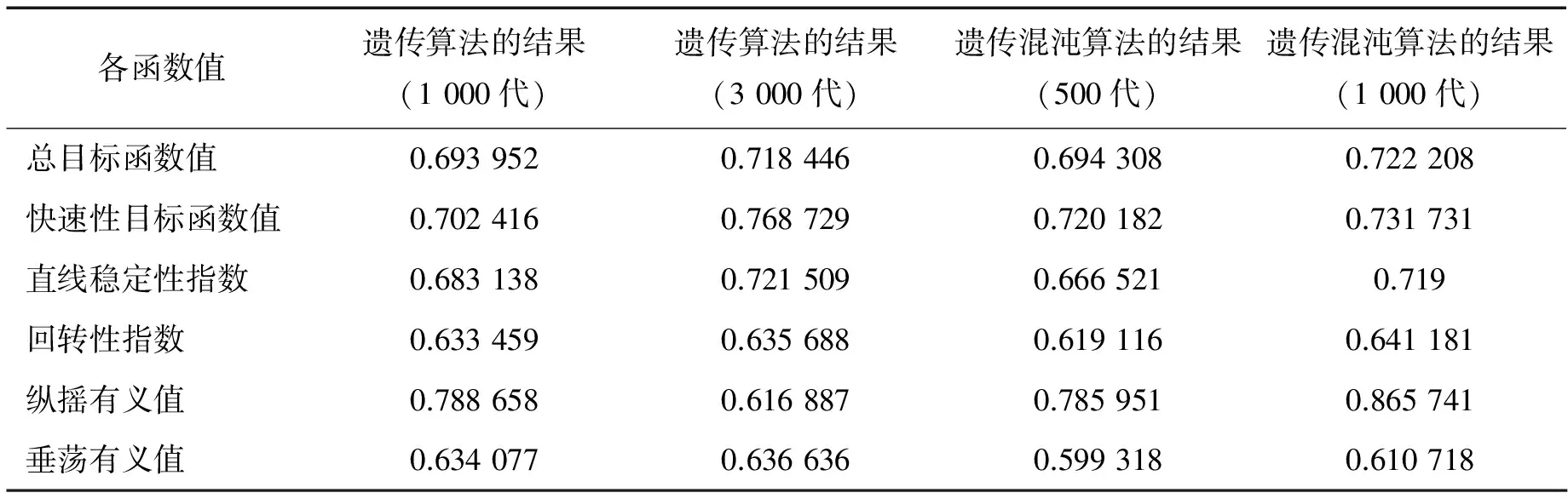
不等式约束包括14个设计变量取值范围； 初稳性高度条件：初稳性高GM>a；极限横摇幅值衡准条件：Φa≤b；回转性衡准条件：相对回转直径Ds

4 优化计算及结果分析

4.1 优化计算

船舶航行性能综合优化计算问题至少涉及到14个设计变量，包括3个等式约束和5个不等式约束，若记入变量上下限约束，则不等式约束将多达30个。显然，这是一个非常复杂的工程优化问题。本文采用如上所述的遗传算法与改进的遗传混沌算法和上述数学模型编制了计算软件。限于篇幅，在此仅以排水量为4 200 t的高速单体船为计算和比较分析实例。该船优化设计变量范围列于表1。

表1 设计变量范围

表2 各变量及参数的计算结果

表3 各目标函数的计算结果

4.2 优化结果分析

由表3显然可见，3个等式约束的满足程度高达99.9%以上。同时，不等式约束均获得100%的满足，说明优化方法计算精度高。其它结论或建议如下：

1) 基于多目标综合优化数学模型，遗传算法进行了1 000代的优化计算，而其总目标函数值为0.718 446，较基于3 000代遗传算法优化计算的目标函数值0.694 308低约3.41%，呈现出明显的早熟特征；基于一次载波1 000次及二次载波1 000次的遗传混沌算法优化计算(500代)的总目标函数值为0.694 308，较基于一次载波1 000次及二次载波1 000次的遗传混沌算法优化计算(1 000代)的总目标函数值为0.722 208低约3.86%，可见遗传混沌算法对于单纯的遗传算法明显占优势；

2) 借助多目标综合优化数学模型，基于遗传混沌算法的优化计算的目标函数值在1 000代左右趋于稳定，2 000代时的数值为0.722 762，与1 000代的数值相差0.077%。本文对遗传混沌算法的计算代数为1 000代时的数据进行分析。对于6 000代遗传算法的优化计算得出总目标函数值为0.720 03(耗时10′56″)，相对基于一次载波1 000次及二次载波1 000次的遗传混沌算法优化计算(1 000代)的总目标函数值为0.722 208(耗时8′50″)。由此可见，上述遗传混沌算法可以非常有效地提高求解复杂三多(多目标、多约束和多变量)工程优化问题的计算效率。

对于船舶整个使用寿命上来说，其累计经济损失还是不可忽视的，优化计算的作用更为突出了。

5 结 论

综上所述，本文提出了一种改进的遗传混沌算法，应用于高速单体船航行性能综合优化计算的结果表明：该算法不但能有效地克服遗传算法的早熟问题，而且计算代数少、效率高。为有效解决复杂的多目标、多约束和多变量工程优化设计问题提供了一种行之有效的途径。根据大量优化计算表明：该软件运行稳定可靠，为船舶设计方案的综合评估及船舶参数的综合决策准备了条件。同时，顾及具体船型及其航行环境条件，特别是对包含结构静力学和动力学特性解析描述的综合优化数学模型研究是很有价值的。

[1] 王健，王建华.标准遗传算法的研究进展[J].华东船舶工业学院学报,2000,(3):28-34.

[2] 米凯利维茨．演化程序一遗传算法与数据编码的结合[M]．北京：科学出版社,2000.

[3] 张火明，杨松林．遗传算法在船舶航行性能优化中的惩罚策略[J]．华东船舶工业学院学报，2001(4):2-4.

[4] 李吴，胡云昌，曹宏铎．加速混沌优化方法及其应用[J].系统工程学报，2002,(1):41-44.

[5] YANG S L，CHEN S L,ZHU R Q, et al. Determination of hull form parameters of large-scale ship based on synthesis optimization of ship navigation performance[J].Journal of Ship Mechanics,2005,9(6)：31-38.

[6] 杨松林,朱仁庆,王志东,张火明.大型中速船舶快速性和操纵性综合优化研究[J]．船舶,2003(5):18-23.

[7] 杨松林，奚炜，张火明. 吃水受限的内河大型船舶航行性能综合优化方法研究[J].船海工程.2006,(1):8-11.

[8] 朱珉虎(译).高速方艉船型功率预报方法——基于速度的再回归[J].中外船舶科技，2004(4):33-42.

[9] ZHANG H M，Yang S L．The penalty strategy of genetic algorithm is ship navigation performance optimization[J]．Transaction of East China Shipbuilding Institute，2001(4):13-19.