龙门起重机结构模态分析

武汉理工大学 物流工程学院 武汉 430063

在龙门起重机结构的设计过程中一般首先考虑的是结构的静强度和刚度，难免会使局部结构不合理。龙门起重机结构振动特性的优劣对整个龙门起重机的性能有重要的影响。振动不但可能造成龙门起重机结构的疲劳破坏，还会产生共振和噪声。当所受激振力的频率与龙门起重机结构的某一固有频率接近时，就有可能引起结构共振，从而产生很高的动应力，造成结构的强度破坏或产生不允许的大变形，破坏龙门起重机的性能[1]。因此，具有足够的刚度是龙门起重机设计的基本要求，必须对龙门起重机结构进行模态分析。

1 模态分析基本理论

对具有有限个自由度的弹性系统运动方程，可应用动载荷虚功原理推导，其矩阵形式为[2]

[M]{δ}+[C]{δ}+[K]{δ}={P}

(1)

式中:[M]—结构总质量矩阵；

[C]—结构总阻尼矩阵；

[K]—结构总刚度矩阵；

[δ] —节点位移列阵；

{P}—结构载荷列阵。

在模态分析过程中，取{P}为零矩阵，因结构阻尼较小，对结构的固有频率和振型影响甚微，可忽略不计，由此可得结构的无阻尼自由振动方程

[M]{δ}+[K]{δ}={P}

(2)

这是常系数线性齐次微分方程组，其解的形式为：

{δ}={δ0}sin(ωt+φ)

(3)

式中:ω——振动固有频率；

φ——振动初相位。

将(3)式代入(2)式后，便得到：

{[K]-ω2[M]{δ}}=0

(4)

式(4)有非零解的条件是其系数行列式等于零，即

|[K]-ω2[M]|=0

(5)

当矩阵[K]以及[M]的阶数为n时，式(5)是ω2的n次实系数方程，称为常系数线性齐次常微分方程组(2)的特殊方程，系统自由振动特性(固有频率和振型)的求解问题就是求矩阵特征值ω和特征向量{δ}的问题。

2 龙门起重机模型

以JMQ50型龙门起重机为例，整个龙门起重机的结构组成见图1。

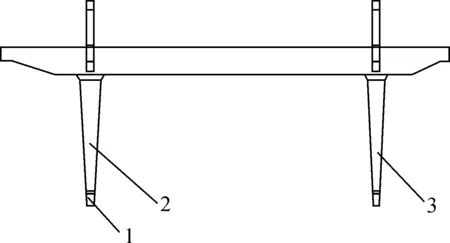
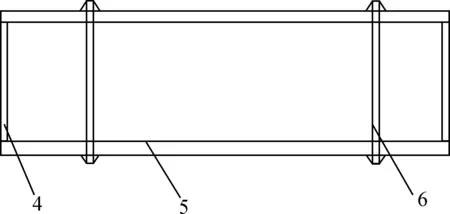
1-下横梁；2-刚性支腿；3-柔性支腿；4-端梁；5-主梁；6-门框结构。图1 JMQ50龙门起重机结构

龙门起重机的基本设计参数如下：

额定起重量50 t 起升高度16.5 m

跨度45 m 有效悬臂长度11.15 m

工作级别：A7 额定起升速度18 m/min

小车运行速度：75 m/min

利用shell63单元对龙门起重机整机进行建模。该龙门起重机结构大部分是由Q235钢板焊接的，某些局部地方用Q345钢板加强，在实际建模中，由于有限元建立的模型是理想化的，而且在不影响精度计算的前提下，做了一些必要的简化，会造成模型的重量小于起重机的真实重量，本模型采用密度补偿法进行重量的补偿[3]。再根据实际情况，在龙门起重机大车运行机构支撑轮位置施加约束，由于模态分析中忽略外力的作用，故最终建立的有限元模型[4]见图2。

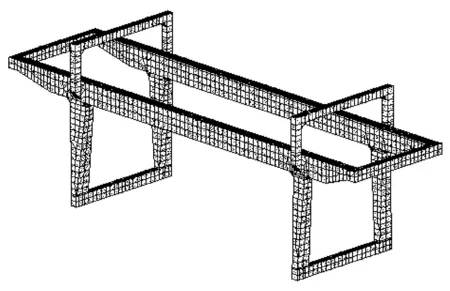
图2 龙门起重机结构模型图

3 模态计算及分析

进入ANSYS求解器，进行模态分析，得出龙门起重机结构的前十阶振型对应的频率，见表1。

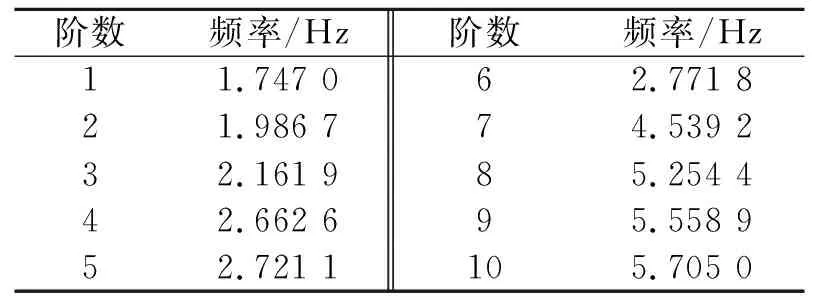
表1 前十阶频率

龙门起重机的前三阶模态分析振型见图3、4、5。

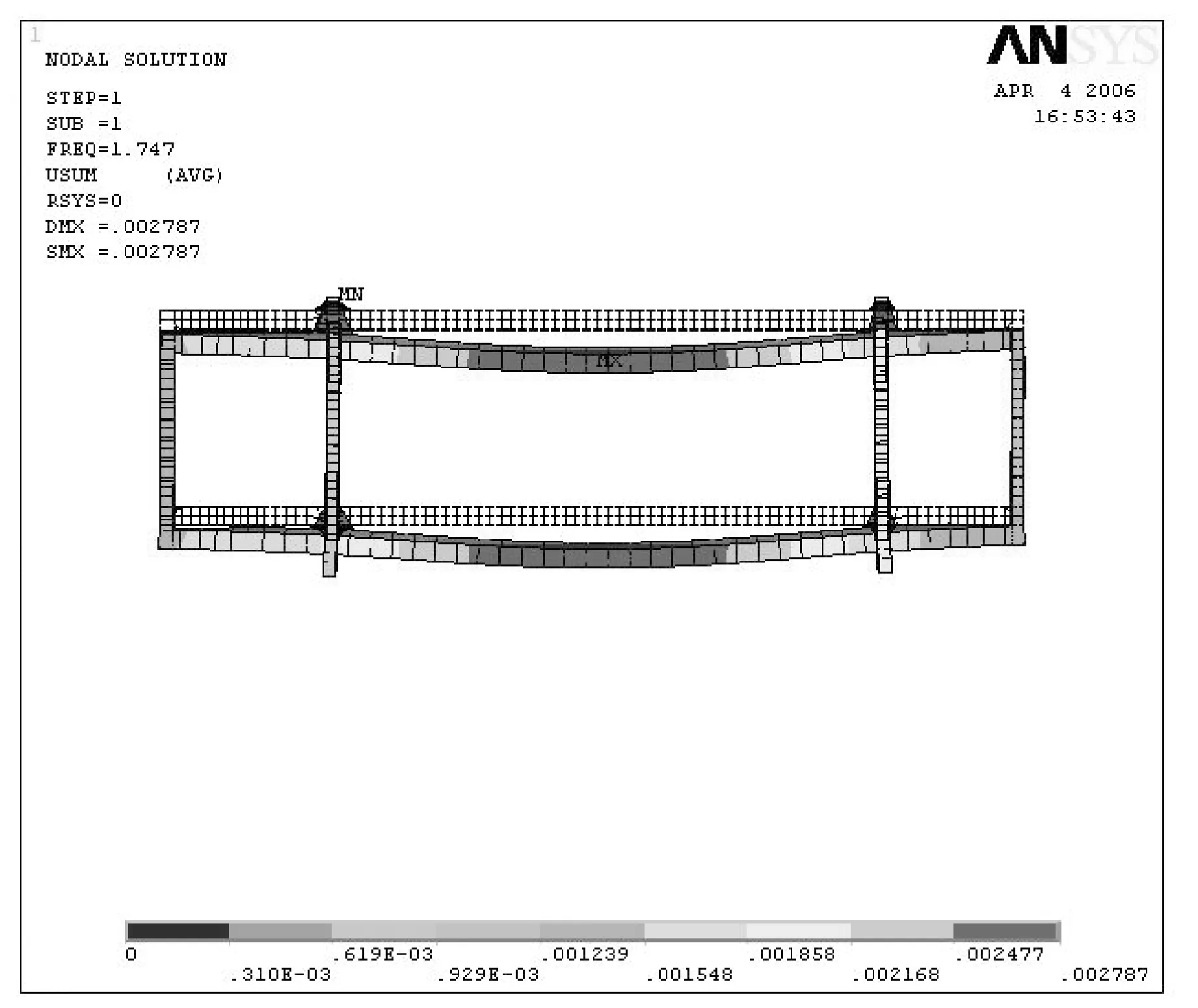
图3 第一阶振型

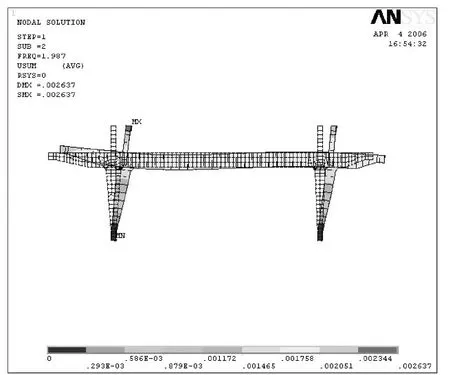
图4 第二阶振型

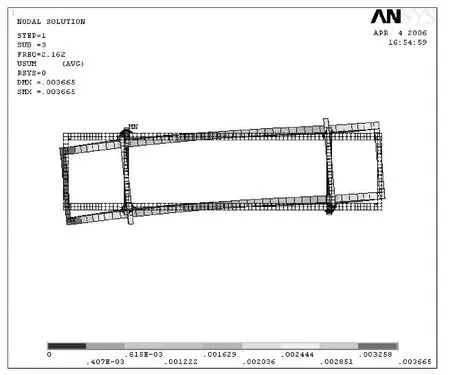
图5 第三阶振

4 模态分析

1) 分析固有频率的计算结果，由于龙门起重机结构基本对称，所以有些自振频率数值非常相近。

2) 表1中数据意味着当外部激励的频率接近表中数值时，有可能产生较大振幅，使结构受到损害，因此可通过修改设计,改变整机振动出现的频率范围,以提高操作者的舒适性。

3) 第一阶固有振型反映了龙门起重机沿轨道方向的纵向水平振动，可由大车起、制动等原因激励起振；第二阶固有振型反映了龙门起重机垂直轨道方向的横向振动，可由小车起、制动等原因激励起振；第三阶固有振型反映了沿轨道方向扭转振动。其余振型反映了龙门起重机的垂直振动及扭转，而龙门起重机的主要工作循环主要由大小车、起升机构等工作组成，主要对前几阶固有振型激励起振，其余振型不在此讨论。

在常规门式起重机的动刚度计算中，通常考虑的是垂直方向的动刚度，计算发现，龙门起重机结构的低频振动在水平方向；且龙门起重机门框结构前三阶固有频率值(水平方向)很接近，均在2 Hz左右。

图6的频率曲线反映了龙门起重机结构固有频率的走向趋势。该结论对龙门设计具有一定的参考价值，同时也可以作为其它更详细的动力学分析的起点，如瞬态动力学分析、谐响应分析、谱分析等。

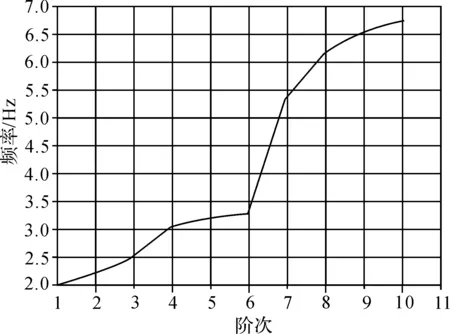
图6 频率阶次曲

5 结束语

通过对JMQ50型龙门起重机的结构分析，经过合理简化，建立了龙门起重机的有限元模型，并进行了模态分析，得到了起重机的前十阶振型和频率，不仅为此起重机结构提供具体的动载荷参数，而且更重要的是探求同类结构的共同动力学特性，对整体结构的设计质量和龙门起重机的正确运行使用提供一些有用的参考。

[1] 陈玮璋,顾迪民.起重机械金属结构[M]. 北京:人民交通出版社,1985.

[2] 杨永谦.有限元法及其在结构分析中的应用[M]. 大连：大连海运学院出版社，1992：54-168.

[3] 王 真,赵章焰.子结构技术在门座起重机门座起重机结构有限元分析中的应用[J].武汉理工大学学报：交通科学与工程版,2002，(5)：678-680.

[4] 赵汝嘉.机械结构有限元分析[M].西安:西安交通大学出版社,1990.