多种评判函数在舰艇电力系统生命力模糊评估中的应用

海军工程大学 船舶与动力学院 武汉 430033

舰船电力系统生命力是指电力系统最大限度地恢复或保持电能并使战斗设备及辅机连续工作，与战斗破损及事故破损作斗争的能力。舰艇电力系统生命力结构十分复杂，是一个多因素多层次的结构模型，因此用经典的方法达不到定量评估的目的，而模糊数学的发展为舰艇生命力的评估提供了数学工具，其中的模糊评估法就能避免这些问题。

1 舰艇电力系统生命力模糊评估模型

1.1 基本假设

仅考虑主要部件的抗损能力,并作如下基本假设。

1) 攻击武器类型: 考虑低、中、高容量(如炮弹、炸弹、导弹、鱼雷、水雷)和核武器。

2) 直接命中攻击下对主推进系统的破坏按武器对舰体的破坏半径R来考虑。

3) 根据信息论中最大熵的概念，认为武器的命中点沿舰长方向是均匀分布的。

1.2 攻击武器及其权重

攻击武器集是以影响评估对象的各种武器为元素所组成的一个普通集合，以W表示。二战以来的统计资料表明[1]，在常规武器中，对舰艇威胁较大的武器有：反舰导弹、鱼雷、非触发锚雷、沉底水雷。因此，把这4种武器作为舰艇生命力的攻击武器。

W=[W1，W2，W3，W4]

式中：W1——反舰导弹；

W2——鱼雷；

W3——非触发锚雷；

W4——沉底水雷。

上述各损伤因素的重要程度是不一样的。为了反映不同因素的重要程度，设立攻击武器的权重集S：

S=[S1，S2，S3，S4]=[ 0.40，0.35，0.15，0.10]

1.3 建立生命力等级

电力系统完好或彻底损坏是清晰可见的，但中间过渡状态复杂，具有相当大的模糊性。因此，在分析电力系统生命力时，将其分成A，B，C，D四个评判等级[2]。

A级：完全丧失生命力，电站完全损坏。

B级：基本丧失生命力，电站的供电率仅有50%,80% 以上的分区配电板损坏。

C级：具有基本生命力，电力系统供电率高于50%,尤其要保证动力、观通、导航等重要负荷的供电。

D级：具有完全生命力，电站具有100%供电能力，电力系统的供电率高于85% 以上，重要负荷不失电。

1.4 评判模型

首先确定各因素在不同武器攻击下对于不同等级的隶属关系。对于电力系统可以运用统计实验法求出电力系统处于各生命力等级的概率矩阵，也就是电力系统的模糊变换矩阵R。

式中：rij——电力系统在第i种武器攻击下处于第j损伤等级的概率。

再由各种武器的权重集S=[S1，S2，S3，S4] 可得电力系统的综合评判矩阵B=[b1，b2，b3，b4]。

B的求法可用以下几种常用的评判函数[3]得到：

1)加权平均型函数f1。

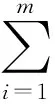
式中：W=(w1,w2, ……,wm)为归一化权向量, (x1,x2,……,xm)为任意因素集。

2)几何平均型函数f2。

3)单因素决定型函数f3。

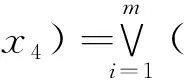
式中：W=(w1,w2, ……,wm)为正规化权向量，wi为第i个因素在综合评判中所显示的重要性的上界，此类评判中主因素起了决定性作用。其中 ∧，∨分别是[0，1]上的t-模与余模，对于任意a,b∈[0,1],

a∧b=min{a,b},a∨b=max{a,b}.

4)主因素突出型函数f4。

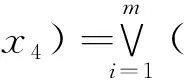
其中W= (w1,w2,……,wm)为正规化权向量，wi仍为第i个因素在综合评判中所显示的重要性的上界，但wi·xi≤wi∧xi，因此f4所得的综合评判值小于由f3所得的综合评判值，故此型函数更加“突出”了主因素起的作用。

1.5 综合评估

分别计算以上四种评估函数得到四个评判矩阵B1，B2，B3，B4再取算术平均值得：

设A,B,C,D四个评估等级的权重集为：

P=[p1,p2,p3,p4]

评估结果为系统损伤综合指标Pm：

Pm=P·BT

则系统生命力指标PS为：

PS=1-Pm

2 评估实例

下面以某艇电力系统为例[4],运用以上建立的评估模型对其生命力进行评估。运用统计实验法得到电力系统在不同武器攻击下处于各生命力等级的概率(见表1),并得到概率矩阵R。

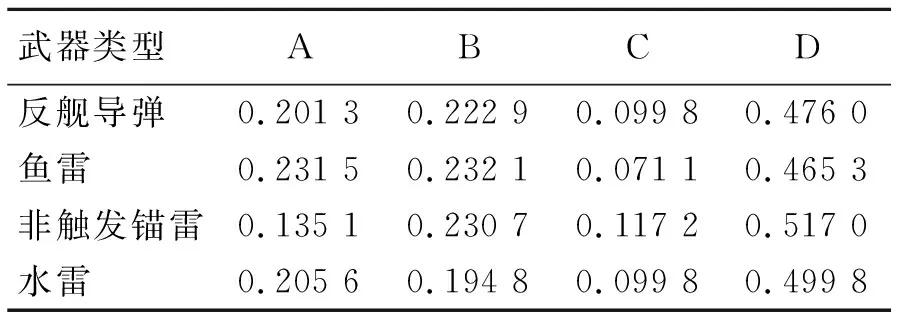
表1 不同武器攻击下电力系统处于的生命力等级概率

概率矩阵R和正规化后概率矩阵R#为：

权重集S和正规化后权重集S#为：

S=[0.40 0.35 0.15 0.10 ]

S#=[1.00 0.875, 0.375 0.25]

计算可得

B1=[0.202 4 0.224 5 0.092 3 0.480 8]

B2=[0.200 5 0.225 3 0.091 3 0.482 9]

B3=[0.223 8 0.224 4 0.102 0 0.449 8]

B4=[0.206 0 0.221 6 0.099 2 0.473 2]

取平均值

=[ 0.208 2 0.224 0 0.096 2 0.471 6]

根据有关资料设A、B、C、D四个评判等级的权重集为：

P=[0.4 0.3 0.2 0.1]

正规化后P#=[1 0.75 0.50 0.25]

则可得到系统损伤综合指标为：

Pm=P·BT

=[10.75 0.50 0.25]×

[0.208 2 0.224 0 0.096 2 0.471 6]

=0.543 8

生命力指标为:

Ps=1-Pm=1-0.543 8=0.456 2

3 结论

1) 从分析结果来看,此电力系统的损伤综合指标处于B、C 等级之间,基本可以保证舰船的电力供应。四种不同的评判函数都是系统处于D级损伤概率较大,说明了此电力系统具有较好的抗打击能力。但综合指标并不是很好,也说明了系统在设计过程中仍有需要进一步改进的地方。

2) 使用不同的评判函数得到的评判结果也不一样,为了使评判结果确能反映问题的实质，应当依据要求和上述各评估函数的意义，有所侧重的挑选合适的评判函数，必要时可以选用几种函数进行评判，然后对全部的结果再进行二次评判。

3) 根据多种武器攻击下舰艇生命力模糊综合评估模型,能把模糊性强的舰艇装备生命力指标定量化,为舰艇设备系统设计方案选优提供依据。

4) 该方法的思想和原理也可以用在其它系统的及整个舰艇的生命力的设计和论证中。

5) 该方法可直接做成计算机程序运用于各类舰艇的生命力分析。

[1] 浦金云.舰船生命力论证[D].武汉: 海军工程学院,1991：153-159.

[2] 杨树国.舰船电力系统生命力的模糊综合评判法[J].自动化技术与应用,2000(4)：25-27.

[3] 彭祖赠.孙 玉.模糊数学及其应用[M].武汉: 武汉大学出版社,2002：122-130.

[4] 浦金云,金 涛,蔡一轮.某型舰艇电力系统生命力评估报告[R].武汉:海军工程大学,2002.