穷举＋列表＝巧解

刘凤清

有些数学题的数量关系比较隐蔽，用列表方式能把条件所涉及的数量或结论的各种可能一一列出，经过筛选、比较得出结论．这样解题，可使得结论既不重复又不遗漏，反而使解题过程变得简单易行．

例１有１张伍元币，４张贰元币，８张壹元币．要拿出９元钱，可以有几种拿法？

分析：可先拿伍元币，再拿贰元币，最后拿壹元币．列表如下：

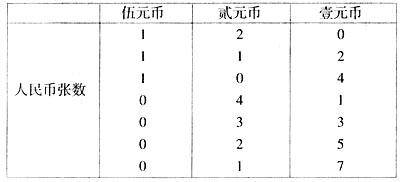
由表可知，共有７种拿法．

例２从１到１００这１００个自然数中，每次取出２个，要求它们的和大于１００，有多少种取法？

分析：若每次取出的两个数中，较大的数为５０或５０以下的数，则不符合条件．

把符合条件的取法列表如下：

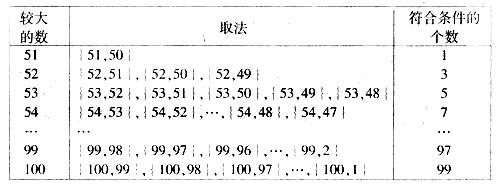
符合条件的取法有１＋３＋５＋７＋…＋９７＋９９＝２ ５００（种）．

例３把１００分成四个数，第一个数加上４，第二个数减去４，第三个数乘以４，第四个数除以４，结果恰好相等．求这四个数各是多少？

分析：由第三个数乘以４可知最后结果应是４的倍数，故最后结果应在４，８，１２，１６，２０，２４这六个数之中，然后再检验所分成的四个数之和是否为１００．

依题意列表如下：

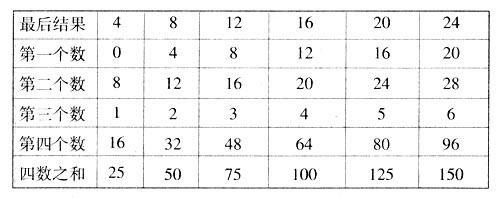
例４某公共汽车线路上共有１５个车站（包括起点站和终点站）．公共汽车在从起点站到终点站的行驶过程中，每一站（包括起点站）上车的人恰好在以后的各站都各有１人下车．要使汽车在行驶中乘客都有座位，那么在车上至少要安排多少个座位？

分析：只需求车上最多有多少人即可．依题意列表如下：

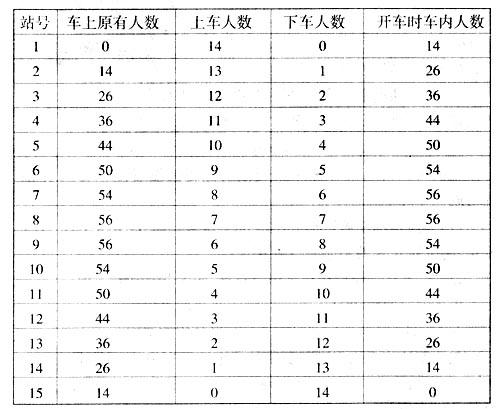
通过比较表中各数据可知，在第７站和第８站开车时，车内乘客最多，有５６位，所以车上至少要安排５６个座位．