从一题多解到一题多变,提升学生的关键能力——以求三角形面积或周长的范围为例

邓成兵

(四川省成都市航天中学校)

《普通高中数学课程标准(2017版2020年修订)》中提出,高中数学教学应该以发展学生数学核心素养为导向,通过数学解题教学去落实“四基”“四能”,引导学生把握数学内容的本质,达到学生用科学方法分析问题、解决问题,才有利于引导学生将其转化为自己的思维方式,实现这一目标,需要提升学生的关键能力,借此笔者就以一题多解到一题多变为例,提升学生的关键能力与大家交流.

一、概念界定

数学关键能力:指在数学情境中发生在较高认知水平层次上的,为达到某种特定目标或完成某项任务而付诸努力的一种综合性能力,包括问题分析解决能力、数学知识应用能力、创造力和批判性思维能力等.

一题多解指运用不同的思维方式,从不同角度来解答同一道题的思考方法.经常进行一题多解的训练,能从多种解法的对比中优选最佳解法,总结解题规律,寻找创造性的解题方法,有益于学生解题技巧的形成和能力的提高,从而提升学生批判思维、创造性思维和自主学习能力等.

一题多变是指变换题目的条件或结论,变换题目的形式,或者将某项条件与结论交换等,而题目所考查的实质不变,变化的目的是从不同角度、不同方向揭示题目的本质.通过一题多变,让学生在变化中总结解题方法,从变化中发现规律,从变中发现“不变”,从而解决一类问题,遏制“题海战术”,从而提升学生创新能力、逻辑思维能力和举一反三能力等.

二、案例分析

一题多解,培养学生求异创新的发散思维.通过一题多解的训练,学生可以从多角度、多途径解决问题的方法,拓展解题思路.

学生在学习数学和运用数学解决问题时,不断地经历直观感知、观察发现、归纳类比、空间想象、抽象概况、符号表示、运算求解、数据处理、演绎证明、反思与建构等思维过程.一题多解,可以帮助学生学会多角度分析和解决问题,提高学生的数学能力和非认知能力.下面以2023·四川石室中学高考适用性考试(一)第14题为例,通过“一题多解”探究如何提升学生的关键能力.

【题目呈现】(2023·四川石室中学高考适用性考试(一)·14)在△ABC中内角A,B,C对边分别为a,b,c,若b+2cosB+bcosA=6,a=2,求S△ABC最大值.

【分析】本题属于传统题,利用余弦射影定理把acosB+bcosA转化为c,得到两边的和与第三边,利用余弦定理+基本不等式或转化为椭圆的第一定义求解.

2.1 题之一问,问之一解

解：把a=2代入b+2cosB+bcosA=6,由余弦射影定理可得:b+c=6.

解法一:余弦定理+基本不等式

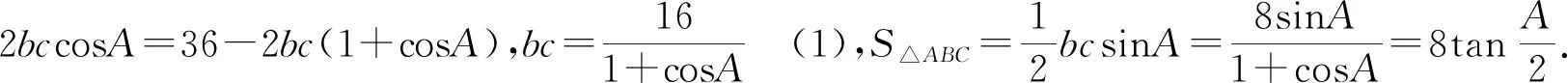
解法二:海伦公式+基本不等式

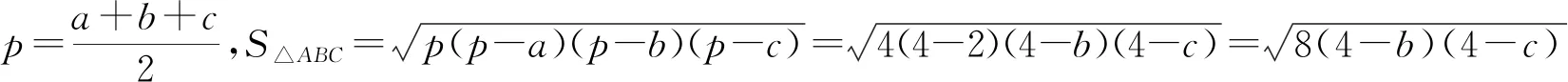
解法三:类比化归思想

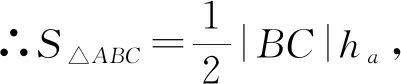
【评析】解法一利用余弦定理构造方程,用∠A表示bc,代入三角形面积第二公式,S△ABC转化关于∠A的三角函数,最后利用三角函数的有界性进行求解;解法二利用海伦公式+基本不等式进行求解;解法三利用类比化归思想,发现b+c=AC+AB=6>BC=2恰好满足椭圆的第一定义(数形结合),再结合椭圆的焦点三角形求面积的最大值,动点A运动到短轴的端点处时有最值.从三种解法发现:解法二利用海伦公式求三角形的面积,在高中阶段没作要求;解法三利用椭圆的第一定义求解,但绝大部分同学难以想到;解法一利用余弦定理、三角函数进行求解,虽然运算量大,但解法一是求有关三角形问题的常规解法;所以,求三角形有关面积或周长的范围或值,有两种途径:

(1)利用正、余弦定理把边转化为角,利用三角函数进行求解;(2)数形结合求解.

著名数学家波利亚说过这样一句话:“掌握数学也就意味着要善于解题.”如何挖掘题目的内涵和价值呢?笔者认为可以借助思维导图来完成.这对进一步提高学生的解题能力,完善学生的认知结构有着重要作用.如本题可以画出它的思维导图,如图所示:

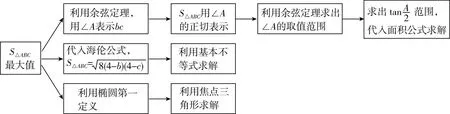
通过一题多解,让学生从不同的角度思考问题,得到多种解题思路,更好地理解数学知识,增强解题能力,还能培养学生的创造思维能力.为了更好地培养学生的发散思维能力,增强学生数学应用能力和提高数学解题能力,需要积极开展“型异质同”或“型近质同”题目的训练——一题多变.例如把上题中的条件改为已知一边与一角或两边,如何求三角形面积或周长的范围呢?

2.2 解之一变,变之一通

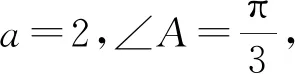
解法一：余弦定理+基本不等式

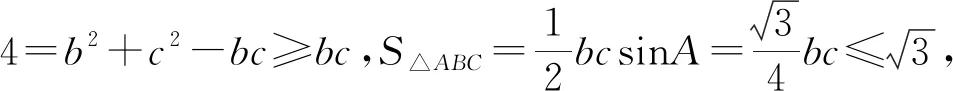
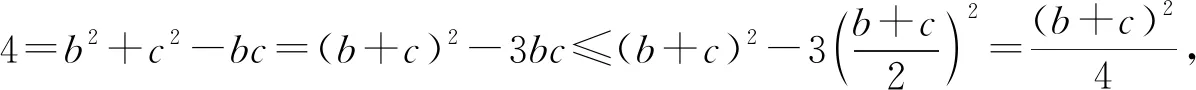
解法二：正弦定理+三角恒等变换

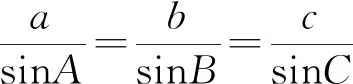
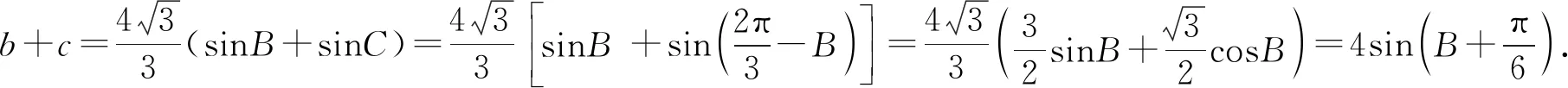
【点评】解法一主要利用余弦定理+基本不等式求三角形的面积和周长的范围,求解过程比较容易,易错点为漏掉三角形两边之和大于第三边这一隐含条件,从而得到错误答案(2,6];解法二主要利用正弦定理+三角恒等变换,这种方法是求三角形面积和周长的通解通法,思路比较清晰,但解题过程比较烦琐.如果把△ABC改为锐角三角形,其他条件不变,求三角形的面积和周长的范围时,上面两种方法都能用吗?为什么呢?

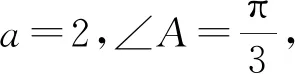
【分析】如果△ABC为锐角三角形,利用余弦定理+基本不等式求解,整个求解过程中,无法体现此三角形是锐角三角形,所以只能利用正弦定理+三角恒等变换求解.

解法一：正弦定理+三角恒等变换

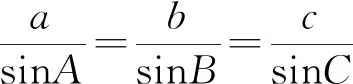
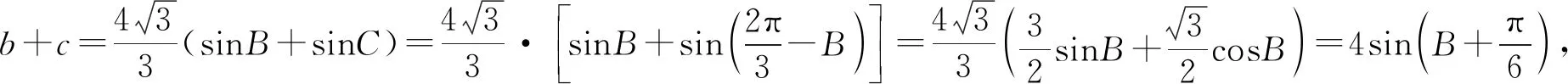
解法二：数形结合

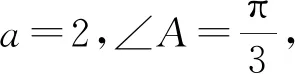
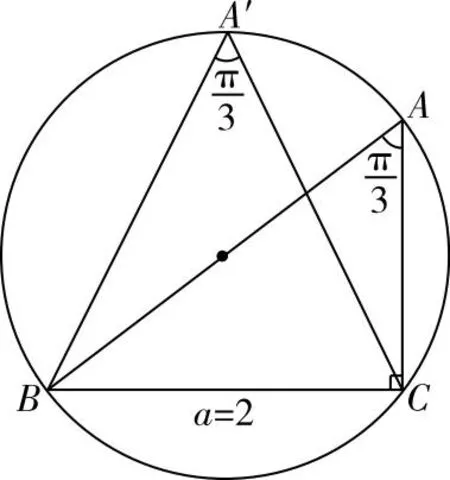
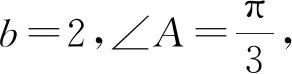
解法一：正弦定理+三角恒等变换

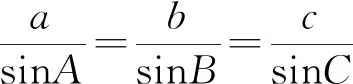
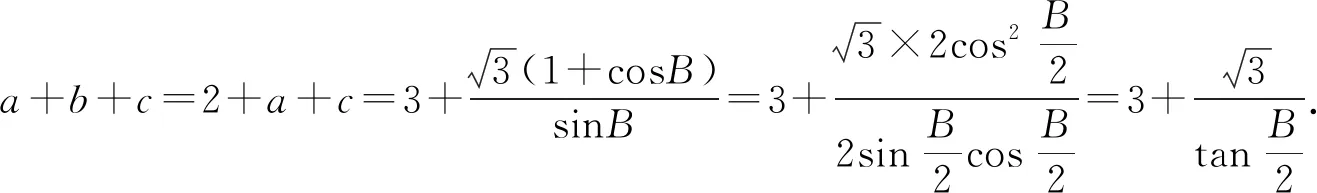
解法二：数形结合

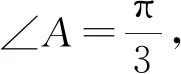
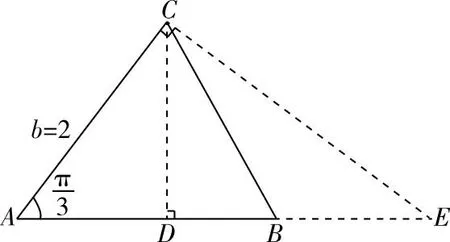
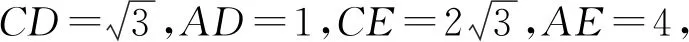
【变式4】在锐角△ABC的内角A、B、C对边分别为a、b、c,若b=2,a=3,求△ABC面积与周长的取值范围.

解法一：余弦定理+极限思想

解法二：数形结合

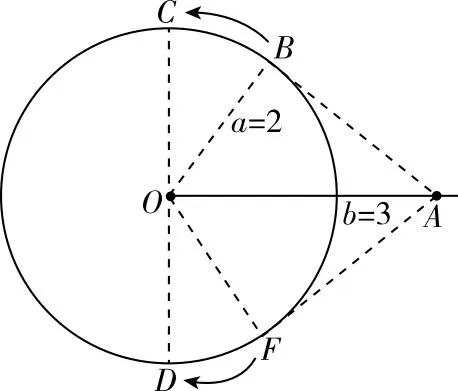
通过上面一题多变发现,如果知道锐角三角形的一边一角或两边,可以求出此三角形的面积与周长的范围,有两种思路:思路一:利用正、余弦定理把边转化为角,利用三角函数进行求解,此方法是通解通法,求解时一定要注意所求解角的取值范围;思路二:数形结合,此方法高效,省时省力对学生的关键能力要比较高;当然,若是钝角三角形,已知一边与一角、两边求其面积或周长的取值范围,其解法与锐角三角形对应的解法相似.

三、教学反思

“一题多解与一题多变”的教学方法,有助于调动学生思维和行动的积极性,主动参与知识方法和系统的构建,启发学生自主分析、思考,逐步引导学生从简单到复杂的途径来拓展知识视野,增强获取知识的能力,激发创新思维.教师在教学中不仅要善于引导学生发现问题,而且要善于帮助学生学会及时归纳、总结、提炼,解决问题的过程实际上就是寻求认识问题的正确途径,使学生分析、综合、评价能力得以逐步提高,实现由“解题”向“解决问题”的转变;帮助学生提升数学关键能力.