Geometric phase under the Unruh effect with intermediate statistics

Jun Feng(冯俊), Jing-Jun Zhang(张精俊), and Qianyi Zhang(张倩怡)

School of Physics,Xi’an Jiaotong University,Xi’an 710049,China

Keywords: open quantum system,geometric phase,Unruh effect

1. Introduction

A quantum system can acquire the memory of its undergoing quantum evolution in the form of a phase factor. The history of this geometric phase(GP)concept has undergone a long history, back to early Pancharatnam’s classical notion[1]and Aharonov–Bohm effect.[2]The general form of geometric phase was firstly introduced by Berry in the adiabatic and cyclic unitary evolution of non-degenerate states.[3]Later,numerous generalizations[4–6]have included nonadiabatic, noncyclic and nonunitary evolution, also for degenerate states.Due to its geometric origin from the holonomy of states’line bundle,[7]GP is robust against certain uncontrolled fluctuations, thus promising a holonomic quantum computation under realistic physical conditions.[8]As an important feature of quantum system, GP has fruitful applications in diverse fields, such as molecular dynamics[9]and electron transport in materials.[10]Experimentally, GP has been tested in various platforms,including the system with photons[11]and with neutrons.[12]

In a realistic world, quantum systems inevitably suffer a decoherence or dissipation resulting from the interaction between the systems and the environment. Thus, it is of great importance to generalize the GP of pure state to quantum open systems and for mixed states. The extension to a mixed-state-GP was firstly proposed in Ref. [13] in a purely mathematical fashion of purification. Based on an interferometric interpretation or kinematic approach,Sj¨oqvistet al.[14]introduced an alternative definition of GP for nondegenerate density matrix,which was soon generalized to degenerate mixed states in Ref. [15]. For nonunitary quantum evolution, Tonget al.[16]considered an arbitrary reduced dynamics of an open quantum system and proposed a gauge invariant GP which in principle can be experimentally tested in interferometry.[17]

In recent years, there is a growing interest in using the GP as a quantum probe of sensitive relativistic effects. In these regimes, the relativistic effects like the Unruh effect and Hawking radiation are in general considered as an environment decoherence.[18]Along this line, many efforts focus on using mixed-state-GP as an efficient thermometer of aforementioned effects have been made. For instance,Mart´ın-Mart´ınezet al.[19]examined the GP of an accelerated Unruh–DeWitt(UDW)detector which couples to a single-mode scalar background engineered in a cavity. They claimed that the Unruh effect, i.e., an accelerating detector perceives a thermal radiation originated from random fluctuations in vacuum,may cause a detectable modification on the GP comparing to a static case. In Ref.[20],a similar variation of the GP for a detector coupled to an electromagnetic field has been evaluated.Inspired from Bell and Leinaas’insight[21]that the Unruh effect could easier be experimentally achieved through a circular motion,Jinet al.[22]considered a circularly accelerated atom coupled to a bath of fluctuating electromagnetic fields. They showed that the atom can acquire a larger GP than that with linear acceleration once properly selecting the initial state.

Besides its metrological advantages, the GP may also sheds a light on the observer-dependent nature of quantum fields in curved spacetime, and provides an important probe on the quantum nature of vacuum fluctuations as well as the spacetime structure. For instance, in a background of Schwarzschild black hole, it was shown[23]that the GP of a hovering UDW detector would be affected by the spacetime curvature. The thermal nature of Hawking effect is encoded in an outgoing flux of radiation which can be manifested by a modification on the GP of the detector comparing to that in flat spacetime. In the same regime, other geometric objects such as Aharonov–Anandan invariant and its relation to entanglement witness have been studied in Ref. [24]. In a cosmological paradigm, the freely falling detector would perceive a correction on its GP[25]ascribed to a Hawking-type radiation from cosmological horizon,and reveals the curvature structure of de Sitter space.In a stationary and axisymmetric spacetime,the GP of a static detector reveals[26]the Hawking effect from the Kerr black hole by its correction as opposed to that in a flat spacetime.

In this paper,we will study the GP undergoing the Unruh effect of an accelerating UDW detector, which interacts with a conformal background field inn-dimensional Minkowski spacetime. Beyond common studies on the Unruh effect with Planckian distribution, our detector model will exhibit a response spectrum of intermediate statistics analogue to(1+1)-dimensional anyon field.[27]This generalization would include Takagi’s statistics inversion as a special case,[28]which claimed[29]that the response spectrum of the detector has an interchange between Bose–Einstein and Fermi–Dirac distributions for varying spacetime dimension. This is viewed[30]as a local feature of the detector,encoding the different thermalizing paths for the detector to approach its equilibrium. Our aim is to manifest the thermality and quantum nature of the Unruh effect with such general statistics by its modification on the GP of the detector’s evolving state. We will treat the UDW detector as an open quantum system whose reduced dynamics is governed by a Lindblad-type master equation.[31]Its Markovian evolution can then be resolved for time much longer than the thermalization time.[32]We will calculate the GP for the accelerating detector undergoing an Unruh noise.By comparing the results with the case of inertial motion, as well as the GP of an inertial detector immersing in a thermal bath, we will show that various features of the Unruh effect can be manifested by the non-trivial GP of the accelerating UDW detector:

1)The GP of the detector is a function on the Unruh temperature essentially characterizing the thermalization nature of the Unruh effect.Moreover,the GP also depends on detector’s local features,e.g.,its device design and background coupling.Therefore the GP can also manifest the different thermalizing paths, i.e., the ways for the detector approaching its thermal equilibrium.

2) Comparing to an inertial detector, the GP for the accelerating detector gets a modification due to the Unruh effect. For a general conformal background,we show that such modification depends on the scaling dimension of the field,thus can distinguish the intermediate statistics of detector’s response spectrum.

3) The difference between the GP undergoing an Unruh radiation and that for a static observer immersing in a thermal bath will be estimated for arbitrary dimensional Minkowski spacetime.We find that the difference of the GP in two scenarios depends on the spacetime dimensionality,which manifests that the Unruh effect has intrinsic quantum nature rather than merely a thermal noise.

We would like to argue that although the first and third points have been investigated recently in Ref. [30] by using the standard excitation spectrum of an UDW detector,the GP may provides a more refine probe beyond the detector’s response. For example, we would demonstrate that the statistics inversion exhibiting in the response spectrum is spoiled in terms of the GP.This is consistent with our previous work[33]and endows the GP a role of quantum probe of the Unruh effect which is irrelevant with spurious interchange of statistics encoded in the functional form of response function.[30]

Throughout the paper, we admit the natural units as ¯h=c=kB=1.

2. Atom evolution with a conformal background

2.1. The setting

We consider the combined system of detector and background field having a total Hamiltonian

For a weak coupling between the detector and the external field(μ ≪1),and writing the initial state as(Born approximation)ρtot(0)=ρ(0)⊗|0〉〈0|, whereρ(0) is the initial state of the detector and|0〉is the field vacuum in comoving frame, the dynamics of the UDW detector can then be obtained by integrating over the background field degrees fromρtot(τ),which gives an integro-differential master equation as[36]

2.2. Detector’s state with intermediate statistics

To derive the complete dynamics of detector’s state (7),we need to specify the Kossakowski coefficientsγ±following an accelerating trajectory of atom,like

which contains a Bose–Einstein or Fermi–Dirac factor modulated by a polynomial ofω. It is interesting to note that once the scaling dimension happens to be selected asΔ=(n-2)/2,these frequency Wightman functions just coincide with Takagi’s statistics inversion for different spacetime dimensionality. Therefore,for genericΔ,Eq.(13)exhibits an intermediate statistics as a continuously interpolation between the Bose–Einstein and Fermi–Dirac statistics.

3. GP of an accelerating UDW detector

The accelerating UDW detector evolves nonunitarily due to the Unruh decoherence from its coupling to the conformal background.Given an initial pure state,the detector eventually arrives a Gibbs mixed state after sufficient long time. During the evolution,the detector would acquire a nontrivial phase.

3.1. GP of the detector undergoing nonunitary evolution

3.2. GP with intermediate statistics

Inserting the Kossakowski coefficients for the conformal background (17) into Eq. (25), we know that the geometric phaseΦUnruh(ω,TU,θ,Δ) should be a function of detector’s energy spacingω,the Unruh temperatureTUis proportional to accelerationa,the initial state parameterized byθ,as well as the scaling dimensionΔof conformal background.As pointed in Ref.[20],for a weak coupling to the background,the Lamb shift terms in GP(25)can be omitted,since it only contributes to the phase at higher orders. This means that one can conduct the numerically estimation on the phaseΦUnruhwith admittingΩ ≈ωin the analysis.

Previous studies clarified[39]that the thermal nature of the Unruh effect essentially guaranteed by thermalization theorem is characterized by the Unruh temperatureTU. The detector’s local features,e.g.,its device design and background coupling,should determine the different thermalizing paths, i.e., the way for the detector approaching its thermal equilibrium.[30]Hereby, we manifest various features of the Unruh effect by the GP of the detector.

For varying initial state preparation,it is easy to see from Eq. (25) that the related GP is periodic on the initial state parameterθ. In Fig. 1(a), we depict theΦUnruhas a function of the Unruh temperatureTUfor a periodθ ∈[0,2π),while the conformal background is selected with scaling dimensionΔ=0.5. One can observe that with growing Unruh temperatureTU, the absolute value of the phase degrades monotonously.On the other hand,while the atom frequencyωmostly appears in a combined form with Unruh temperature asω/TU,we expect that the largerωcan roughly be regarded as lower temperature,thus enhance the absolute value ofΦUnruh.

With varying scaling dimensionΔ,the detector exhibits a response spectrum with an intermediate statistics. In Fig.1(b),we illustrate theΦUnruhas a function both on the Unruh temperature and the choice of conformal scaling dimension. In particular,the GP has distinct behavior under larger Unruh decoherence for different choices ofΔ. For instance,around the rangeΔ ∈(0,1), theΦUnruhis a monotonic increasing function, while degrading with growing Unruh temperature forΔ ＞1. In this sense, we suggest that the behavior of the GP under the Unruh effect can distinguish the detector’s apparent statistics, encoding the different thermalizing path of the detector.

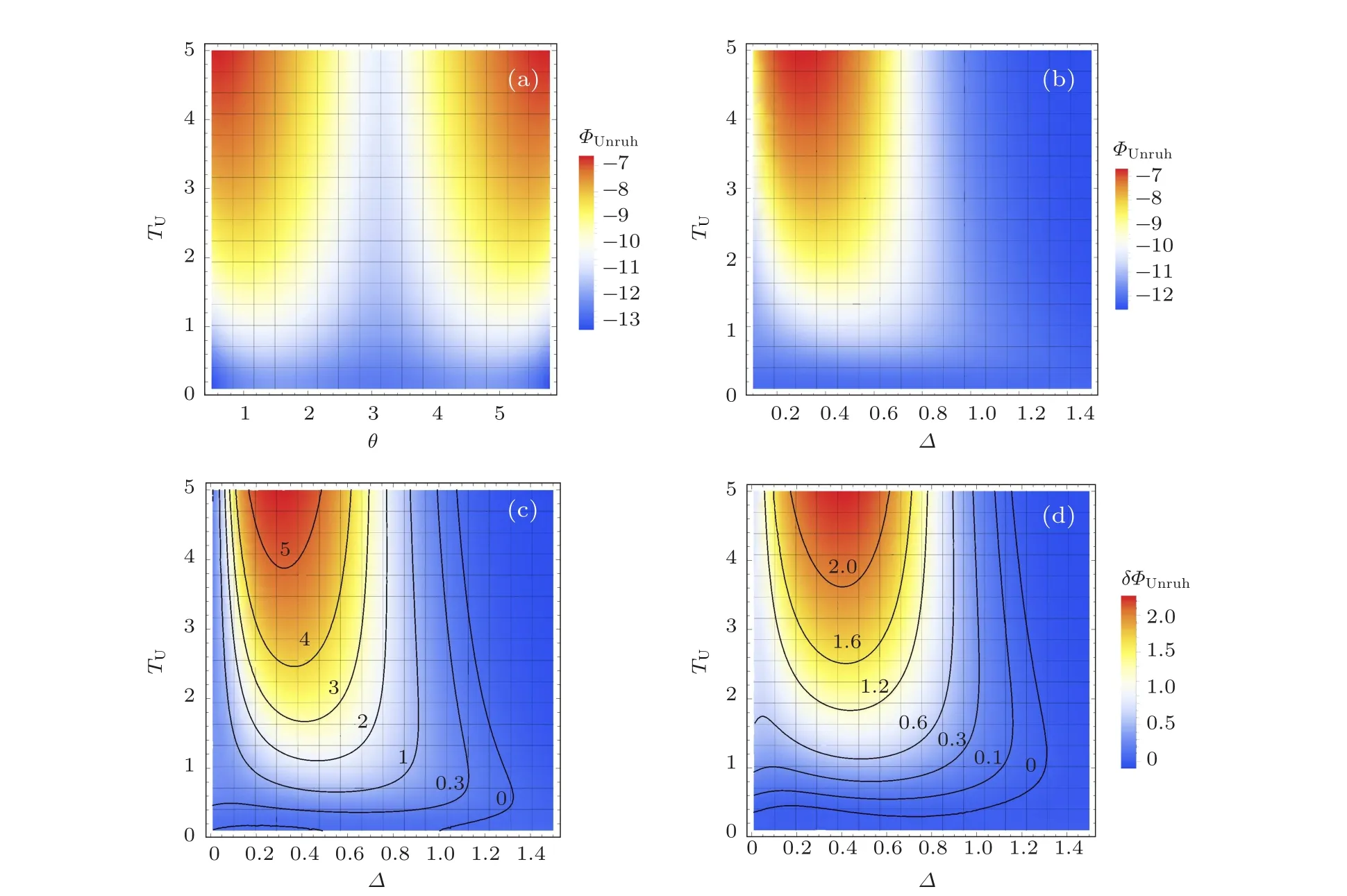
Fig. 1. (a) The GP as a function of the Unruh temperature TU and the initial state parameter θ. The estimation is made with choosing ω =1,Δ =0.5. (b)The GP as a function of the Unruh temperature TU and scaling dimension Δ of conformal background. The estimation is made with choosing ω =1, θ =π/2. The modification of GP due to the Unruh effect is demonstrated as a function of the Unruh temperature and scaling dimension of background field. The estimation is made with choosing θ =π/2 and(c)ω =1(d)ω =2.

However, with a selection of the scaling dimension asΔ=(n-2)/2,comparing the GP evolution and detector’s response (15), a crucial difference between our result and detector’s response function needs to be highlighted, i.e, no inversion behavior of GP as a function of dimensionality can be found. This is consistent with our previous work[33]and indicates that GP is a quantum probe essentially distinguishing the ways of the detector thermalizing,which is irrelevant with spurious interchange of statistics encoded in the functional form of the response function.[30]

We are further interested in the modification on the GP originated from the Unruh effect. For this purpose, we compare the GP of accelerating detector to that in an inertial frame,and define the difference of GP in two scenarios as

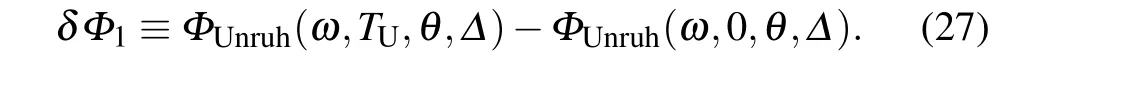
Without loss of generality,we numerically estimate this phase difference for the initial state prepared withθ=π/2, as depicted in Figs.1(c)and 1(d), Besides the Unruh temperature,we observe that the modification of GP from the Unruh effect also depends on the choice of scaling dimension of background field. Since the detector exhibits a response spectrum labeled byΔ,the phase differenceδΦ1resulted from the Unruh effect then can manifest the intermediate statistics of the local response.

Essentially,the Unruh radiation is different from the thermal noise observed by an inertial detector immersing in a thermal bath, which has clearly been demonstrated by aforementioned statistics inversion that is absence for a thermal bath.In the present stage, we expect to manifest such difference by comparing the GP related to two scenarios. Consider a static detector immersing in a thermal bath inn-dimensional Minkowski spacetime with temperatureT0. The related Kossakowski coefficients can be derived from Eqs. (6) and (16)as Substituting these coefficients into Eq.(25),we can obtain the GP related to a thermal bathΦthermal(ω,T0,θ,n), a function of atom’s energy spacingω, bath temperatureT0, initial state preparation and spacetime dimensionalityn.

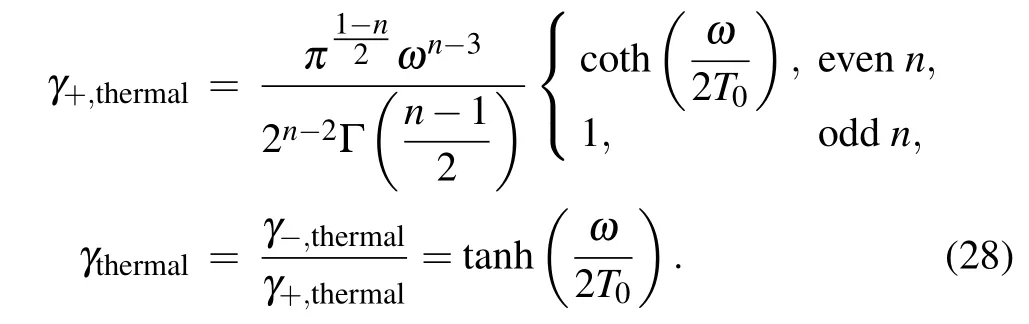
In Figs. 2(a) and 2(b), we illustrate the GP related to a thermal bathΦthermalfor different spacetime dimensions,i.e.,n=3,4.We note thatΦthermalhas similar behavior under varying initial states or thermal bath temperature. This is not surprising since the response of a static detector to a thermal bath always exhibits a Planck form in arbitrary dimensional flat spacetime. This implies that all thermalizing paths for such detector are essential identical,which can not be distinguished by the GP.

Fig.2. The GP related to a thermal bath Φthermal is estimated in(a)n=3 and(b)n=4 Minkowksi spacetime,as a function of bath temperature T0 and initial state θ. The phase difference δΦ2 distinguishing the Unruh radiation and a thermal noise is estimated,as a function of bath temperature T0 and initial state θ,with(c)n=3 and Δ =0.5,(d)n=4 and Δ =1. Throughout the estimation,the scaling dimension is chosen like Δ =n/2-1,while ω =1 is fixed.

However, our purpose is to recognize the difference between Unruh radiation and thermal noise by their related GP.Therefore,we define another phase difference as

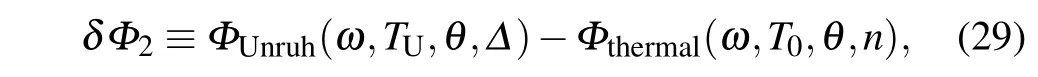
withTU=T0,and a selection of scaling dimensionΔ=n/2-1 should be made. As an example,we estimate this phase differenceδΦ2for the UDW detector(with energy spacingω=1)inn=3 (identify toΔ=0.5) andn=4 (identify toΔ=1)dimensional spacetime in Figs.2(c)and 2(d), respectively. It clearly demonstrates that an asymmetry on the GP under the effects of the Unruh and thermal background exists, which convinces that an Unruh radiation is essentially different from a noise from thermal background. Another interesting thing is that while theΦthermalremains a similar function behavior for arbitraryn, the phase differenceδΦ2definitely distinguishes the spacetime dimensionality. This is another demonstration on the ability of the GP to distinguish the paths of the thermalization for accelerating UDW detector.

4. Summary and discussion

In this paper,following an approach of open quantum system, we investigate the GP acquired through the nonunitary evolution of an accelerating UDW detector inn-dimensional spacetime. Beyond the conventional scalar or fermionic background, we consider the detector coupling to a conformal background field with intrinsic positive scaling dimensionΔ,which exhibits a spectrum with intermediate statistics coinciding with a(1+1)anyon field. We find that comparing to the model with an inertial detector,the related GP for accelerating detector gets a nontrivial modification depending on the Unruh temperature that characterizes the thermalization nature of the Unruh effect. Moreover, with varying scaling dimensionΔ,the GP of the detector can distinguish the different thermalizing paths corresponding to intermediate statistics. By comparing the GP of accelerating detector to that of a thermal bath in static frame,we show that the perceived radiation in Unruh effect is essentially different from a radiation noise observed by a static detector immersing in a thermal bath. Therefore,from the view of geometric phase, we convince the quantum origin of the Unruh effect which can not merely be a thermal noise.

We would like to mention that the perspective on the Unruh effect with the tool of GP adopted in the present paper provides a complement to previous studies,and agrees on the thermality and quantum features of the Unruh effect revealed by other quantum probes, e.g., response function,[30]Fisher information[33]or entropic monotone of quantum coherence.[40]It would be interesting to extend the present analysis to multi-UDW detectors system and compare the GP behavior with other quantum probes.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 12075178) and Natural Science Basic Research Plan in Shaanxi Province of China (Grant No.2018JM1049).